
never forget 5.1红外光谱概述 how to aream 4.红外光谱的特点 (1)依据样品吸收谱带的位置、强度、形状、个数,推测分子 中某种官能团或化学键的存在与否,推测官能团的邻近基团,确 定化合物结构 (2)不破坏样品, 对任何样品的存在状态都适用,如气体、液 体、可研细的固体或薄膜似的固体都可以分析,测定方便,制样 简单 (3)特征性高。对不同结构的化合物可给出特征性的谱图,也 叫“分子指纹光谱” (4)分析时间短。普通红外光谱做一个样可在10分钟内完成, 傅里叶变换红外光谱仪一秒钟以内就可完成扫描 (5)样品用量少,可回收。一次约1-5mg,甚至几十微克 (6)方便与其它类型仪器联用,进行多组分分析 6
4. 红外光谱的特点 6 (1)依据样品吸收谱带的位置、强度、形状、个数,推测分子 中某种官能团或化学键的存在与否,推测官能团的邻近基团,确 定化合物结构 (2) 不破坏样品,对任何样品的存在状态都适用,如气体、液 体、可研细的固体或薄膜似的固体都可以分析,测定方便,制样 简单 (3)特征性高。对不同结构的化合物可给出特征性的谱图,也 叫“分子指纹光谱” (4)分析时间短。普通红外光谱做一个样可在10分钟内完成, 傅里叶变换红外光谱仪一秒钟以内就可完成扫描 (5)样品用量少,可回收。一次约1-5mg,甚至几十微克 (6)方便与其它类型仪器联用,进行多组分分析 5.1 红外光谱概述

never forget 5.1红外光谱概述 how to aream 5.红外光谱的应用 定性: 与紫外、核磁、质谱相结合,解析 材料的分子结构。 定量: 依据特征峰的强度,朗伯一比尔定律 7
5. 红外光谱的应用 7 定性: 与紫外、核磁、质谱相结合,解析 材料的分子结构。 定量: 依据特征峰的强度,朗伯-比尔定律 5.1 红外光谱概述
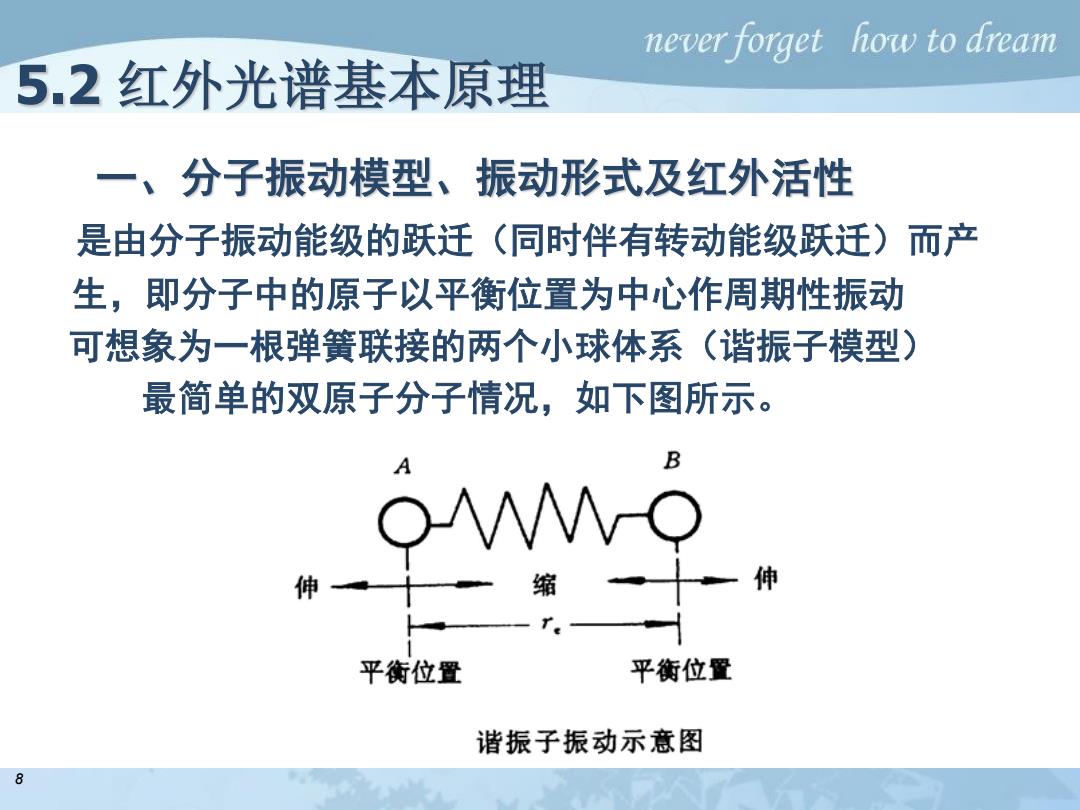
never forget how to dream 5.2红外光谱基本原理 一、分子振动模型、振动形式及红外活性 是由分子振动能级的跃迁(同时伴有转动能级跃迁)而产 生,即分子中的原子以平衡位置为中心作周期性振动 可想象为一根弹簧联接的两个小球体系(谐振子模型) 最简单的双原子分子情况,如下图所示。 B 缩 伸 平衡位置 平衡位置 谐振子振动示意图 8
一、分子振动模型、振动形式及红外活性 是由分子振动能级的跃迁(同时伴有转动能级跃迁)而产 生,即分子中的原子以平衡位置为中心作周期性振动 可想象为一根弹簧联接的两个小球体系(谐振子模型) 最简单的双原子分子情况,如下图所示。 5.2 红外光谱基本原理 8

5.2红外光谱基本原理 never forget T how to aream 1、双原子分子振动方程式 根据虎克定律: h K 2π k--化学键的力常数(Ncm),与键能和键长有关; --双原子的折合质量:μ=m1m2/(m1+m2) M是折合相对原子质量 分子的振动能级(量子化): E振(+l/2)hv ν:化学键的振动频率; V:振动量子数(V=0、1、2.…),当V=0时,E0,称为零点能。 9
1、双原子分子振动方程式 分子的振动能级(量子化): E振动=(V+1/2)hν ν:化学键的振动频率; V: 振动量子数(V=0、1、2......),当V=0时,E≠0,称为零点能。 根据虎克定律: k-----化学键的力常数(N/cm) ,与键能和键长有关; μ---双原子的折合质量: μ =m1m2/(m1+m2 ) 5.2 红外光谱基本原理 𝑣 − (cm−1) = 1 λ = 1 2π𝐶 𝑘 μ = 130𝟑 𝑘 M 9 M是折合相对原子质量

5,2红外光谱基本原理 never forget 7 how to aream 任意两个能级间的能量差为: h K E=△VIhv=△V 2元 当△V=1时,0→1振动能级的跃迁,称为基本振动频率 或基频吸收带。 折合质量和键力常数是影响基本振动频率的直接因素。 K越大,或μ越小,或化学键的振动频率越高,吸收峰 将出现在高波数区;反之,则出现在低波数区。 10
任意两个能级间的能量差为: κ 2 h E = Vhv = V π μ 当△V =1时,0→ 1振动能级的跃迁,称为基本振动频率 或基频吸收带。 折合质量和键力常数是影响基本振动频率的直接因素。 K 越大,或μ越小,或化学键的振动频率越高,吸收峰 将出现在高波数区;反之,则出现在低波数区。 h 5.2 红外光谱基本原理 10