
这里会给一些具体例子来推导一个简单的洛伦兹变换。需要说明的是,这个推导过程并不具有十分严格的 意义,只是让大家能够从物理含义上看出洛伦兹变换是怎么回事。 首先,我们要给出狭义相对论的两个基本假设: 1、相对性原理。 2、光速不变原理。 所谓相对性原理指的是一个原则,物理规律在不同的惯性参照系中,有相同的数学形式。关于这个原理, 在我们这次推导过程中并没有显著地用到,这里就一笔带过吧。 这里要详细说一下光速不变原理。 光速不变原理的一个通俗的解释就是:光在任何惯性系中都有相同的速率。 这个解释其实和我们的日常生活是有尖锐矛盾的,下面我们通过例子来详细体会一下这种矛盾到底尖锐到 什么程度。 我们设想一个场景:A和B两个人,A静止在地面上,A用一把枪瞄准了B,在某时刻开了一枪,B在子 弹出膛的瞬间以一个恒定的速度逃跑。我们知道,如果B逃跑的速度非常快,要是和子弹速度一样的话, 子弹是追不上B的,看下图。 A和B站在地面上,相距10米 b米 10米 距离 A对着B射击,B敝腿就随 0米 10米 距离 10米 B跑动的速度达到子弹的速度的话,B和子弹一直相距10米 o米 10米 距离 4米 :14米 10米
这里会给一些具体例子来推导一个简单的洛伦兹变换。需要说明的是,这个推导过程并不具有十分严格的 意义,只是让大家能够从物理含义上看出洛伦兹变换是怎么回事。 首先,我们要给出狭义相对论的两个基本假设: 1、相对性原理。 2、光速不变原理。 所谓相对性原理指的是一个原则,物理规律在不同的惯性参照系中,有相同的数学形式。关于这个原理, 在我们这次推导过程中并没有显著地用到,这里就一笔带过吧。 这里要详细说一下光速不变原理。 光速不变原理的一个通俗的解释就是:光在任何惯性系中都有相同的速率。 这个解释其实和我们的日常生活是有尖锐矛盾的,下面我们通过例子来详细体会一下这种矛盾到底尖锐到 什么程度。 我们设想一个场景:A 和 B 两个人,A 静止在地面上,A 用一把枪瞄准了 B,在某时刻开了一枪,B 在子 弹出膛的瞬间以一个恒定的速度逃跑。我们知道,如果 B 逃跑的速度非常快,要是和子弹速度一样的话, 子弹是追不上 B 的,看下图
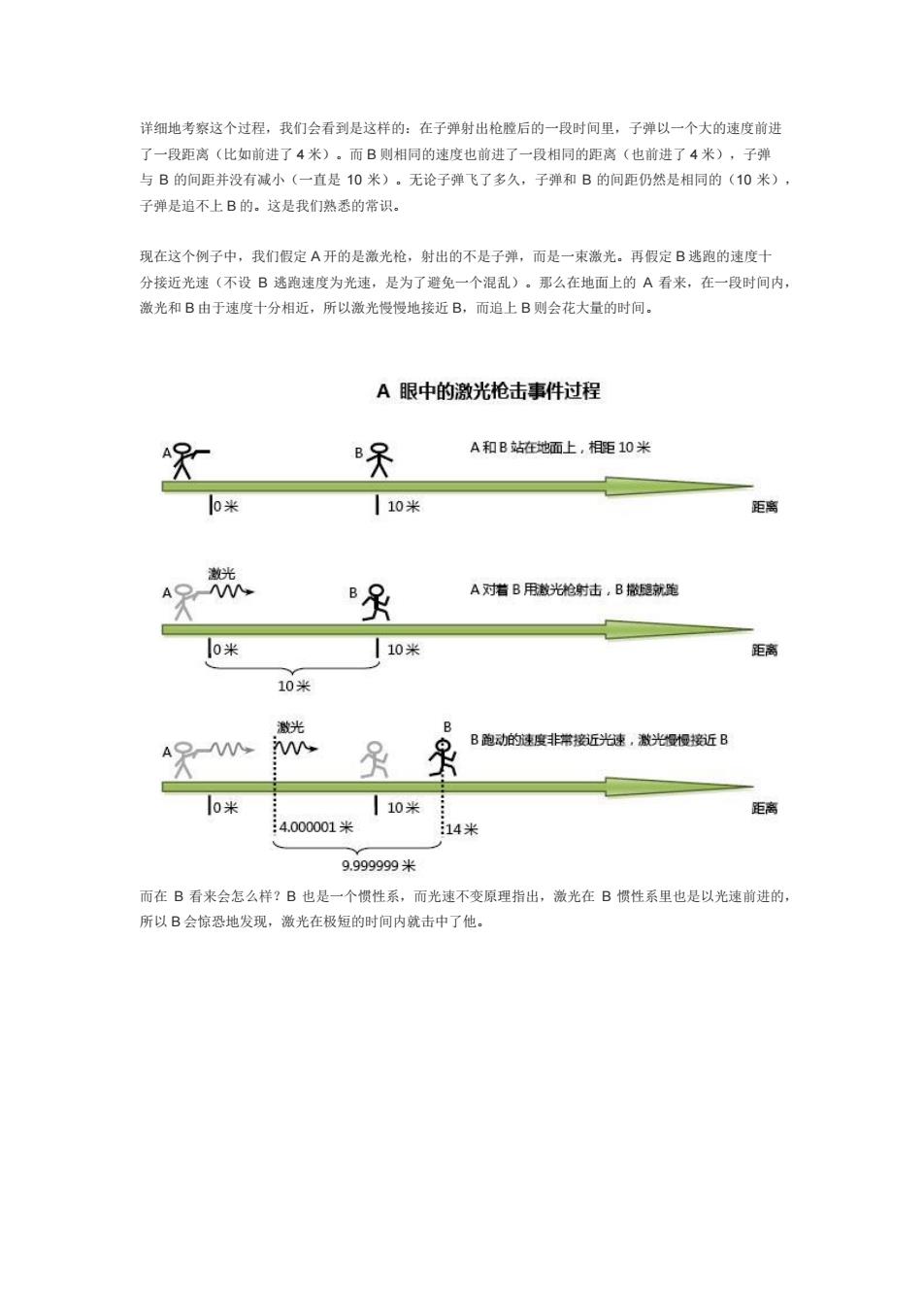
详细地考察这个过程,我们会看到是这样的:在子弹射出枪膛后的一段时间里,子弹以一个大的速度前进 了一段距离(比如前进了4米)。而B则相同的速度也前进了一段相同的距离(也前进了4米),子弹 与B的间距并没有减小(一直是10米)。无论子弹飞了多久,子弹和B的间距仍然是相同的(10米), 子弹是追不上B的。这是我们熟悉的常识。 现在这个例子中,我们假定A开的是激光枪,射出的不是子弹,而是一束激光。再假定B逃跑的速度十 分接近光速(不设B逃跑速度为光速,是为了避免一个混乱)。那么在地面上的A看来,在一段时间内, 激光和B由于速度十分相近,所以激光慢慢地接近B,而追上B则会花大量的时间。 A眼中的激光枪击事件过程 A和B贴在地面上,相距10米 lb米 |10米 距离 激光 A, A对着B用数光枪射击,B就跑 0米 |10米 距离 10米 激光 M B跑动的速度非常接资近光速,激光慢慢接宽近B 0米 |10米 距离 4.000001米 14米 9.999999米 而在B看来会怎么样?B也是一个惯性系,而光速不变原理指出,激光在B惯性系里也是以光速前进的, 所以B会惊恐地发现,激光在极短的时间内就击中了他
详细地考察这个过程,我们会看到是这样的:在子弹射出枪膛后的一段时间里,子弹以一个大的速度前进 了一段距离(比如前进了 4 米)。而 B 则相同的速度也前进了一段相同的距离(也前进了 4 米),子弹 与 B 的间距并没有减小(一直是 10 米)。无论子弹飞了多久,子弹和 B 的间距仍然是相同的(10 米), 子弹是追不上 B 的。这是我们熟悉的常识。 现在这个例子中,我们假定 A 开的是激光枪,射出的不是子弹,而是一束激光。再假定 B 逃跑的速度十 分接近光速(不设 B 逃跑速度为光速,是为了避免一个混乱)。那么在地面上的 A 看来,在一段时间内, 激光和 B 由于速度十分相近,所以激光慢慢地接近 B,而追上 B 则会花大量的时间。 而在 B 看来会怎么样?B 也是一个惯性系,而光速不变原理指出,激光在 B 惯性系里也是以光速前进的, 所以 B 会惊恐地发现,激光在极短的时间内就击中了他

B眼中的激光枪击事件过程 光 B看见位于-10米的A向自己射出激光 -10米 0米 距离 10米 激光 B 星然B发现A离开自己的速度非常接近光速,但是A射出的激光还 是以光速接近自己,在极短的时间内,激光就射中了自己 -10.000001米 0米 距离 如果仔细对比A和B这两人对同一个过程(A向B射击激光束,最后B被激光束击中)的观察,会发现 俩人的看法具有很大的差异,在这里的巨大差异体现在两人对激光自射出枪膛到击中B所用的时间是完全 不同的:A发现激光束击中B发生在激光束被射出后的很长的一段时间后(比如1小时之后),而B却 发现激光束自被射出到射中自己,花了连1微妙都不到的时间。这是多么不可思议的事情?对于同一个过 程,两个处在不同运动状态的观察者,居然会有截然不同的描述。 我们现在把这个例子中的AB初始间距拉得长一点,比如300万公里。于是在B的眼里,自激光发射到击 中B的过程中,B竞然还享受了人生最后的一根烟。他抽这根烟,花了10秒钟。那么A怎么看呢?很明 显,A发现激光击中B,和B抽完那根烟是同时同地发生的事情。而A发现激光束追到B花了1个小时 的时间,那也就是说,A发现B的这根烟,抽了1个小时。A发现B抽烟的速度很慢,不但如此,A还发 现B做任何事情的速度都很慢,比如点烟、心跳、呼吸等,都极其缓慢。同样,A也发现B手上的手表 指针也走得很慢很慢。这是什么?这就是“时间膨胀”:A发现B惯性系中的时间,走得比A自己要慢。 这在我们日常经验中是不可思议的,然而光速不变原理指出,事情就是这样的。 现在的情况是这样的:我们假设光速不变是正确的,而这个假设成立,则意味着传统的关于空间距离和时 间间隔的关系(两者独立无关)再也不能成立了,否则就会出现上述这种百思不得其解的结果。那么也就 是说,假设光速不变成立,那么我们就必须寻找一种新的空间距离和时间间隔之间的关系,使得在这种新 的关系下,光速不变成立。 原有的空间距离和时间间隔的关系就是牛顿力学中的那一套:同一个空间距离在不同的观察者眼里都是相 同的:同一个时间间隔在不同观察者眼里也是相同的。也就是说,任何空间距离和时间间隔都是不变量, 与观察者的位置、时间和运动速度都无关。 很显然,按照这套我们熟知的关系,对上面这个例子是完全无法解释的,也就是说,牛顿的那套时空关系, 与光速不变假设是你死我活地彻底对立的。 爱因斯坦在他的一篇论文《相对性原理及其结论》中有这么一句话:“现在我们假设,在坐标系没有加速 的前提下,这些钟可以这样来校准,使得真空中任何光线的传播速度一用这些钟来量度一总是等于一个 普适常数c
如果仔细对比 A 和 B 这两人对同一个过程(A 向 B 射击激光束,最后 B 被激光束击中)的观察,会发现 俩人的看法具有很大的差异,在这里的巨大差异体现在两人对激光自射出枪膛到击中 B 所用的时间是完全 不同的:A 发现激光束击中 B 发生在激光束被射出后的很长的一段时间后(比如 1 小时之后),而 B 却 发现激光束自被射出到射中自己,花了连 1 微妙都不到的时间。这是多么不可思议的事情?对于同一个过 程,两个处在不同运动状态的观察者,居然会有截然不同的描述。 我们现在把这个例子中的 AB 初始间距拉得长一点,比如 300 万公里。于是在 B 的眼里,自激光发射到击 中 B 的过程中,B 竟然还享受了人生最后的一根烟。他抽这根烟,花了 10 秒钟。那么 A 怎么看呢?很明 显,A 发现激光击中 B,和 B 抽完那根烟是同时同地发生的事情。而 A 发现激光束追到 B 花了 1 个小时 的时间,那也就是说,A 发现 B 的这根烟,抽了 1 个小时。A 发现 B 抽烟的速度很慢,不但如此,A 还发 现 B 做任何事情的速度都很慢,比如点烟、心跳、呼吸等,都极其缓慢。同样,A 也发现 B 手上的手表 指针也走得很慢很慢。这是什么?这就是“时间膨胀”:A 发现 B 惯性系中的时间,走得比 A 自己要慢。 这在我们日常经验中是不可思议的,然而光速不变原理指出,事情就是这样的。 现在的情况是这样的:我们假设光速不变是正确的,而这个假设成立,则意味着传统的关于空间距离和时 间间隔的关系(两者独立无关)再也不能成立了,否则就会出现上述这种百思不得其解的结果。那么也就 是说,假设光速不变成立,那么我们就必须寻找一种新的空间距离和时间间隔之间的关系,使得在这种新 的关系下,光速不变成立。 原有的空间距离和时间间隔的关系就是牛顿力学中的那一套:同一个空间距离在不同的观察者眼里都是相 同的;同一个时间间隔在不同观察者眼里也是相同的。也就是说,任何空间距离和时间间隔都是不变量, 与观察者的位置、时间和运动速度都无关。 很显然,按照这套我们熟知的关系,对上面这个例子是完全无法解释的,也就是说,牛顿的那套时空关系, 与光速不变假设是你死我活地彻底对立的。 爱因斯坦在他的一篇论文《相对性原理及其结论》中有这么一句话:“现在我们假设,在坐标系没有加速 的前提下,这些钟可以这样来校准,使得真空中任何光线的传播速度 -- 用这些钟来量度 -- 总是等于一个 普适常数 c

这句话是在100年前说的,其中的一些用词与现在的用词有一些差异。这里我尝试下用现在的用词重复一 遍:“现在我们假设,在参考系没有加速的前提下,这些钟可以这样来校准,使得真空中任何光束的传播 速度一用这些钟来测量一总是等于一个恒定的常数c”。在这里,没有被加速的参考系就是惯性系。 而句中的“钟”十分耐人寻味,在这里其实就代表了“对时间的测量”。 这句话的意思就是:原有的校准钟的方式是无效的,因为用按照原有的校准方式的钟,我们无法让光束在 任何惯性系中的传播速度保持一个恒定的常数。我们要寻找一种新的校准方式,也就是新的空间距离和时 间间隔的关系。 而在新的关系下,上面这个例子应该是十分标准的一种现象了:在一个观察者眼里具有极其漫长的过程, 而在另一个观察者眼里却是一瞬间完成。从这里可以看出,时间在不同观察者中不再有统一的测量了,不 同观察者可以有不同的时间。 现在的问题就成为了一个“解答题":已知存在一种时空关系,可以使得上述这个按照寻常思维会感到匪夷 所思的光速不变例子合理地成立,求这个时空关系。 答案很明显,新的时空关系就是洛伦兹变换方程组。 我们接着看下面这个例子: 在一个地面上竖着放着一个手电筒,地面上方有一个水平放置的镜子。在某一时刻打开手电筒,光束从手 电筒出发,到达镜子后反射,最后回到手电筒。整个过程中,光束的运动轨迹位于同一直线上。这个过程 很清晰,但我们要指出的是,这是一个站在地面上与手电筒相对静止的观察者的观察结果。 如果有一个以一定速度向左边运动的观察者,他会发现什么呢? 他会发现,地面、手电筒和镜子全部以一个速度向右边运动,手电筒发射出去的光线也同样有一个向右边 的运动分量。最终这束光线的运动轨迹为一个三角形,如下图①②③④
这句话是在 100 年前说的,其中的一些用词与现在的用词有一些差异。这里我尝试下用现在的用词重复一 遍:“现在我们假设,在参考系没有加速的前提下,这些钟可以这样来校准,使得真空中任何光束的传播 速度 —— 用这些钟来测量 —— 总是等于一个恒定的常数 c”。在这里,没有被加速的参考系就是惯性系。 而句中的“钟”十分耐人寻味,在这里其实就代表了“对时间的测量”。 这句话的意思就是:原有的校准钟的方式是无效的,因为用按照原有的校准方式的钟,我们无法让光束在 任何惯性系中的传播速度保持一个恒定的常数。我们要寻找一种新的校准方式,也就是新的空间距离和时 间间隔的关系。 而在新的关系下,上面这个例子应该是十分标准的一种现象了:在一个观察者眼里具有极其漫长的过程, 而在另一个观察者眼里却是一瞬间完成。从这里可以看出,时间在不同观察者中不再有统一的测量了,不 同观察者可以有不同的时间。 现在的问题就成为了一个“解答题”:已知存在一种时空关系,可以使得上述这个按照寻常思维会感到匪夷 所思的光速不变例子合理地成立,求这个时空关系。 答案很明显,新的时空关系就是洛伦兹变换方程组。 我们接着看下面这个例子: 在一个地面上竖着放着一个手电筒,地面上方有一个水平放置的镜子。在某一时刻打开手电筒,光束从手 电筒出发,到达镜子后反射,最后回到手电筒。整个过程中,光束的运动轨迹位于同一直线上。这个过程 很清晰,但我们要指出的是,这是一个站在地面上与手电筒相对静止的观察者的观察结果。 如果有一个以一定速度向左边运动的观察者,他会发现什么呢? 他会发现,地面、手电筒和镜子全部以一个速度向右边运动,手电筒发射出去的光线也同样有一个向右边 的运动分量。最终这束光线的运动轨迹为一个三角形,如下图①②③④

T ① 9e 77777777777777777777777 ③ ④ 1111117771117 ①200 仔细观察①②③④这个过程,会很有意思的。在这里要运用光速不变原理,也就是说,在一个运动观察者 眼里,走三角形长边轨迹的光束,其速度还是光速。想一想,在地面静止观察者眼里,垂直上下的光线速 度是光速C:在运动观察者眼里,多了一个水平分量后的光的“合速度”,还是光速℃,而垂直方面的速度, 显然比光速c要小一些!产生这个奇怪现象的原因是什么?就是“时间膨胀”:向左运动的观察者发现,地 面惯性系的时间走得慢了,光线在垂直方面的速度也变慢了。可是光线的整体速度,由于还存在一个水平 速度,还是保持着原来的光速c。 现在来定量地看看,这其中的一系列因素之间的关系是什么。在这里设A系中光线从手电筒到达镜子经过 了△t时间,在B系中光线从手电筒到达镜子经过了△F时间
仔细观察①②③④这个过程,会很有意思的。在这里要运用光速不变原理,也就是说,在一个运动观察者 眼里,走三角形长边轨迹的光束,其速度还是光速。想一想,在地面静止观察者眼里,垂直上下的光线速 度是光速 c;在运动观察者眼里,多了一个水平分量后的光的“合速度”,还是光速 c,而垂直方面的速度, 显然比光速 c 要小一些!产生这个奇怪现象的原因是什么?就是“时间膨胀”:向左运动的观察者发现,地 面惯性系的时间走得慢了,光线在垂直方面的速度也变慢了。可是光线的整体速度,由于还存在一个水平 速度,还是保持着原来的光速 c。 现在来定量地看看,这其中的一系列因素之间的关系是什么。在这里设 A 系中光线从手电筒到达镜子经过 了 Δt 时间,在 B 系中光线从手电筒到达镜子经过了 Δt’ 时间