
一、 选择题(10小题,每小题3分,共30分) 1、一电动小车从静止开始在光滑的直线轨道上行驶。若小车的电动机的功率恒定, 那么它所走的路程3与时间t的关系如何() A、Sct B、Sct2 c、s2ct D、s2cf3 2、一质点沿半径为R的圆周按规律5=加-c?运动,其中b、c是正的紫量。在 切向加速度与法向加速度的大小相等时,质点运动速度的大小为( ) A、V2CR B、VCR c、 b2 bR b2 bR d2Vc D、 一十 c 2Vc 3、在S制中,一些物理量的量纲如不,其中冲量的量纲为( A、MLT-l B、MLT2 C、ML2T-J D、ML2T-2 4、一力学系统由两个质点组成,它们之间只有引力作用。若两质点所受外力的矢量 和为零,由此可知系统( )。 A、:动量和机械能都守恒 B、动量和机械能都不守恒 C、 动量守恒,但机械能是否守恒不能断定 D、 机械能守恒,但动量是否守恒不能断定 5、地球的质量为m,太阳的质量为M,地心对太阳中心的距离为R,引力常数为G, 地球绕太阳转动的轨道角动量大小为( A、mGMR B、√GMm/R C、MmVG/RD、√GMm/2R 6、如图所示,在水平光滑的圆盘上,有一质量为m的质点,拴在一根穿过圆盘中心 光滑小孔的轻绳上。开始时质点离中心的距离为”,并以角速度⊙转动。今以均匀 速度向下拉绳,将质点拉至离中心r/2处时,拉力所作的功为( A、 1 B、 C、 F > D、 r202 2

7、倔强系数分别为k和k,的两根弹簧,按图所示的三种方式与物体组成振动系统。 如果不计摩擦,那么它们的周期的关系应是( ) A、T=T3≠T B、T=T≠T C、T=T3=T D、T≠T2≠T 振动系统1 振动系统2 振动系统3 8、由图所给的波形图和P处质元振动图,可得该简谐波方程为( C、y=0.02cos 2 D、条件不足不能确定 y(m) y(m) 0.02 0 x(m) 0 0.2 t(s) (a)-0时波形图 (b)P处质元振动图 9、如图所示,S,,为两平面波波源,它们的振动方程分别为y=0.3c0s(2+)cm, 和y2=0.4c0s(2πt+π)cm,它们发出的波在P点 相遇而迭加,图中r=40cm,72=45cm.如图两波 波速都为v=20cm·s,那么两波在P点叠加后的 合振幅为( A、0.1cmB、0.5cm C、0.7cmtD、以上情况都不是 S2 10、关于功和能量的概念,以下说法中正确的是( A、保守力作正功,系统内相应的势能增加 B、作用力和反作用力大小相等方向相反,所以二者作功的代数和必为零 C、质点运动经一闭合路径回到初始点,则保守力对质点作的功为零 D、质点运动经一闭合路径回到初始点,则系统的机械能守恒 应存海滑(产

,淡数味两”过式做会驱杀君型, 二、填空题(10小题,每小题3分,共30分)别 表醉破不果测 1、质量为m的物体,在力F=-0mx作用下沿x轴运动,其中0为正的常系数。 己知在t=0时,质点在x。=A处,且速度。=0,则此物体的运动速度的表达式为 V= ,物体的运动方程为x= 2、一质量为M的质点沿x轴正向运动,假设该质点通过坐标为x时的速度大小为 心(k为正常量),则此时作用于该质点上的力F= ,该质点从 x=x,点出发运动到x=x,处所经历的时间△1= 3、如图所示,质量为m的质点,在竖直平面内作半径为r、速率为v的匀速圆周运 动,在由点A运动到点B的过程中,所受合外力的冲量为= ;除重力以 外,其它外力对物体所做的功为W= B 《这位清在是两女满心,,4置 +元拉1=r明 4、已知质点在F=2i+3j处受到外力F=ti+t2(SI),求第2秒末的该力相对于 。 原点的力矩M= 5、如图所示,一根长I,质量为m的匀质细棒可绕通过点0的水平光滑轴在竖直平 面内转动,则棒的转动惯量I= 品;当棒由水平位置静止释放转 动到图示的位置时,则其角速度0= 1/3 7的生行你卧达 6、一长为1,质量均匀的链条,放在光滑的水平桌面上,若使其长度的/2悬于桌 边下,然后由静止释放,任其滑动,则链条全部离开桌面时的速率为
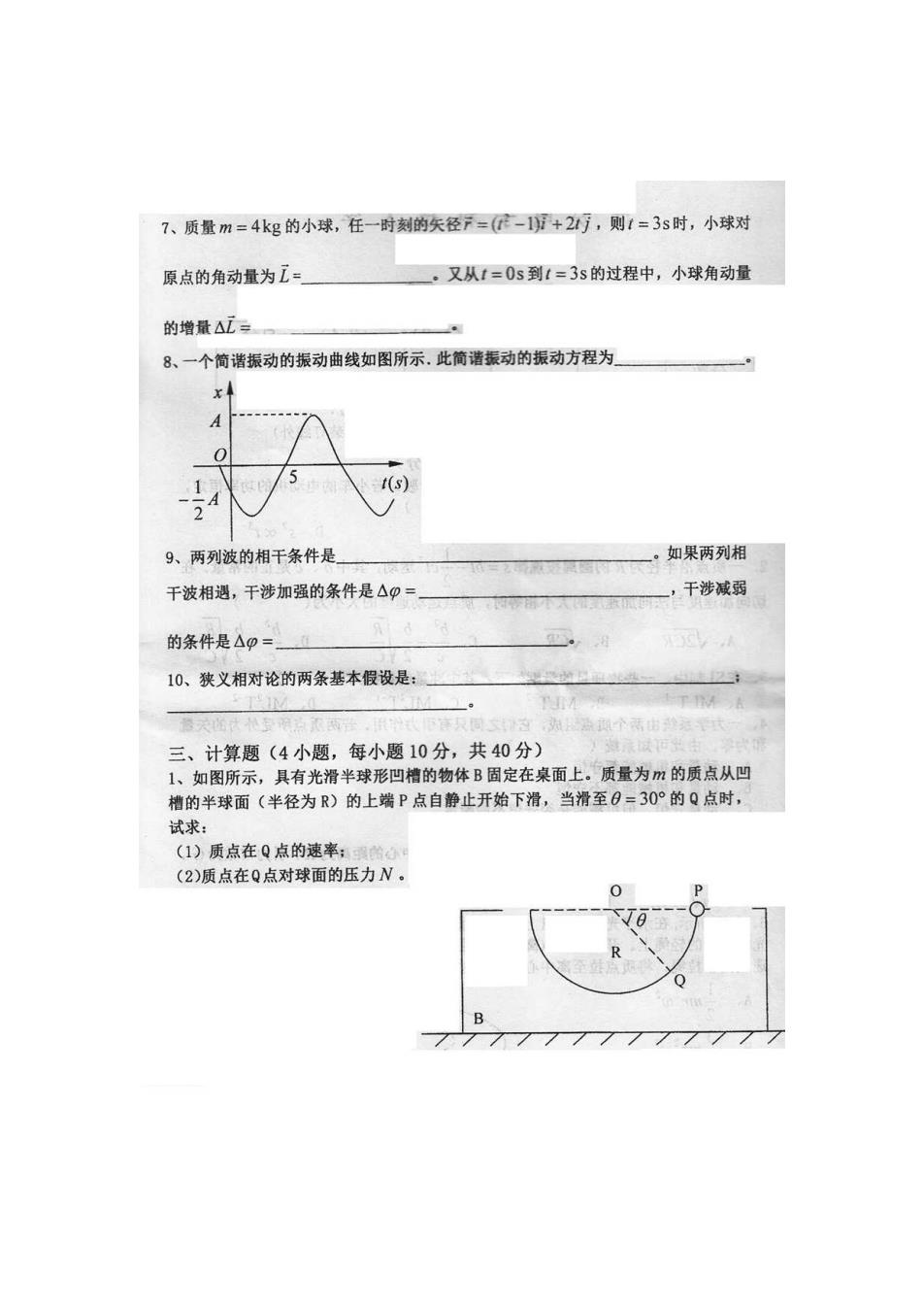
7、质量m=4kg的小球,任一时刻的矢径F=-1)+21万,则1=3s时,小球对 原点的角动量为= 又从1=0s到t=3s的过程中,小球角动量 的增量△L= 8、一个简谐振动的振动曲线如图所示.此简谐振动的振动方程为 9、两列波的相干条件是 如果两列相 干波相遇,干涉加强的条件是△0= 干涉减弱 的条件是△p= 。 10、狭义相对论的两条基本假设是: 山2; T1 三、计算题(4小题,每小题10分,共40分) 1、如图所示,具有光滑半球形凹槽的物体B固定在桌面上。质量为m的质点从凹 槽的半球面(半径为R)的上端P点自静止开始下滑,当滑至O=30°的Q点时, 试求: (1)质点在Q点的速率:喻 (2)质点在Q点对球面的压力N。 0 R
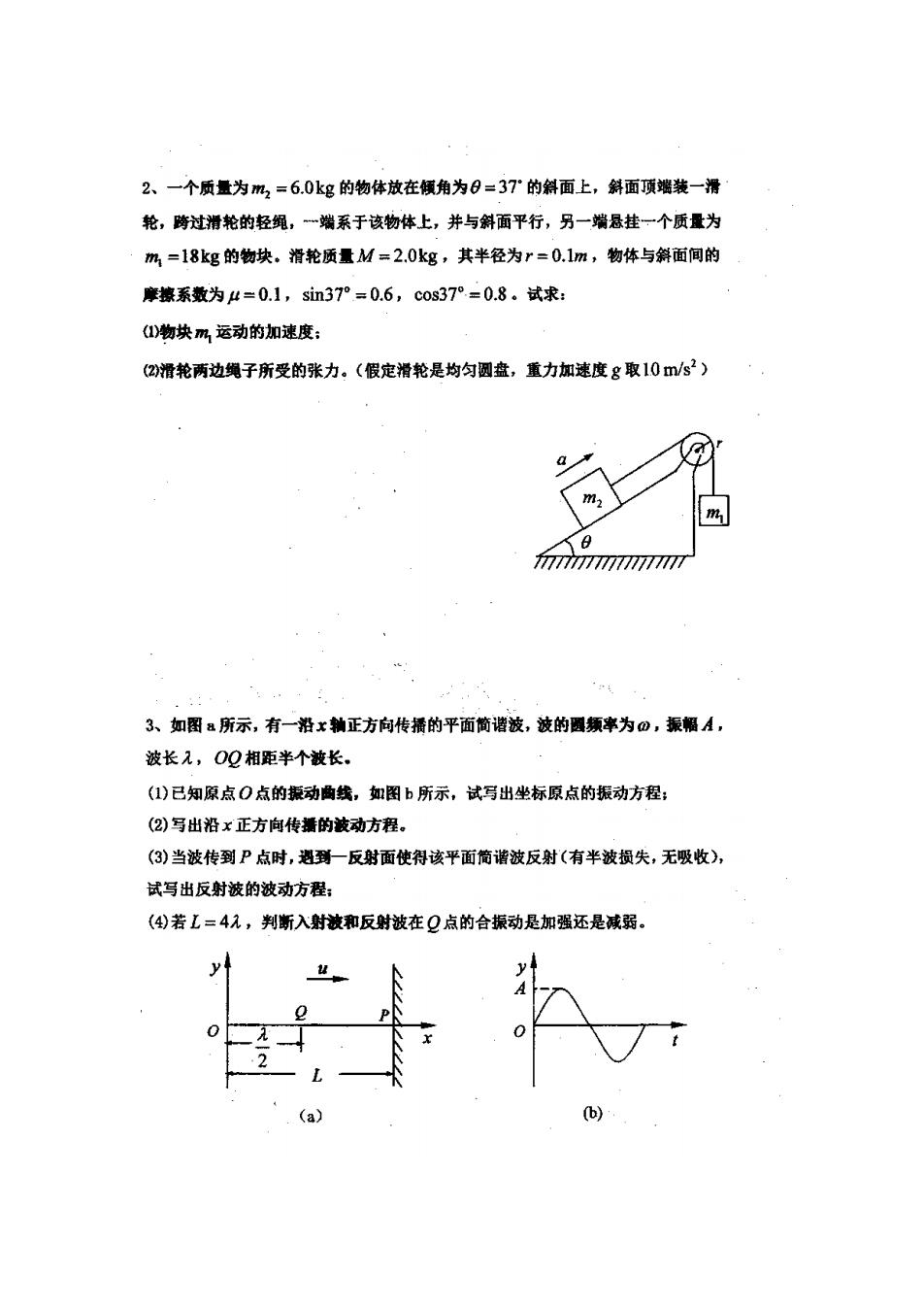
2、一个质量为m2=6.0kg的物体放在倾角为日=37”的斜面上,斜面项端装一滑 轮,跨过滑轮的轻绳,一端系于该物体上,并与斜面平行,另一端悬挂一个质量为 m1=18kg的物块。滑轮质量M=2.0kg,其半径为r=0.1m,物体与斜面间的 摩擦系数为4=0.1,sin37°=0.6,cos37°=0.8。试求: 1)物块m运动的加速度: (2滑轮两边绳子所受的张力。(假定滑轮是均匀圆盘,重力加速度g取10/s2) a m, imm7mn77m 3、如图a所示,有一沿x轴正方向传播的平面简谐波,波的圆频率为0,振幅A, 波长入,O2相距半个被长. (1)已知原点O点的振动胸线,如图b所示,试写出坐标原点的振动方程: (2)写出沿x正方向传播的波动方程。 (3)当波传到P点时,遇到一反射面使得该平面简谐波反射(有半波损失,无吸收), 试写出反射波的波动方程: (4)若L=4入,判断入射波和反射波在Q点的合振动是加强还是减弱。 (b)