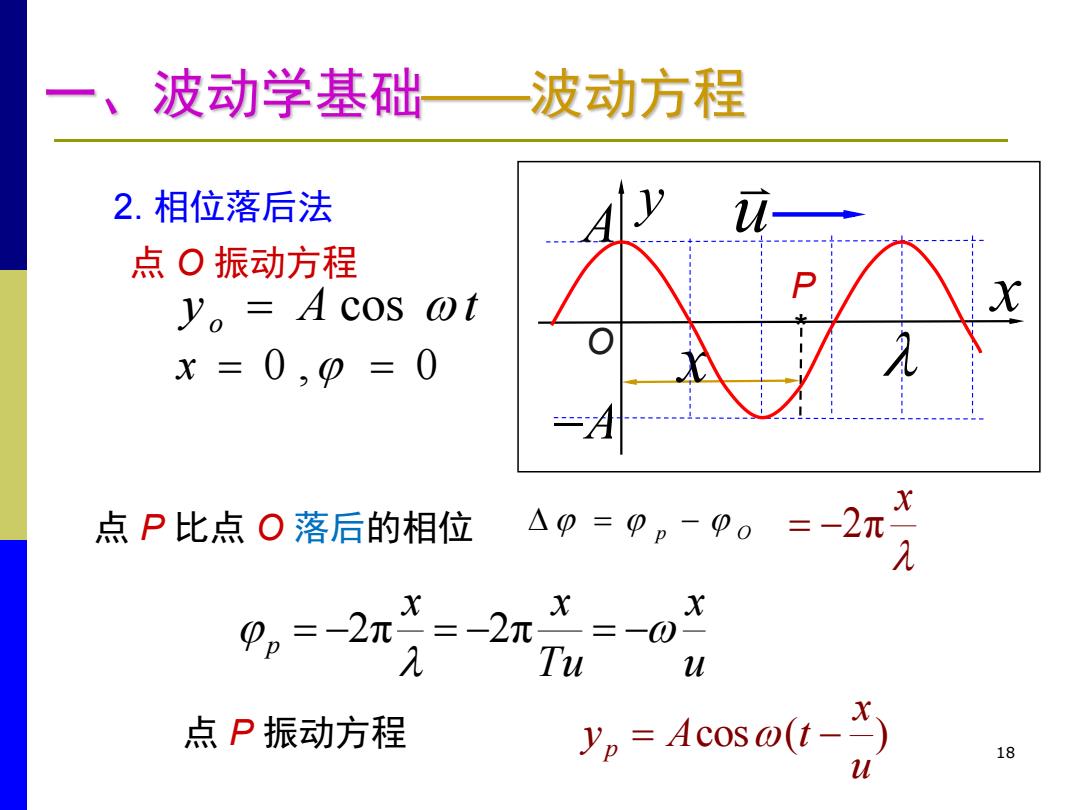
波动学基础 —波动方程 2.相位落后法 y⑦ 点O振动方程 y。=Ac0S s wt x=0,0=0 X 点P比点O落后的相位 A0=0p-00=-2T X X X 0p=-2π =-2元 =一0 Tu U 点P振动方程 Yy=Acos@(t-) 18 u
18 点 P 比点 O 落后的相位 p - O x -2π u x Tu x x p -2π -2π - cos ( ) u x y A t 点 P 振动方程 p - y A t o cos 点 O 振动方程 x 0 , 0 P x * y x u A -A O 2. 相位落后法
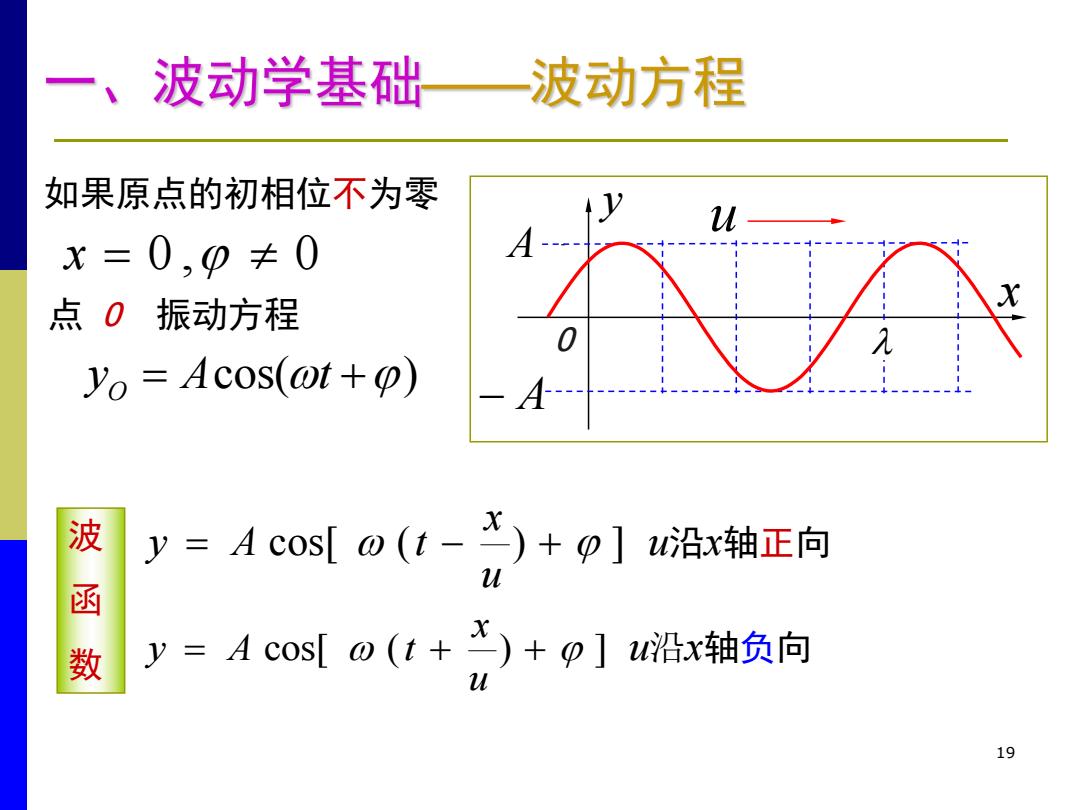
、波动学基础一 波动方程 如果原点的初相位不为零 u x=0,0≠0 点0振动方程 Yo Acos(@t+p) 波 y=Acos[@(i-)+9] u沿x轴正向 函 数 y=Acosl w(t+)+p]u沿x轴负向 19
19 y Acos(t ) O 点 O 振动方程 cos[ ( ) ] u x y A t u沿x轴负向 波 函 数 cos[ ( - ) ] u沿x轴正向 u x y A t y x u A - A O x 0 , 0 如果原点的初相位不为零

一、波动学基础一 波动方程 >质点的振动速度,加速度 =-@dsinlo(t-+pl 8t 0y-w2 deo®1-为+0 0t2 W 20
20 Ø质点的振动速度,加速度 - sin[( - ) ] u x A t t y v cos[ ( ) ] 2 2 2 - - u x A t t y a

一、波动学基础一 波动方程 cosfcos2 u 波函数的物理意义: 1、当x固定时,波函数表示该点的简谐运动方程,并给出 该点与点O振动的相位差 A0=-0x=-2 X 元 l y(x,t)=y(x,t+T) (波具有时间的周期性)
21 波函数的物理意义: cos[ ( ) ] cos[2 π( ) ] - - x T t A u x y A t 1、当 x 固定时,波函数表示该点的简谐运动方程,并给出 该点与点 O 振动的相位差. λ x u x - -2 π (波具有时间的周期性) y(x,t) y(x,t T) P x * y x u A -A O

波动学基础一 波动方程 y=Acoslo(cosl2 u 波函数的物理意义: 2、当一定时,波函数表示该时刻波线上各点相对其平衡 位置的位移,即此刻的波形 y(x,t)=y(x+人,t)(波具有空间的周期性) 22
22 y(x,t) y(x ,t)(波具有空间的周期性) 2、当 一定时,波函数表示该时刻波线上各点相对其平衡 位置的位移,即此刻的波形. t 波函数的物理意义: cos[ ( ) ] cos[2 π( ) ] - - x T t A u x y A t