
第8卷第1期 智能系统学报 Vol.8 No.1 2013年2月 CAAI Transactions on Intelligent Systems Feh.2013 D0I:10.3969/j.issn.1673-4785.201208032 网络出版地址:http://ww.cnki.net/kems/detail/23.1538.TP.20130125.1518.009.html 一种基于改进Theta*的机器人路径规划算法 肖国宝,严宣辉 (福建师范大学数学与计算机科学学院,福建福州350007) 摘要:对Theta'算法进行改进,并用于解决机器人路径规划问题.首先,将障碍物对机器人产生的斥力作为一种惩 罚函数加入到启发函数中,并合理地选择惩罚函数权重以确定启发函数.在此基础上,改进A·算法的变种一Te a·算法,提出对路径进行平滑处理的PS_Theta·算法.最后在二维仿真环境中进行验证及数据统计,并推广至三维 复杂环境中,实验结果证明了算法的合理性与有效性. 关键词:机器人;路径规划;启发函数;A'算法;Theta"算法;PS_Theta·算法 中图分类号:TP242.6文献标志码:A文章编号:16734785(2013)01005808 A path planning algorithm based on improved Theta*for mobile robot XIAO Guobao,YAN Xuanhui (School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China) Abstract:Current research indicates the Theta'algorithm has improved in terms of solving the path planning for a mobile robot.First,the repulsion,which is generated by the obstacles to the robot,has been added to the heuristic function as a penalty function.Based on reasonably choosing the weight of the penalty function,the heuristic func- tion was also identified.Due to this,the Theta*algorithm,a variant of A*algorithm,was improved,thereby crea- ting a smooth route for the PS_Theta'algorithm.In the end,a test was conducted and analyzed,not only in the 2-D coordination simulated environment but also in the 3-D complex environment,and the data validated the algo- rithm reasonably and effectively. Keywords:mobile robot;path planning;heuristic function;A'algorithm;Theta'algorithm;PS_Theta'algorithm 路径规划是智能交通、智能网络、机器人等人工 的问题.目前,确定性环境的导航控制方法已取得了 智能研究领域的重要分支,所谓移动机器人路径规 大量的研究和应用成果56,在二维未知环境中的 划技术,就是机器人根据自身传感器对环境的感知, 导航控制方面已展开了一些研究,并提出了若干方 在线规划出一条安全、可靠的运行路径,同时高效完 法?9);但随着人类活动空间的扩张,已有的二维路 成作业任务2].它是一个比较复杂的带约束条件 径规划技术越来越满足不了许多领域的需求,人们 的优化问题,约束条件包括但不限于:不与障碍物碰 迫切需要一套成熟可靠的三维空间路径规划技 撞、运动路径最短、尽量远离障碍物、路径尽量平滑 术1 等34 机器人路径规划需要考虑很多因素,其中主要 未知环境下的机器人路径规划是智能体实现其 包括环境的不确定性和动态特性、规划算法的优越 在线规划的前提,也是移动机器人导航中一个重要 性、实时能力等.三维环境下的机器人路径规划问题 由于运动学和动力学约束变得非常复杂,机器人的 收稿日期:201208-24.网络出版日期:201301-25 基金项目:国家自然科学基金资助项目(61175123);福建省省属高校 自由度也大幅度增加,这要求规划算法的实时性要 科研专项重点项目(K2009006);福建省高校服务海西建 比较好,防止出现数据爆炸的情况.针对盲目搜索的 设重点项目. 通信作者:严宣辉.E-mail:x-gh@163.com. 效率较低,会耗费过多的计算空间与时间,目前用于

第1期 肖国宝,等:一种基于改进Theta'的机器人路径规划算法 ·59. 三维路径规划比较常见的算法有A·[8]、Diskstra、 D·-lite、贪婪搜索、四/八叉树搜索9以及这些算法 的改进「1o1.采用的搜索策略如宽度优先、深度优 5 先、启发式、非启发式搜索等 经典的启发式搜索算法一A·算法是由P.E. Hart等在20世纪60年代提出的,该算法在各个领 域得到了广泛的应用[2].A·算法也是目前用来解 决游戏地图路径搜索问题最优的算法,但该算法只 图1城市环境模型 能用在格子环境中,这在一定程度上限制了其进一 Fig.1 Urban environment model 步的推广.Alex等在2007年提出了一种A*算法的 20 变种一Theta'算法31,突破了格子的限制,允许 16 》」 以任意角度改变路径的方向. 12 绿汤 启发函数是评定候选扩展节点的方法,以便确 定哪个节点最有可能在通向目标的最佳路径上,它 ® 将会影响到整个算法的性能和效果.在大部分启发 16 粉 式搜索算法中的启发函数只估算到起始点和目标点 八®12160 的代价,没有合理地利用障碍物信息,这会限制其用 图2普通环境模型 于解决机器人路径规划问题时的进一步推广。 Fig.2 Common environment model 本文将局部环境的障碍物对机器人产生的斥力 任意时刻,在二维地图中,机器人的运动方向有 作为惩罚函数引入到启发函数中,为机器人提供了 8个,如图3所示,机器人可以到达相邻栅格的各个 更加可靠的启发信息.首先,利用仿真实验的数据统 顶点;在三维地图中,机器人的运动方向有26个,如 计合理地选择惩罚函数权重,以确定启发函数;然后 图4所示,机器人可以到达相邻立方格的各个顶点 在此启发策略的基础上,改进A·算法的变种 Theta·算法,用PS_Theta·算法对路径进行平滑处 理,优化路径. 1算法描述 1.1三维环境模型 移动机器人环境模型问题就是机器人根据传感 图3二维运动方向 器的感知获得环境的二维或三维空间模型.单元分 Fig.3 The direction of movement in 2-D environment 解建模是典型的环境模型,其主要思想是将环境离 散化为若干个规则的相同大小的基本单元一三维 的立方格,通过二值信息便可以对障碍物和自由空 间进行标识,因此使用简单的传感器即可获得创建 地图的信息.然而,立方格的大小直接影响着移动机 器人环境信息存储量的大小和规划时间的长短,立 方格选得小,环境分辨率高,但环境信息存储量大, 图4三维运动方向 相应的干扰信号相对增加,使得决策工作量加大,最 Fig.4 The direction of movement in 3-D environment 终导致规划速度变慢,降低系统的实时性;当立方格 机器人路径规划问题就是在图中寻找一个从起 变大时,虽然抗干扰能力增强,但环境分辨率下 始点S到目标点T之间点的集合,并要求相邻点之 降,在密集障碍物环境中不利于规划出有效的路 间的线段连接没有经过障碍物, 径4 1.2改进启发函数 在Matlab7.6中建立2种常见的模型:1)城市环 在启发式搜索算法中,引入当前节点x的启发 境模型,如图1;2)普通环境模型,如图2.其中,将机器 式估价函数f(x),其函数的定义式为 人看作质点,不能碰到环境中的任何障碍物. f(x)=a×g(x)+B×h'(x). (1)
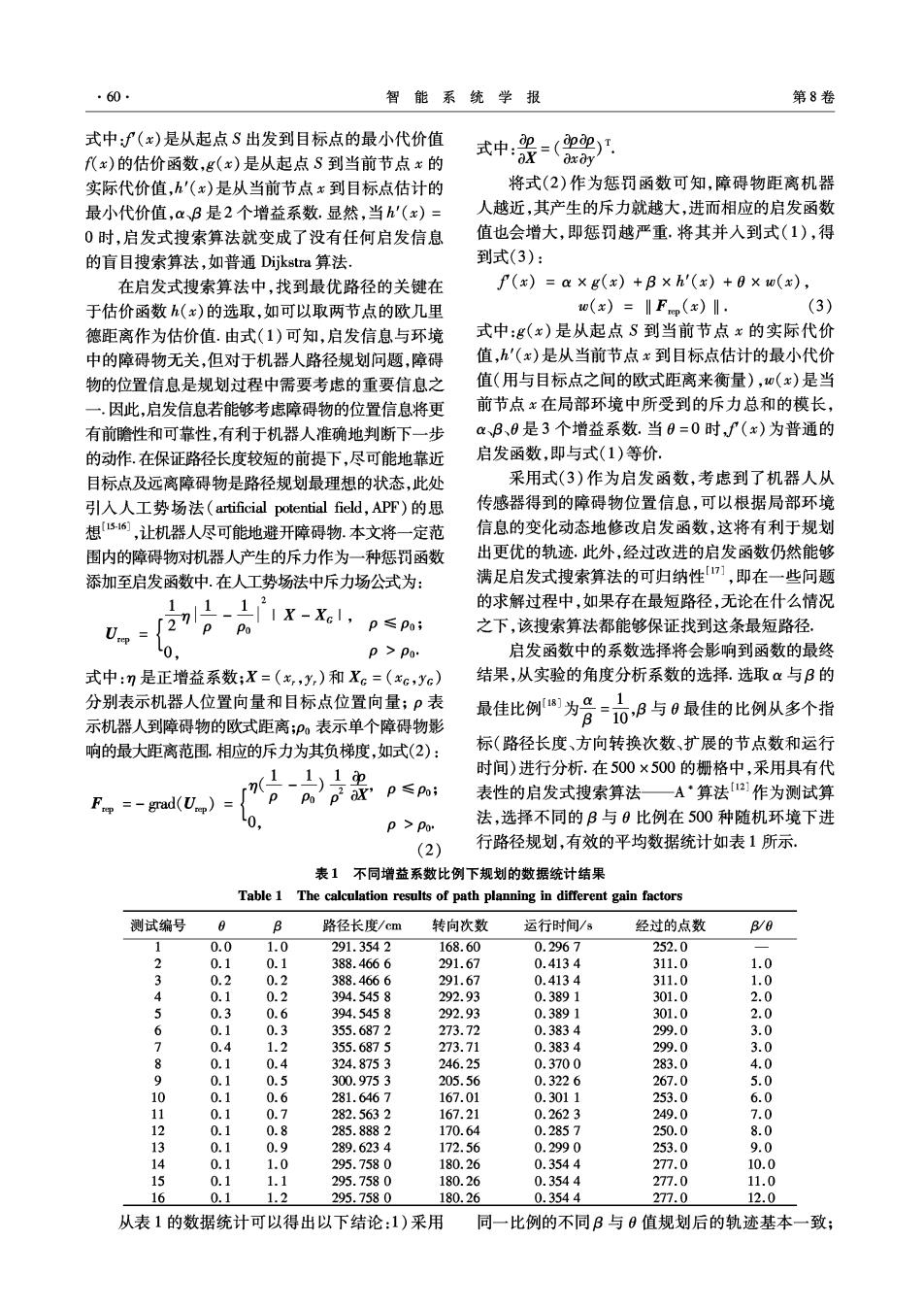
·60 智能系统学报 第8卷 式中:f(x)是从起点S出发到目标点的最小代价值 式中:2=(22) f代x)的估价函数,g(x)是从起点S到当前节点x的 aX-、x0y 实际代价值,h'(x)是从当前节点x到目标点估计的 将式(2)作为惩罚函数可知,障碍物距离机器 最小代价值,αB是2个增益系数.显然,当h'(x)= 人越近,其产生的斥力就越大,进而相应的启发函数 0时,启发式搜索算法就变成了没有任何启发信息 值也会增大,即惩罚越严重.将其并入到式(1),得 的盲目搜索算法,如普通Dijkstra算法. 到式(3): 在启发式搜索算法中,找到最优路径的关键在 f(x)=a×g(x)+B×h'(x)+0×w(x), 于估价函数h(x)的选取,如可以取两节点的欧几里 0(x)=‖Fp(x)‖. (3) 德距离作为估价值.由式(1)可知,启发信息与环境 式中:g(x)是从起点S到当前节点x的实际代价 中的障碍物无关,但对于机器人路径规划问题,障碍 值,'(x)是从当前节点x到目标点估计的最小代价 物的位置信息是规划过程中需要考虑的重要信息之 值(用与目标点之间的欧式距离来衡量),w(x)是当 一,因此,启发信息若能够考虑障碍物的位置信息将更 前节点x在局部环境中所受到的斥力总和的模长, 有前瞻性和可靠性,有利于机器人准确地判断下一步 aB、0是3个增益系数.当0=0时,f(x)为普通的 的动作.在保证路径长度较短的前提下,尽可能地靠近 启发函数,即与式(1)等价. 目标点及远离障碍物是路径规划最理想的状态,此处 采用式(3)作为启发函数,考虑到了机器人从 引入人工势场法(artificial potential field,APF)的思 传感器得到的障碍物位置信息,可以根据局部环境 想516,让机器人尽可能地避开障碍物.本文将一定范 信息的变化动态地修改启发函数,这将有利于规划 围内的障碍物对机器人产生的斥力作为一种惩罚函数 出更优的轨迹.此外,经过改进的启发函数仍然能够 添加至启发函数中.在人工势场法中斥力场公式为: 满足启发式搜索算法的可归纳性],即在一些问题 1 1-11x-X1, 2 的求解过程中,如果存在最短路径,无论在什么情况 Up 27 p Po p≤Pn: 之下,该搜索算法都能够保证找到这条最短路径. P Po. 启发函数中的系数选择将会影响到函数的最终 式中:m是正增益系数;X=(x,y,)和Xc=(xc,yc) 结果,从实验的角度分析系数的选择.选取α与B的 分别表示机器人位置向量和目标点位置向量;P表 最佳比例为骨=0B与日最佳的比例从多个指 1 示机器人到障碍物的欧式距离;表示单个障碍物影 响的最大距离范围相应的斥力为其负梯度,如式(2): 标(路径长度、方向转换次数、扩展的节点数和运行 1 111p 时间)进行分析.在500×500的栅格中,采用具有代 aK” p≤pn; 表性的启发式搜索算法一A·算法2]作为测试算 F=-grad(Up Po P Po 法,选择不同的B与日比例在500种随机环境下进 (2) 行路径规划,有效的平均数据统计如表1所示。 表1不同增益系数比例下规划的数据统计结果 Table 1 The calculation results of path planning in different gain factors 测试编号 8 路径长度/cm 转向次数 运行时间/3 经过的点数 B/0 1 0.0 1.0 291.3542 168.60 0.2967 252.0 2 0.1 0.1 388.4666 291.67 0.4134 311.0 1.0 3 0.2 0.2 388.4666 291.67 0.4134 311.0 1.0 0.1 0.2 394.5458 292.93 0.3891 301.0 2.0 0.3 0.6 394.5458 292.93 0.3891 301.0 2.0 6 0.1 0.3 355.6872 273.72 0.3834 299.0 3.0 > 0.4 1.2 355.6875 273.71 0.3834 299.0 3.0 0.1 0.4 324.8753 246.25 0.3700 283.0 4.0 0.1 0.5 300.9753 205.56 0.3226 267.0 5.0 o 0.1 0.6 281.6467 167.01 0.3011 253.0 6.0 0.1 0.7 282.5632 167.21 0.2623 249.0 7.0 1 0.1 0.8 285.8882 170.64 0.2857 250.0 8.0 0.1 0.9 289.6234 172.56 0.2990 253.0 9.0 1 0.1 1.0 295.7580 180.26 0.3544 277.0 10.0 0.1 1.1 295.7580 180.26 0.3544 277.0 11.0 16 0.1 1.2 295.7580 180.26 0.3544 277.0 12.0 从表1的数据统计可以得出以下结论:1)采用 同一比例的不同B与0值规划后的轨迹基本一致;

第1期 肖国宝,等:一种基于改进Theta'的机器人路径规划算法 ·61 2)合理地将障碍物信息引入到启发函数后,可以得 到B9的线段,但E1不会成为B9的父节点,路径经过了 到更优的路径(当0=0时,A·算法采用的是普通的启 点C6.分析其原因在于Basic Theta的扩展方式[B],即 发策略);3)当比例大于10时,各项数据指标趋于稳 2个顶点之间并不会随意形成父节点与子节点的关系 定;4)从多个指标衡量,最佳的比例为(/B)=(1/7). 6 8910 同样,采用其他启发式搜索算法作为测试算法,其数据 统计也能够反应出类似的趋势 1.3 Basic Theta*算法及其改进 Basic Theta算法是一种栅格路径规划算法,也 是A·算法的一种变种,其最大的改进在于它不要 求搜索树节点的父节点必须是其相邻的节点,因此 图5 Theta·算法规划轨迹演示 所求解路径的轨迹不限制在栅格的横向与纵向,理 Fig.5 The path planning demo of Theta'algorithm 论上允许以任意角度改变路径的方向[] 对路径进行平滑处理能够有效地优化路径20] 在估价函数的选取上,Basic Theta算法与A· 在经过Basic Theta*算法搜索找到路径后,中间经过 算法是一致的,故在使用其解决路径规划问题时,式 的点会大量减少,对其进一步平滑可以在较短的时 (3)作为其启发函数能够获取更优的路径.该算法 间内完成.具体平滑步骤如下. 在搜索中设置了2个表:OPEN表和CLOSE表. 1)获取Basic Theta规划后的路径轨迹节点集合 OPEN表保存了所有已扩展而未被考察过的节点, 2)选择集合中的起始点为平滑的基准点x。 CLOSE表记录了已被考察过的节点. 3)判断节点x与节点:是否相通,其中,节点z Basic Theta算法的步骤如下[9 为节点y的后续节点,节点y为节点x的后续节点: 1)初始化OPEN、CLOSE表,并将起始点S放入 ①若相通,去除中间节点y,即将节点x的后续节 到OPEN表中. 点修改为节点:,相应地,节点:的父节点为节点x; 2)如果OPEN表为空,表示没有找到路径,退出. ②否则,将基准点更新为节点y.如此循环,直 3)从OPEN表中找出最佳节点,作为当前节点 到节点y为目标点时,循环结束,转到4) x,并将其从OPEN表移到CLOSE表中 4)平滑完毕后,从目标点回溯到起始点,重新 4)判断当前节点x是否为目标点,如果是,则通 组成最佳的节点集合. 过节点x的父节点,一直遍历到起点,找到路径的节 由Basic Theta·算法与平滑步骤组成PS_The 点集合,搜索结束;否则,转至5) a算法,针对图5中Basic Theta算法规划的轨迹, 5)开始扩展当前节点x,找到当前节点的所有 PS_Theta算法能够进一步优化路径,如图6所示, 后续节点集合U并遍历集合内节点.如果遍历的节 光滑度是路径轨迹优越性的重要指标,光滑的轨迹 点y:不在OPEN或者CLOSE表中,将该节点y:加 能够有效提高机器人到达目标点的效率,可以尽可 入OPEN表中,计算该节点y:的估计值,并记录其 能地满足非完整性约束的条件」 父节点为x;否则,转至6). A 6 10 6)判断当前节点x的父节点x'与遍历的节点y 是否相通(节点之间的线段没有经过障碍物): ①若相通,比较当前节点的父节点x'的代价 D g(x)和OPEN表中的代价g(y:),如果g(x)较小, 则更新表中的代价,并将节点y:的父节点指向x'; ②若不相通,直接比较当前节点的代价g(x)和 图6PS_Theta·算法规划轨迹演示 OPEN表中的代价g(y:),如果g(x)较小,则更新表 Fig.6 The path planning demo of PS Theta'algorithm 中的代价及父节点 2 7)按照估价值递增顺序,对OPEN表中的节点 仿真与结果分析 进行排序,转向2) 2.1二维随机环境下的路径规划问题 Basic Theta算法能够突破格子的限制,找到可行 本文在Matlab7.6环境下对算法进行验证和比 路径,但该算法存在着一些缺陷,即最先找到的路径并 较.在二维环境下,采用本文提出的改进启发式搜索 不能保证路径最短.如图5所示,最短路径应该是E1 策略,对A·[】、Basic Theta[ia]与PS_Theta算法
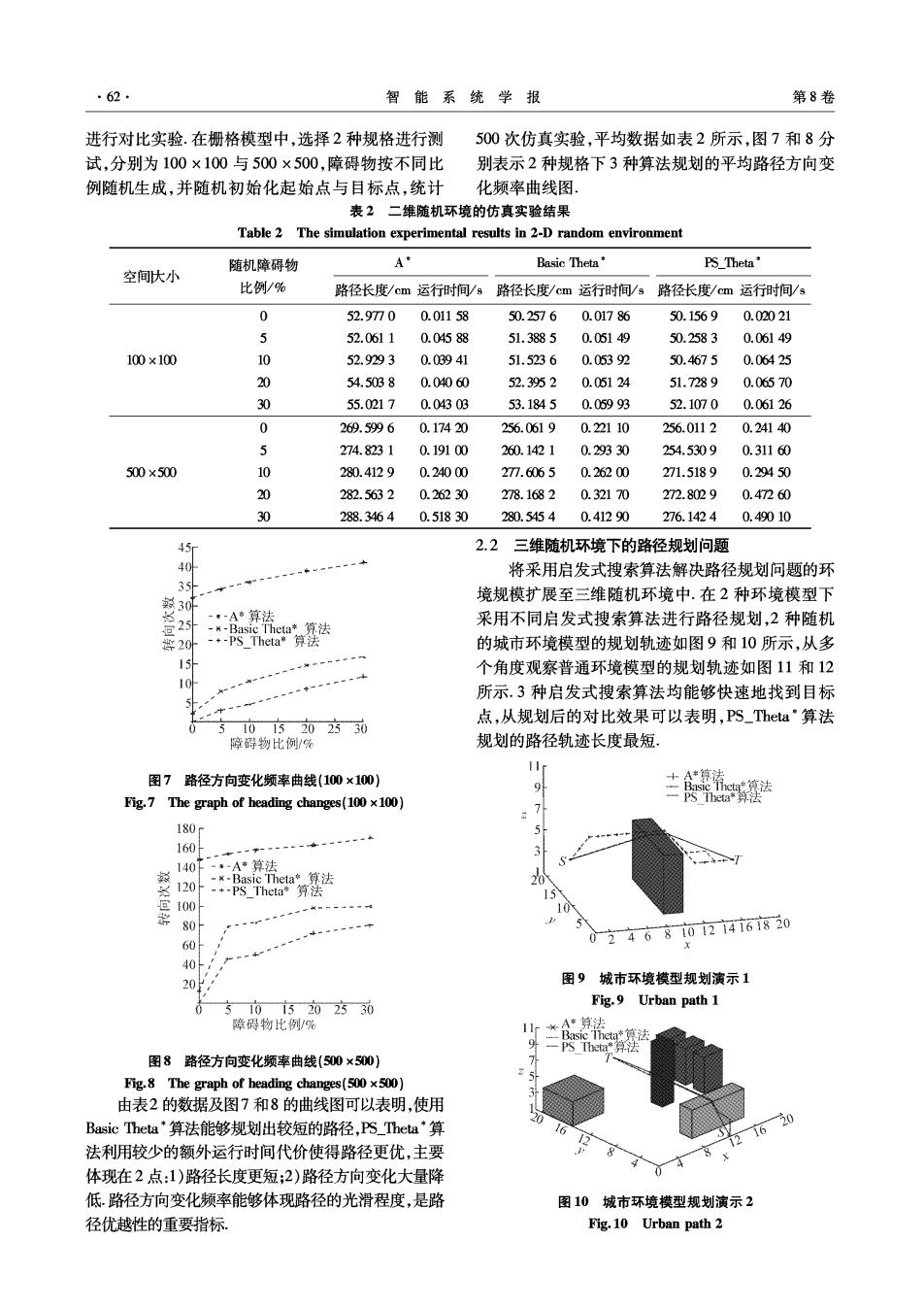
·62 智能系统学报 第8卷 进行对比实验.在栅格模型中,选择2种规格进行测 500次仿真实验,平均数据如表2所示,图7和8分 试,分别为100×100与500×500,障碍物按不同比 别表示2种规格下3种算法规划的平均路径方向变 例随机生成,并随机初始化起始点与目标点,统计 化频率曲线图, 表2二维随机环境的仿真实验结果 Table 2 The simulation experimental results in 2-D random environment 随机障碍物 A Basic Theta' PS Theta 空间大小 比例/% 路径长度/cm运行时间/s路径长度/cm运行时间/s路径长度/cm运行时间/s 0 52.970 0.01158 50.2576 0.01786 50.1569 0.02021 与 52.0611 0.04588 51.3885 0.05149 50.2583 0.06149 100×100 10 52.9293 0.03941 51.5236 0.05392 50.4675 0.06425 20 54.5038 0.04060 52.3952 0.05124 51.7289 0.06570 30 55.0217 0.04303 53.1845 0.05993 52.1070 0.06126 0 269.5996 0.17420 256.06190.22110 256.0112 0.24140 5 274.8231 0.19100 260.1421 0.29330 254.5309 0.31160 500×500 10 280.4129 0.24000 27.6065 0.26200 271.5189 0.29450 20 282.5632 0.26230 278.1682 0.32170 272.8029 0.47260 30 288.3464 0.51830 280.5454 0.41290 276.1424 0.49010 45m 2.2 三维随机环境下的路径规划问题 40H 将采用启发式搜索算法解决路径规划问题的环 35 30 境规模扩展至三维随机环境中.在2种环境模型下 2 --A多算法 采用不同启发式搜索算法进行路径规划,2种随机 -¥-Basic Theta*算法 20 -+-PS Theta* 算法 的城市环境模型的规划轨迹如图9和10所示,从多 个角度观察普通环境模型的规划轨迹如图11和12 以 所示.3种启发式搜索算法均能够快速地找到目标 点,从规划后的对比效果可以表明,PS_Theta·算法 1015202530 障碍物比例/% 规划的路径轨迹长度最短: 图7路径方向变化频率曲线(100×100) 9 het*法 Ffig.7 The graph of heading changes(100×100】 180 160 140下-·A*算法 -x-Basic Thetat*算法 120 -*-PS_Theta算法 5 100 10 群 80 60 0246810121416820 40 20 图9城市环境模型规划演示1 0 51015202530 Fig.9 Urban path 1 障碍物比例/% 11r 光A*算法 Basic Theta*算法 一PS Theta*算法 图8路径方向变化频率曲线(500×500) Fig.8 The graph of heading changes(500 x500) 由表2的数据及图7和8的曲线图可以表明,使用 Basic Theta算法能够规划出较短的路径,PS_Theta*算 20 16 法利用较少的额外运行时间代价使得路径更优,主要 体现在2点:1)路径长度更短;2)路径方向变化大量降 低.路径方向变化频率能够体现路径的光滑程度,是路 图10城市环境模型规划演示2 径优越性的重要指标。 Fig.10 Urban path 2