
本次课的内容 1平面力偶系的合成与平衡 2平面任意力系的简化 本次课的重点 1平面力偶系平衡的条件的应用 2平面任意力系简化的概念一主矢、主矩 3平面任意力系简化结果分析 本次课的难点 平面任意力系简化结果分析 31
31 本次课的内容 1 平面力偶系的合成与平衡 2 平面任意力系的简化 本次课的重点 1 平面力偶系平衡的条件的应用 2 平面任意力系简化的概念—主矢、主矩 本次课的难点 3 平面任意力系简化结果分析 平面任意力系简化结果分析

2.2平面力对点的矩平面力偶 三力偶的性质 性质1:力偶不能合成为一个力,不能用一个力来平衡 性质2:力偶对其作用面内任一点的矩恒等于力偶矩,而 与矩心的选取无关 M(F.F) =F(d+x)-F'x F-F 所以 M(F.F)=Fd B 性质2得到证明 32
32 三 力偶的性质 = F(d + x) 性质1:力偶不能合成为一个力,不能用一个力来平衡 性质2:力偶对其作用面内任一点的矩恒等于力偶矩,而 与矩心的选取无关 F F' d D A B C O M (F, F') M (F, F') = Fd F x ' − ' F = F 所以 x 性质2得到证明 2.2 平面力对点的矩 平面力偶
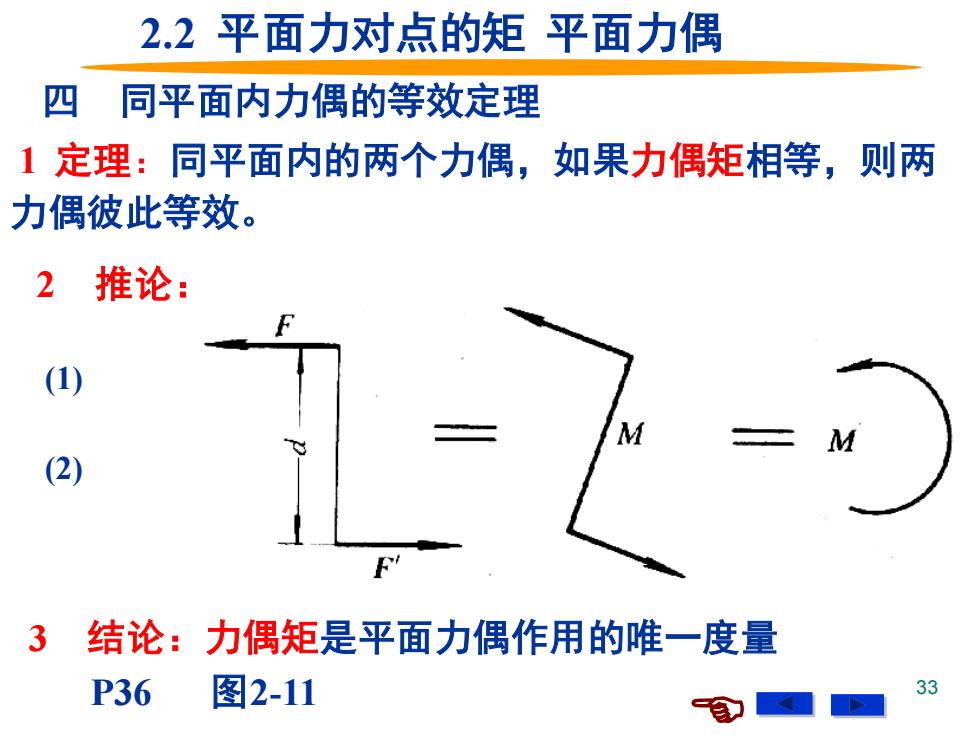
2.2平面力对点的矩平面力偶 四同平面内力偶的等效定理 1定理:同平面内的两个力偶,如果力偶矩相等,则两 力偶彼此等效。 推论: 2 (1) (2) 3 结论:力偶矩是平面力偶作用的唯一度量 P36 图2-11 33
33 四 同平面内力偶的等效定理 1 定理:同平面内的两个力偶,如果力偶矩相等,则两 力偶彼此等效。 2 推论: (1) (2) 3 结论:力偶矩是平面力偶作用的唯一度量 2.2 平面力对点的矩 平面力偶 P36 图2-11
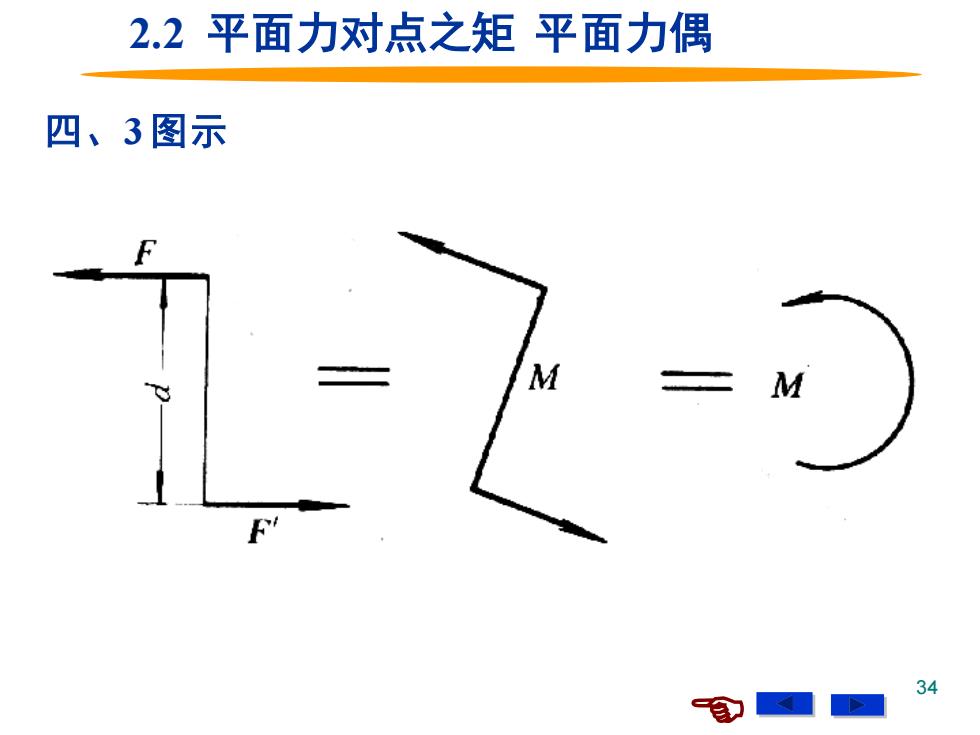
2.2平面力对点之矩平面力偶 四、3图示 M 34
34 四、3 图示 2.2 平面力对点之矩 平面力偶

2.2平面力对点之矩平面力偶 五平面力偶系的合成与平衡条件 1合成 在同平面内的任意个力偶可以合成为一个合力偶, 合力偶矩等于各个力偶矩的代数和/ M=∑M, 2平衡条件M=∑M,=0 i=1 六平衡条件的应用 1取研究对象 2受力图? 3列方程? 4求解 35
35 1 合成 在同平面内的任意个力偶可以合成为一个合力偶, 1 n i i M M = = 五 平面力偶系的合成与平衡条件 2 平衡条件 合力偶矩等于各个力偶矩的代数和 2.2 平面力对点之矩 平面力偶 六 平衡条件的应用 1 取研究对象 2 受力图? 3 列方程? 4 求解 1 n i i M M = = =0