
The Shortest Path Problem ● Let G=(,E)be a directed graph in which each edge has a nonnegative length,and a distinguished vertex s called the source.The single-source shortest path problem,or simply the shortest path problem,is to determine the distance from s to every other vertex in where the distance from vertex s to vertex xis defined as the length of a shortest path from sto x. For simplicity,we will assume that V1,2,...,n) and s=1. This problem can be solved using a greedy technique known as Dijkstra's algorithm
The Shortest Path Problem ◼ Let G=(V, E) be a directed graph in which each edge has a nonnegative length, and a distinguished vertex s called the source. The single-source shortest path problem, or simply the shortest path problem, is to determine the distance from s to every other vertex in V, where the distance from vertex s to vertex x is defined as the length of a shortest path from s to x. ◼ For simplicity, we will assume that V={1, 2, …, n} and s=1. ◼ This problem can be solved using a greedy technique known as Dijkstra’s algorithm

The Shortest Path Problem The set of vertices is partitioned into two sets x and yso that Xis the set of vertices whose distance from the source has already been determined,while ycontains the rest vertices. Thus,initially =1}and Y=2,3,...,n. Associated with each vertex yin Yis a label[☑, which is the length of a shortest path that passes only through vertices in X.Thus,initially if(L,i)∈E 0=0, 2≤i≤n if(1,iE
The Shortest Path Problem ◼ The set of vertices is partitioned into two sets X and Y so that X is the set of vertices whose distance from the source has already been determined, while Y contains the rest vertices. Thus, initially X={1} and Y={2, 3, …, n}. ◼ Associated with each vertex y in Y is a label [y], which is the length of a shortest path that passes only through vertices in X. Thus, initially length 1, if (1, ) ( ) [1] 0, [ ] , 2 if (1, ) i i E i i n i E = =

The Shortest Path Problem a At each step,we select a vertex ve ywith minimum 1 and move it to x,and a of each vertex we ythat is adjacent to yis updated indicating that a shorter path to wvia yhas been discovered. VwEY and (y,w)EE,[w]=min(w],y]+length(y,w) The above process is repeated until Yis empty. Finally,1 of each vertex in Xis the distance from the source vertex to this one
The Shortest Path Problem ◼ At each step, we select a vertex yY with minimum and move it to X, and of each vertex wY that is adjacent to y is updated indicating that a shorter path to w via y has been discovered. = + w Y y w E w w y y w and , , [ ] min [ ], [ ] length , ( ) ( ) ◼ The above process is repeated until Y is empty. ◼ Finally, of each vertex in X is the distance from the source vertex to this one
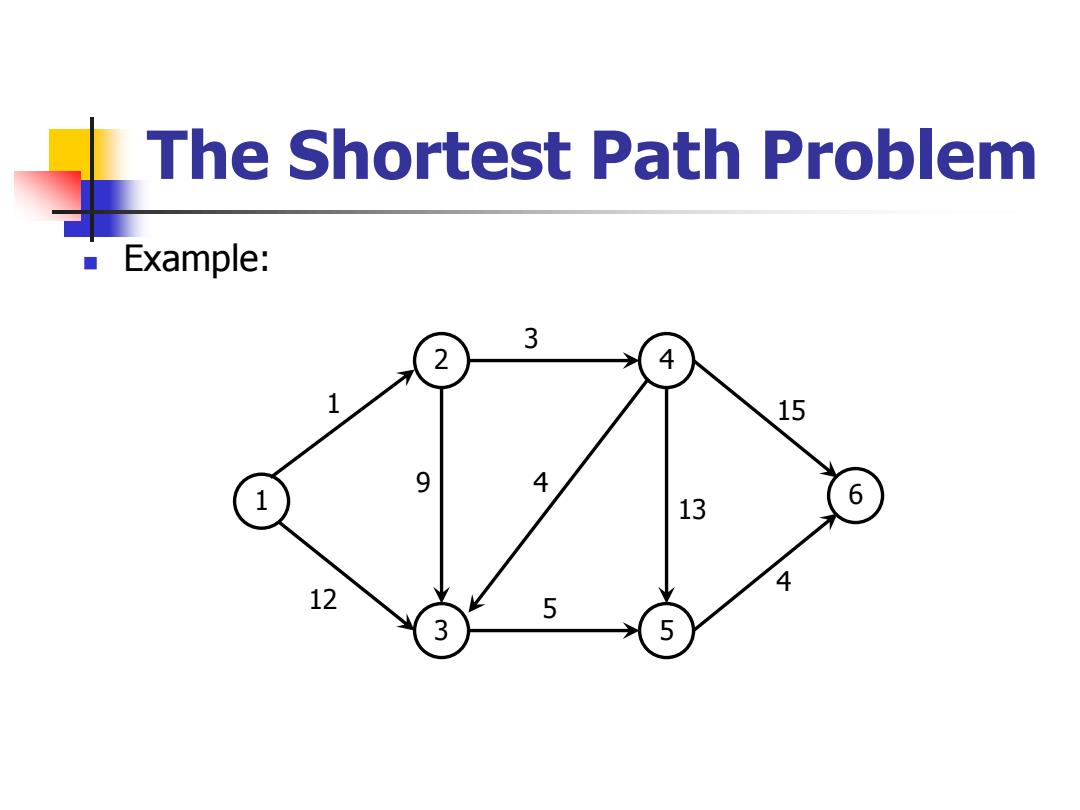
The Shortest Path Problem Example: 3 2 4 1 15 9 4 1 13 6 4 12 5 3 5
The Shortest Path Problem ◼ Example: 1 2 3 4 5 6 1 12 9 3 4 5 13 15 4

The Shortest Path Problem Input:A weighted directed graph G=(E),where V1,2,...,; Output:The distance from vertex 1 to every other vertex in G; 1.={1;-{1;[1]←-0; ■ 2.for v2 to n ■ 3. if yis adjacent to1 then 2[☑k--length1,☑; ■ 4. else [y☑k-o; ■ 5. end if; 6.end for; 7.for六-1tor1 ■ 8. Let ye ybe such that a[y]is minimum; 9. Xxoy);//add vertex ytoX 10. Yy);//delete vertex yfrom Y 11. for each edge (y,w) 12. if we Yand i[y]+lengthly,w]<a[w]then 13. 2[M←-[☑+ength[y,WM: 14 end for; ■ 15. end for;
The Shortest Path Problem ◼ Input: A weighted directed graph G=(V, E), where V={1, 2, …, n}; ◼ Output: The distance from vertex 1 to every other vertex in G; ◼ 1. X={1}; YV-{1}; [1]0; ◼ 2. for y2 to n ◼ 3. if y is adjacent to 1 then [y]length[1, y]; ◼ 4. else [y]; ◼ 5. end if; ◼ 6. end for; ◼ 7. for j1 to n-1 ◼ 8. Let yY be such that [y] is minimum; ◼ 9. XX{y}; //add vertex y to X ◼ 10. YY-{y}; //delete vertex y from Y ◼ 11. for each edge (y, w) ◼ 12. if wY and [y]+length[y, w]<[w] then ◼ 13. [w][y]+length[y, w]; ◼ 14. end for; ◼ 15. end for;