
Preliminaries A tree can be defined in several ways.One natural way to define a tree is recursively. A tree is a collection of nodes.The collection can be empty;otherwise,a tree consists of a distinguished node r,called the root and zero or more nonempty (sub)trees 71,72....,7k each of whose roots are connected by a directed edge from / The root of each subtree is said to be a child of, and ris the parent of each subtree root. root 方 万五 万 Ta Tio
Preliminaries ◼ A tree can be defined in several ways. One natural way to define a tree is recursively. ◼ A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty (sub)trees T1 , T2 , …, Tk , each of whose roots are connected by a directed edge from r. ◼ The root of each subtree is said to be a child of r, and r is the parent of each subtree root. root T1 T2 T3 T4 … T10
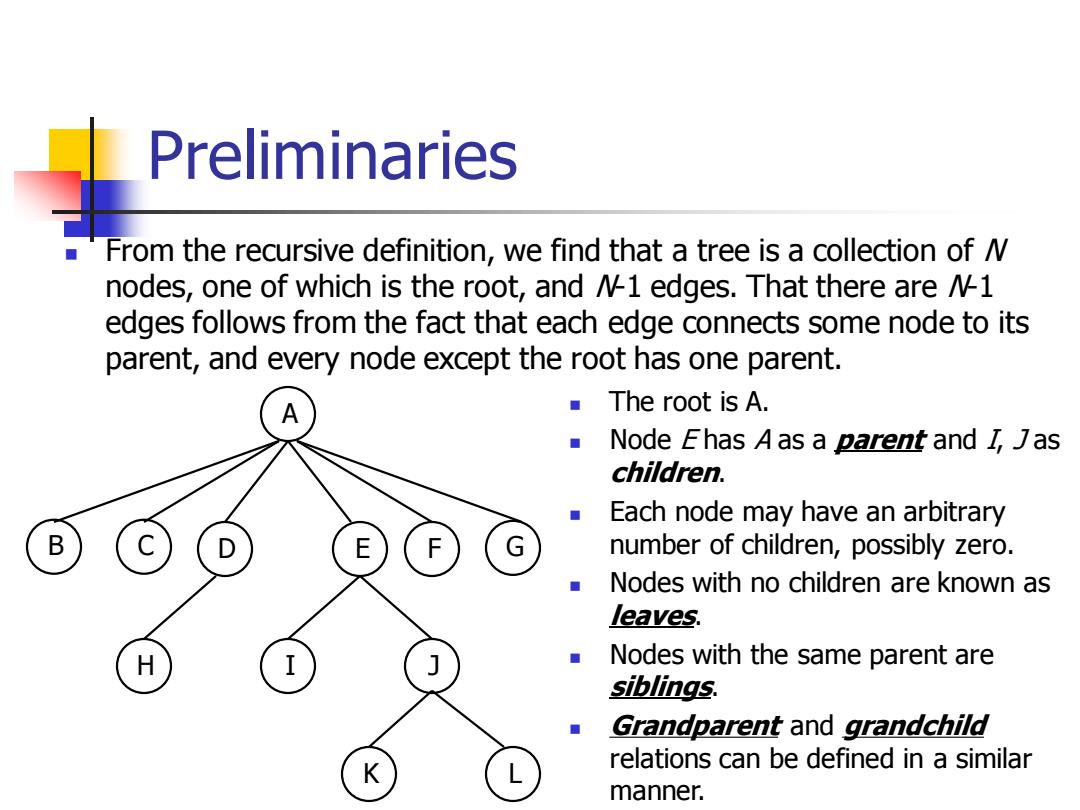
Preliminaries From the recursive definition,we find that a tree is a collection of nodes,one of which is the root,and /1 edges.That there are /1 edges follows from the fact that each edge connects some node to its parent,and every node except the root has one parent. A The root is A. Node Fhas A as a parent and I,Jas children. Each node may have an arbitrary B E number of children,possibly zero. Nodes with no children are known as leaves. H I J Nodes with the same parent are siblings. Grandparent and grandchild K relations can be defined in a similar manner
Preliminaries ◼ From the recursive definition, we find that a tree is a collection of N nodes, one of which is the root, and N-1 edges. That there are N-1 edges follows from the fact that each edge connects some node to its parent, and every node except the root has one parent. A B C D E F G H I J K L ◼ The root is A. ◼ Node E has A as a parent and I, J as children. ◼ Each node may have an arbitrary number of children, possibly zero. ◼ Nodes with no children are known as leaves. ◼ Nodes with the same parent are siblings. ◼ Grandparent and grandchild relations can be defined in a similar manner

Preliminaries A path from node n to n is defined as a sequence of nodes m,n,n...,nk such that n is the parent of n for 1≤Kk The length of this path is the number of edges on the path,namely k1.There is a path of length zero from every node to itself.Notice that in a tree there is exactly one path from the root to each node
Preliminaries ◼ A path from node n1 to nk is defined as a sequence of nodes n1 , n2 , n3…, nk such that ni is the parent of ni+1 for 1i<k. ◼ The length of this path is the number of edges on the path, namely k-1. There is a path of length zero from every node to itself. Notice that in a tree there is exactly one path from the root to each node

Preliminaries For any node n the depth of n;is the length of the unique path from the root to /,Thus,the root is at depth 0.The height of n,is the length of the longest path from n,to a leaf.Thus all leaves are at height 0.The height of a tree is equal to the height of the root.The depth of a tree is equal to the depth of the deepest leaf;this is always equal to the height of the tree. If there is a path from m to m,then m is an ancestor of m and m is a descendant of m.If mtm,then m is a proper ancestor of m and m is a proper descendant of m
Preliminaries ◼ For any node ni , the depth of ni is the length of the unique path from the root to ni . Thus, the root is at depth 0. The height of ni is the length of the longest path from ni to a leaf. Thus all leaves are at height 0. The height of a tree is equal to the height of the root. The depth of a tree is equal to the depth of the deepest leaf; this is always equal to the height of the tree. ◼ If there is a path from n1 to n2 , then n1 is an ancestor of n2 and n2 is a descendant of n1 . If n1n2 , then n1 is a proper ancestor of n2 and n2 is a proper descendant of n1
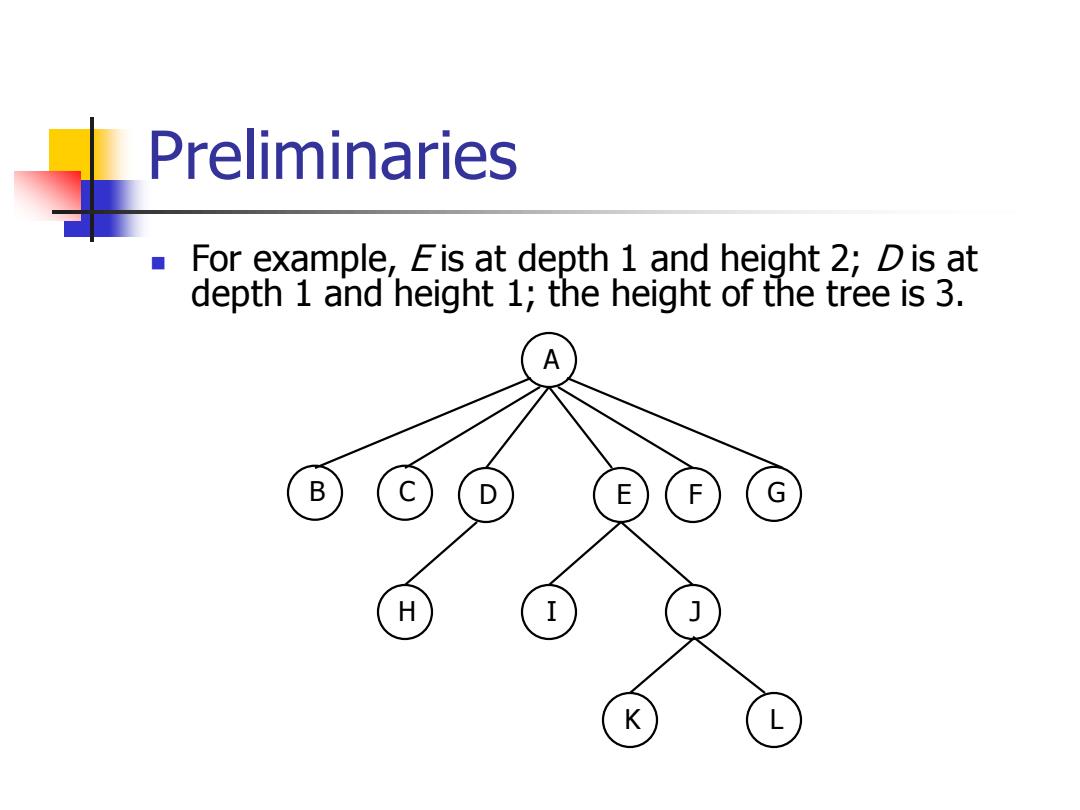
Preliminaries For example,Eis at depth 1 and height 2;Dis at depth 1 and height 1;the height of the tree is 3. A B D E G H I J K
Preliminaries ◼ For example, E is at depth 1 and height 2; D is at depth 1 and height 1; the height of the tree is 3. A B C D E F G H I J K L