
2.1.3. 汇交力系的平衡条件 F2 n FR=回,F=0 i=1 几何形式:力多边形封闭 解析形式: ∑F=0 ∑F=0 ∑F=0 FR=(FR)+(F)+(FR)2
2.1.3. 汇交力系的平衡条件 ◼ 解析形式: FR = Fi=0 i=1 n F 1 B F 2 C F 3 D F 4 E A F 5 ⚫几何形式:力多边形封闭 FR F 1 B F 2 C F 3 D F 4 E A
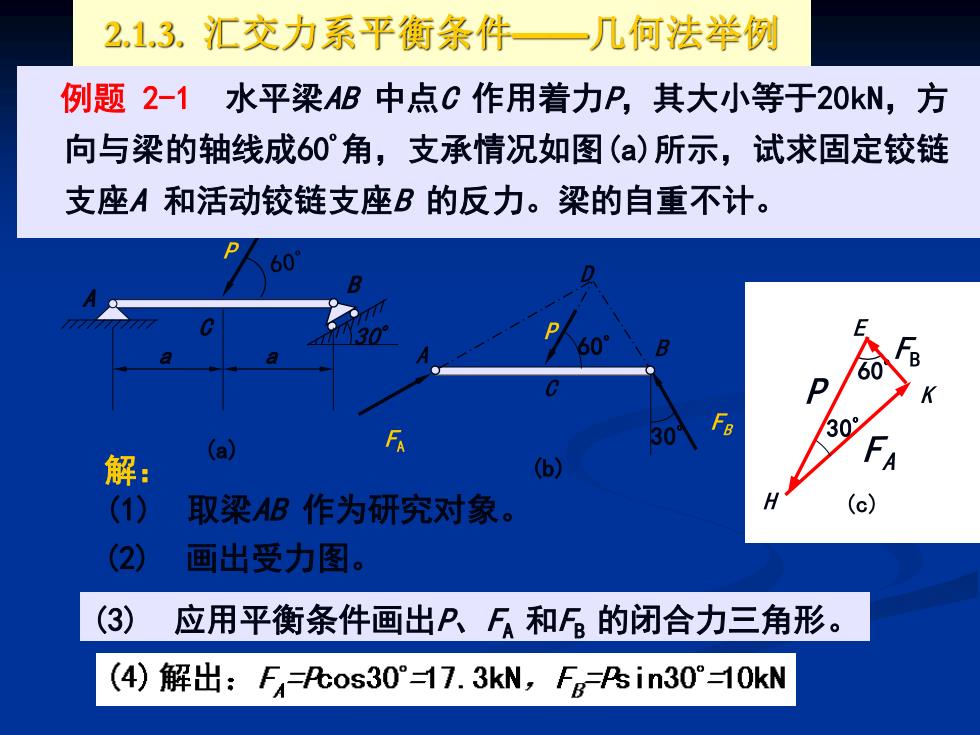
2.1,3.汇交力系平衡条件一几何法举例 例题2-1水平梁AB中点C作用着力P,其大小等于20kN,方 向与梁的轴线成60°角,支承情况如图()所示,试求固定铰链 支座A和活动铰链支座B的反力。梁的自重不计。 60 E 601 B 50 30 (a) 解: (1) 取梁B作为研究对象。 (c) (2 画出受力图。 (3) 应用平衡条件画出PF和F的闭合力三角形。 (4)解出:Fos30°=17.3kN,FAin30°-10kN
60º 30º A B 30 º a a C (a) (b) 60º 30º 解: (1) 取梁AB 作为研究对象。 (2) 画出受力图。 (3) 应用平衡条件画出P、FA 和FB 的闭合力三角形。 例题 2-1 水平梁AB 中点C 作用着力P,其大小等于20kN,方 向与梁的轴线成60º角,支承情况如图(a)所示,试求固定铰链 支座A 和活动铰链支座B 的反力。梁的自重不计。 2.1.3. 汇交力系平衡条件——几何法举例

主矢一汇交力系求合力举例 例2-2如图2-8所示,作用于吊环螺钉上的四个力F1,F,F:和F构成平面汇交 力系.已知各力的大小和方向为耳=360,=60°,耳3=550,为=0°, 至3=380N,s=30°;R=300N,4=70°.试用解析法求合力的大小和方向. FR=VE)子+()2+(F)月 1=60 F.=∑Fcosa, FR =Fix+Fx+Fsx +F4 必3=300 4=70°、F Fav=∑sina, =Fix+Fx+F3x+Fay 图28解析法求力系合力
主矢—汇交力系求合力举例

F Rx =360.c0s60°+550+380c0s30+300.c0s70 =1161.7N) =360.sin60°+0380.sin30°-300.sin70° =-160.13(N) F=V(E)P+(Rv尸=117268N 01=609 合力与x轴的夹角 F 03-30° tana 2,=-7°50 a4=70°F
合力与x轴的夹角
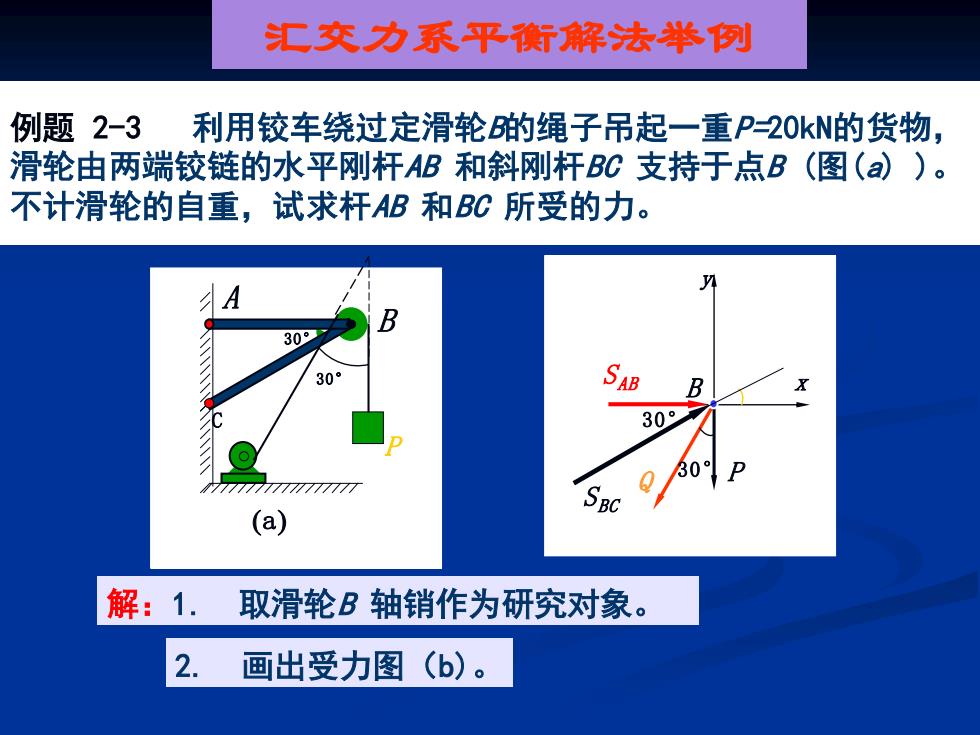
汇交力系平守解法举例 例题2-3 利用铰车绕过定滑轮的绳子吊起一重P20kN的货物, 滑轮由两端铰链的水平刚杆AB和斜刚杆BC支持于点B(图(a))。 不计滑轮的自重,试求杆AB和BC所受的力。 A B 30° 30° SAB B 30 77777777777777 (a) 解:1. 取滑轮B轴销作为研究对象。 2. 画出受力图(b)
解:1. 取滑轮B 轴销作为研究对象。 2. 画出受力图(b)。 例题 2-3 利用铰车绕过定滑轮B的绳子吊起一重P=20kN的货物, 滑轮由两端铰链的水平刚杆AB 和斜刚杆BC 支持于点B (图(a) )。 不计滑轮的自重,试求杆AB 和BC 所受的力。 汇交力系平衡解法举例 S BC Q S AB P x y 30° 30° (b) B 30° B P A C 30° (a)