
有限元理论与建模方法 Finite Element Analysis and Modeling 二、网格疏密 relative density) a) b) Elements:132 Elements:84 Max.stress:300.60MPa Max.stress:296.36MPa 电子科技大学机械与电气工程学院 2019,10
有限元理论与建模方法 电子科技大学机械与电气工程学院 Finite Element Analysis and Modeling 2019,10 二、网格疏密 ( relative density) Elements: 132 Max.stress: 300.60MPa Elements: 84 Max.stress: 296.36MPa

有限元理论与建模方法 Finite Element Analysis and Modeling 二、网格疏密 relative density) 应力集中区域,应力变化梯度大 电子科技大学机械与电气工程学院 2019,10
有限元理论与建模方法 电子科技大学机械与电气工程学院 Finite Element Analysis and Modeling 2019,10 二、网格疏密 ( relative density) 应力集中区域,应力变化梯度大
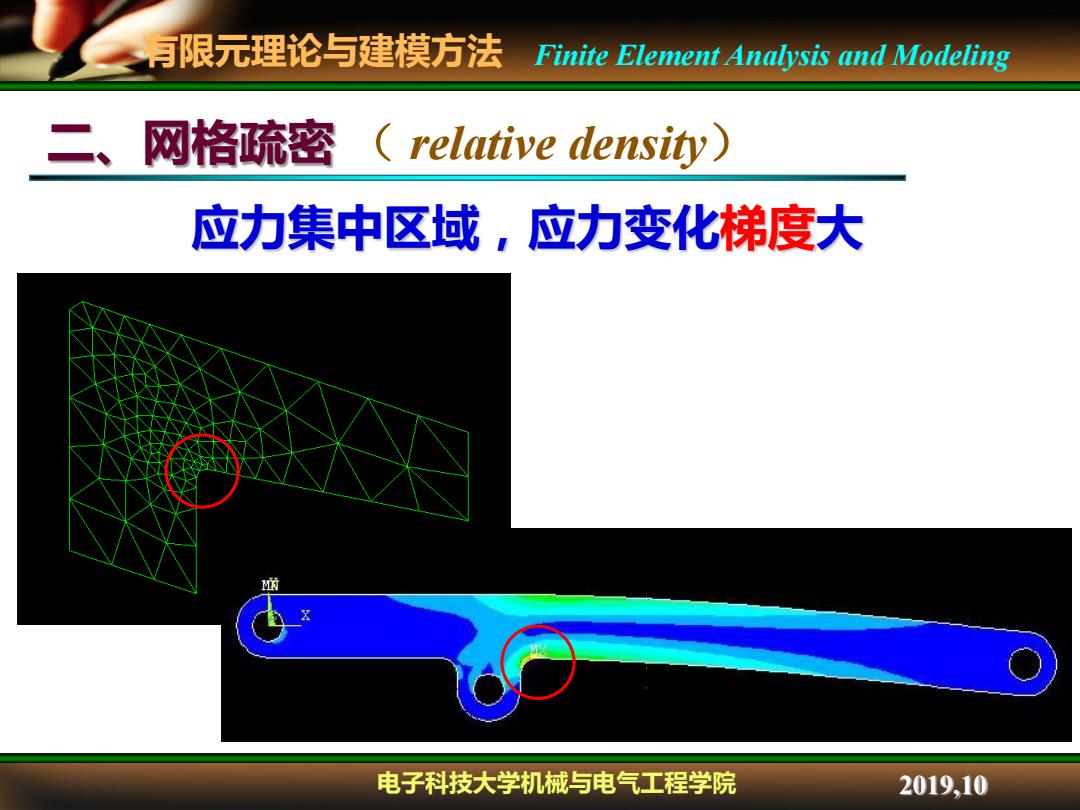
有限元理论与建模方法 Finite Element Analysis and Modeling 二、网格疏密 (relative density) 应力集中区域,应力变化梯度大 电子科技大学机械与电气工程学院 2019,10
有限元理论与建模方法 电子科技大学机械与电气工程学院 Finite Element Analysis and Modeling 2019,10 二、网格疏密 ( relative density) 应力集中区域,应力变化梯度大
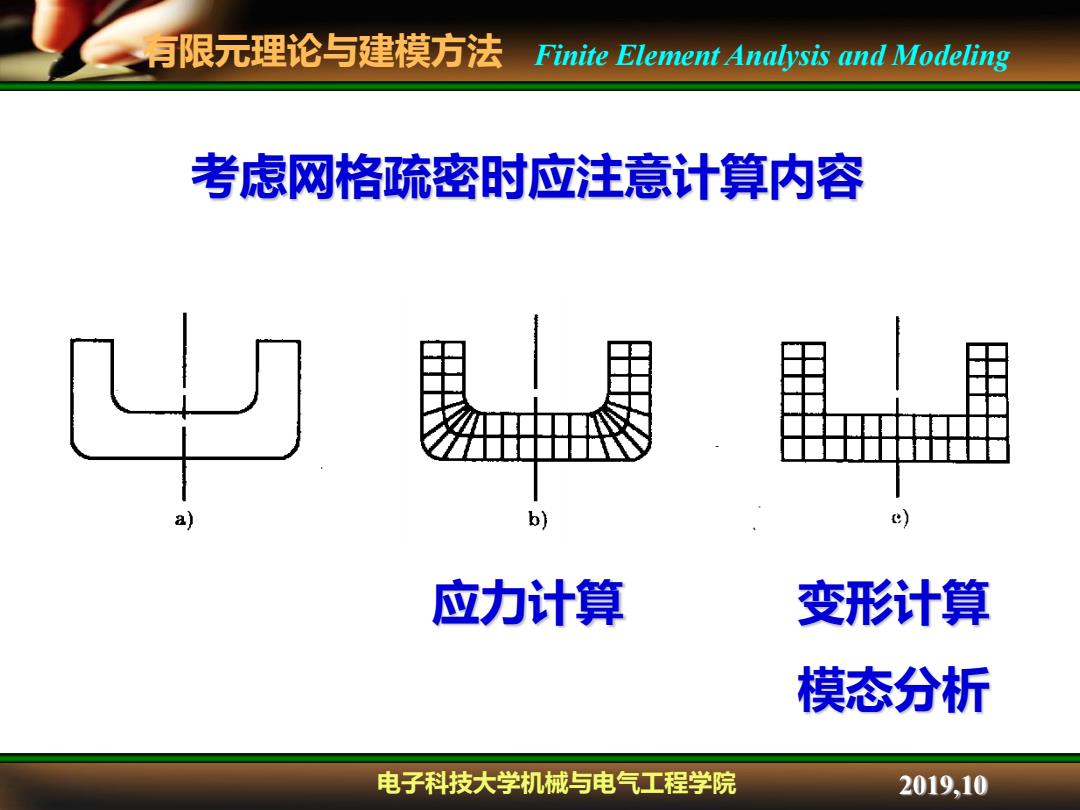
有限元理论与建模方法 Finite Element Analysis and Modeling 考虑网格疏密时应注意计算内容 b) c) 应力计算 变形计算 模态分析 电子科技大学机械与电气工程学院 2019,10
有限元理论与建模方法 电子科技大学机械与电气工程学院 Finite Element Analysis and Modeling 2019,10 应力计算 变形计算 模态分析 考虑网格疏密时应注意计算内容
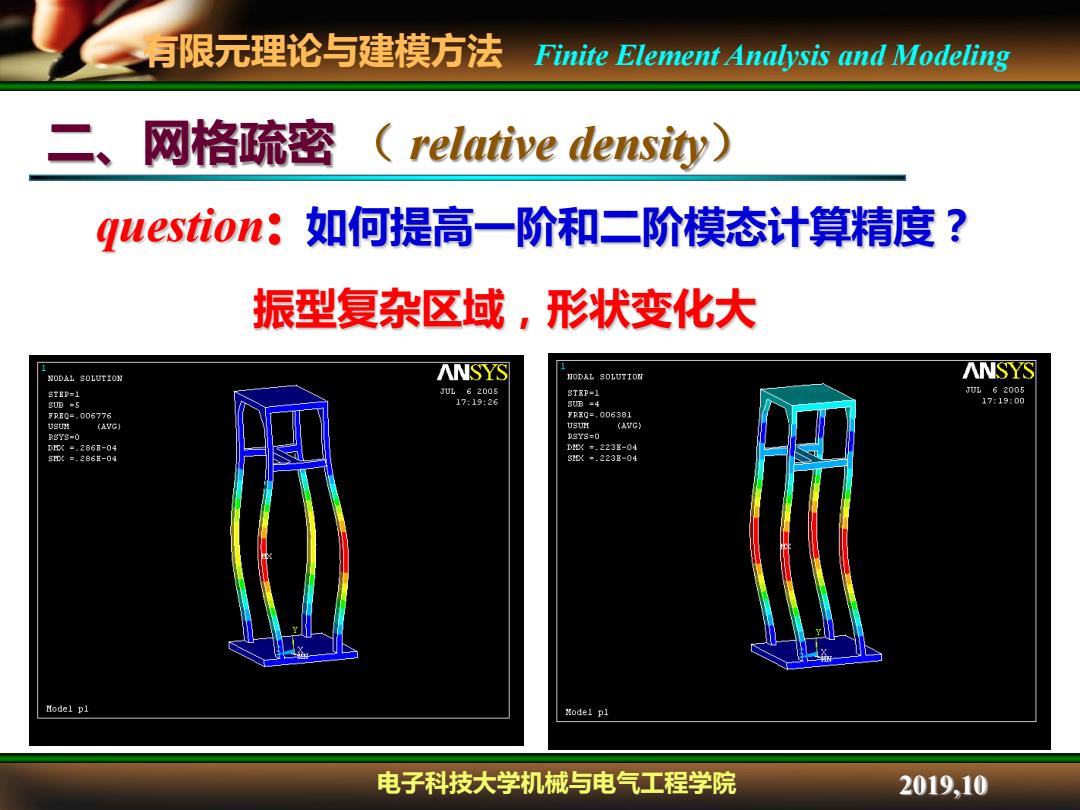
有限元理论与建模方法 Finite Element Analysis and Modeling 二、网格疏密 relative density) question:如何提高一阶和二阶模态计算精度? 振型复杂区域,形状变化大 NODAL S0 LUTI0因 ANSYS ANSYS rEP=】 3UL.62005 STEP-1 JU62005 日=5 17:19:26 8UB=4 17:19:00 FR80=,.006776 7Rx0=,006381 Dsu (AUC) RSYS-0 DSYS=0 D=.266-0 0以-.223E-04 gr以=,286B-04 g0X·.223E-04 Model pl Model pl 电子科技大学机械与电气工程学院 2019,10
有限元理论与建模方法 电子科技大学机械与电气工程学院 Finite Element Analysis and Modeling 2019,10 二、网格疏密 ( relative density) 振型复杂区域,形状变化大 question:如何提高一阶和二阶模态计算精度?