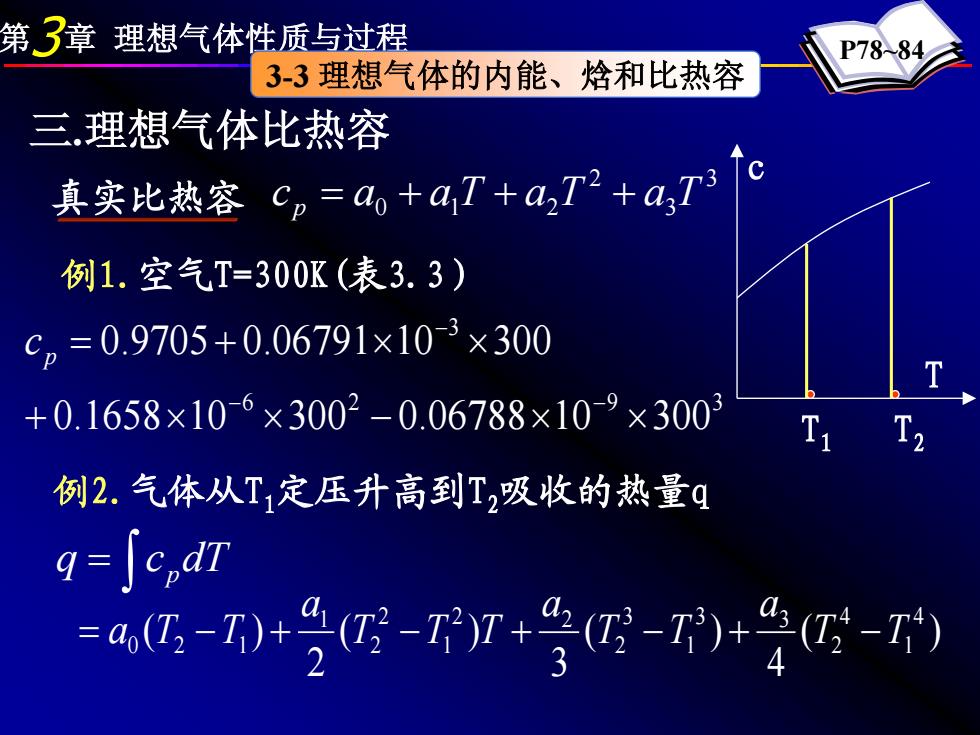
第3章理想气体性质与过程 P78-84 3-3理想气体的内能、焓和比热容 三理想气体比热容 真实比热容C,=a+a,7+a,72+a,7e 例1.空气T=300K(表3.3) cp=0.9705+0.06791×10-3×300 +0.1658×10-6×3002-0.06788×10-9×3003 T T2 例2.气体从T1定压升高到T2吸收的热量q q=Se,dT =a.-7+20-71+g-7+4-1)
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 三.理想气体比热容 3 3 2 真实比热容 c p = a0 + a1 T + a2T + a T T c T1 T2 例1.空气T=300K(表3.3) 6 2 9 3 3 0.1658 10 300 0.06788 10 300 0.9705 0.06791 10 300 + × × − × × = + × × − − − p c 例2.气体从T1定压升高到T2吸收的热量q ∫ q = c pdT ( ) 4 ( ) 3 ( ) 2 ( ) 4 1 4 2 3 3 1 3 2 2 2 1 2 2 1 0 2 1 T T a T T a T T T a = a T −T + − + − + −

第3章理想气体性质与过程 P7884 3-3理想气体的内能、焓和比热容 三理想气体比热容 真实比热容Cp=a+a,T+a2T2+a,T 例3.定容比热容C,=(a-R)+aT+a,T2+a,T3 平均比热容 p t 定义 l"c,dt pt灯 t2-t1 c." t2-t1 定压过程q=c,(-) 定容过程q=c,(化,-1)
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 三.理想气体比热容 3 3 2 真实比热容 c p = a0 + a1 T + a2T + a T 例3.定容比热容 3 3 2 0 1 2 cv = (a − R) + a T + a T + a T 平均比热容 2 1 2 1 ~ , , 1 2 t p t t v t t t c c 定义 2 1 2 2 1 1 t t c dt c t t v t v t − = ∫ 2 1 2 2 1 1 t t c dt c t t p t p t − = ∫ 定压过程 ( ) 2 1 2 1 q c t t t = p t − 定容过程 ( ) 2 1 2 1 q c t t t = v t −

第3章理想气体性质与过程 P7884 3-3理想气体的内能、焓和比热容 三理想气体比热容 平均比热容4~t2,C听,Cp 工程规定:以0C为基准 70 附表3、4、5、6 (~t2平均比热容 c264-c64 若以0K为基准 t2-t1 ,dT g-67-c57 Z-T 注意: cc,月
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 三.理想气体比热容 平均比热容 2 1 2 1 ~ , , 1 2 t p t t v t t t c c 工程规定:以0oC为基准 附表3、4、5、6 1 ~ 2 t t 平均比热容 2 1 0 2 0 1 2 1 2 1 t t c t c t c t p t p t p t − ⋅ − ⋅ = 若以0K为基准 注意: T p t p c c 0 = 0 2 1 2 1 T p T t p t ? c ?= c t c dt c t p t p ∫ = 0 0 t c dt c t v t v ∫ = 0 0 T c dT c T p T p ∫ = 0 0 2 1 0 2 0 1 2 1 2 1 T T c T c T c T p T T p p T − ⋅ − ⋅ = t p c 0

第3章理想气体性质与过程 P7884 3-3理想气体的内能、焓和比热容 三理想气体比热容 定值比热容温度较低时(25℃),原子处于振动基态能 级,不考虑振动,则单原子分子的平均动能(能量均分 定律:温度平衡,气体分子每个自由度平均动能都相等, 且等于kT/2.) k:波尔兹曼常数1.38x10-23JK Ng:阿伏加德罗常数6.022×1023/mol 内能3RmT/2→Cm=3Rm/2 1kmo1:单原子气体 焓5RnT/2→Cm=5R/2
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 三.理想气体比热容 定值比热容 kT 2 3 级,不考虑振动,则单原子分子的平均动能(能量均分 定律:温度平衡,气体分子每个自由度平均动能都相等, 且等于kT/2.) N k T RmT 2 3 ( ) 2 3 0 = 1kmol气体 k:波尔兹曼常数 23 1 1.38 10 . − − × J K N0:阿伏加德罗常数6.022 10 / mol 23 × 1kmol:单原子气体 内能 3R T / 2 m 焓 5R T / 2 m 温度较低时(25oC),原子处于振动基态能 3 / 2 Cvm = Rm 5 / 2 Cpm = Rm