
第3章理想气体性质与过程 P7577 3-2气体的比热容 定容比热容c, c,=(/dT) u=7,)=d=( 7+0-=a+n购 函-.n+p 比热容说明 ①定压过程中,△h=c,dI 可以测量。 ②定容过程中,△u=c,dT可以测量
第3章 理想气体性质与过程 P75~77 3-2 气体的比热容 定容比热容cv v v c = (δq / dT) δq = du + pdv u = u(T,v) dv v u dT T u du v T ( ) ( ) ∂ ∂ + ∂ ∂ = p dv v u dT T u q v T ( ) [( ) + ] ∂ ∂ + ∂ ∂ v v v δ = T u dT q c ( ) ( ) ∂ ∂ = = δ 比热容说明 ①定压过程中, ∫ ∆h = c pdT 可以测量。 ②定容过程中, ∫ ∆u = cvdT 可以测量

第了章理想气体性质与过程 P7884 33理想气体的内能、焓和比热容 一.理想气体内能和焓的特性 焦耳实验 1843年焦耳实验:理想气 夏空 体真空膨胀 实验结果:p!v↑T不变 绝热自由膨胀 结采分折:Q=心,-+W号光U:=心 g=p咖=学.+岁中多=0 理想气体内能与压力无关 u=u(T,v)→du=( ,--0 理想气体内能与比容无关
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 焦耳实验 一.理想气体内能和焓的特性 绝热自由膨胀 A B 1843年焦耳实验:理想气 真空 体真空膨胀 实验结果:p v T 不变 结果分析:Q =U2 −U1 +W 0 0 = = W Q U2 =U1 u = u(T, p) dp p u dT T u du p T ( ) ( ) ∂ ∂ + ∂ ∂ = 0 0 ≠ = dp dT ( ) = 0 ∂ ∂ T p u u = u(T,v) dv v u dT T u du p T ( ) ( ) ∂ ∂ + ∂ ∂ = 0 0 ≠ = dv dT ( ) = 0 ∂ ∂ T v u 理想气体内能与压力无关 理想气体内能与比容无关

第了章理想气体性质与过程 P7884 3-3理想气体的内能、焓和比热容 一理想气体内能和焓的特性 焦耳实验 1843年焦耳实验:理想气体 真空 真空膨胀 绝热自由膨胀 结论:u=u(T)理想气体内能是温度的单值函数 h=u+pv→h=u+RT=h(T) 理想气体焓是温度的单值函数 u=u(T),h=h(T)物理解释分子之间没有作用力,内位能零 理想气体比热容特性 dh du dT dT
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 焦耳实验 一.理想气体内能和焓的特性 绝热自由膨胀 A B 1843年焦耳实验:理想气体 真空 真空膨胀 结论: u = u(T) h = u + pv h = u + RT = h(T) 理想气体内能是温度的单值函数 理想气体焓是温度的单值函数 u=u(T),h=h(T)物理解释分子之间没有作用力,内位能零 理想气体比热容特性 dT du c dT dh c p = , v =
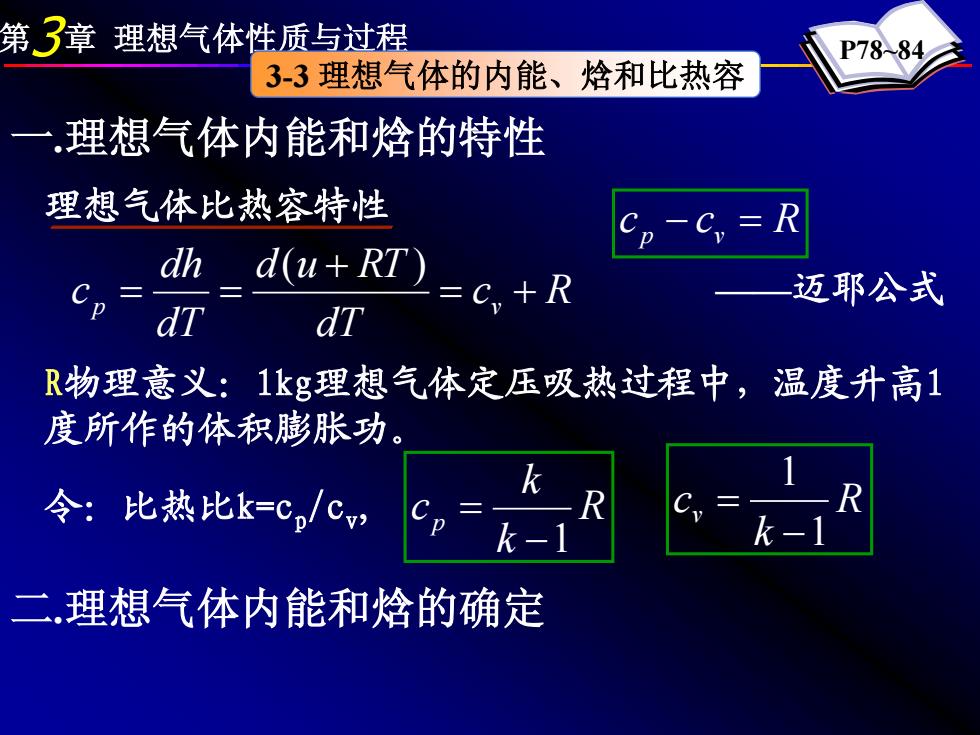
第了章理想气体性质与过程 P78-84 3-3理想气体的内能、焓和比热容 一理想气体内能和焓的特性 理想气体比热容特性 -C,=R dh d(u+RT) Cp c,+R 迈耶公式 dT R物理意义:1kg理想气体定压吸热过程中,温度升高1 度所作的体积膨胀功 k 令:比热比k=C,/Cv R 0 k-1 二理想气体内能和焓的确定
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 一.理想气体内能和焓的特性 理想气体比热容特性 c R dT d u RT dT dh c p = v + + = = ( ) c p − cv = R ——迈耶公式 R物理意义:1kg理想气体定压吸热过程中,温度升高1 度所作的体积膨胀功。 令:比热比k=cp/cv, R k k c p −1 = R k cv 1 1 − = 二.理想气体内能和焓的确定

第了章理想气体性质与过程 P7884 3-3理想气体的内能、焓和比热容 二理想气体内能和焓的确定 △M=2-41=42p-41=2m-41 Au=∫c,n △h=h2-h=2v-41=2p-41 h=∫c,d0 Py=RT 理想气体性质 uu(T),hh(T) Cp -cy=R
第3章 理想气体性质与过程 P78~84 3-3 理想气体的内能、焓和比热容 理想气体性质 二.理想气体内能和焓的确定 v p 1 2 2p 2v 2 1 2 1 2 1 u u u u u u u ∆ = − = p − = v − ∫ ∆u = cvdT 2 1 2 1 2 1 h h h u u u u ∆ = − = v − = p − ∫ ∆h = c pdT pv = RT u = u(T), h = h(T) c p − cv = R