
(2)堆积密度(表观密度):单位体积床层所具有的质量,即 A元 颗粒床层的特性 空隙率ε:单位体积床层所具有的空隙体积,即 一g-6 -0.47-0.70 2.比表面积:单位体积床层所具有的颗粒表面积,即 「巧, ,1g之心 4=产=空么-么+rg 5g)方=0-)a -(3-7) 1。 或 gy8互8_5S=a=a-a a万可7工7m7”R 所以 Pa=(1-)p -(3-8) 3.方向性 厂各向同性:床层截面上的空隙面积与床层截面积之比等于ε。 乙各向异性:出现壁效应,即壁面附近的空隙率较大,生产壁流
(2)堆积密度(表观密度):单位体积床层所具有的质量,即 三、颗粒床层的特性 1.空隙率:单位体积床层所具有的空隙体积,即 2. 比表面积ab:单位体积床层所具有的颗粒表面积,即 -(3-7) 或 所以 -(3-8) 3.方向性 各向同性:床层截面上的空隙面积与床层截面积之比等于。 各向异性:出现壁效应,即壁面附近的空隙率较大,生产壁流

第二节重力沉降 沉降速度 球形颗粒的自由沉降(单个颗粒沉降) 设某个球形颗粒在流体中自由沉降,则该颗粒所受力有: F:-5d'p8-mg 6 浮力 R=匹dpg 6 阻力 9=64 2 由牛顿第一定律( R=a,得 当 du de =0,解得 Ad(p,-p)g := 一沉降速度 35p 2.阻力系数g 通过量钢分析并结合实验测试,得出 5=fRe,鸟) 式中 Re,=dusp
第二节 重力沉降 一、沉降速度 1.球形颗粒的自由沉降(单个颗粒沉降) 设某个球形颗粒在流体中自由沉降,则该颗粒所受力有: 重力 浮力 阻力 由牛顿第二定律( ),得 当 时 ,解得 -沉降速度 2. 阻力系数 通过量钢分析并结合实验测试,得出 式中
对球形颗粒(s=1)的曲线,可按R分为三个区,各区的曲线可用相应的经验关联式表达: 24 Ret 层流区或Stokes定律区(104<Re,<1) 18.5 Re: 过渡流区或Allen定律区(1<Re<10) U.44, 湍流区或Newton:定律区(103<Re<2×105) 所以 d'(p,-p)g 层流区 18μ 过渡流区 4:=0.27 d(p,-p)g Re6 16 11 4:=0.154× d(e-p)g 0.406 DI UI 湍流区 4,=1.74 ld(p,-p)g 3.影响沉降速度的因素 (1)颗粒的体积浓度 浓度较高时,便发生干扰沉降 (2)器壁效应 当容器直径较小时,便发生受阻沉降 在Stokes?定律区,可按下式修正: 1+21月
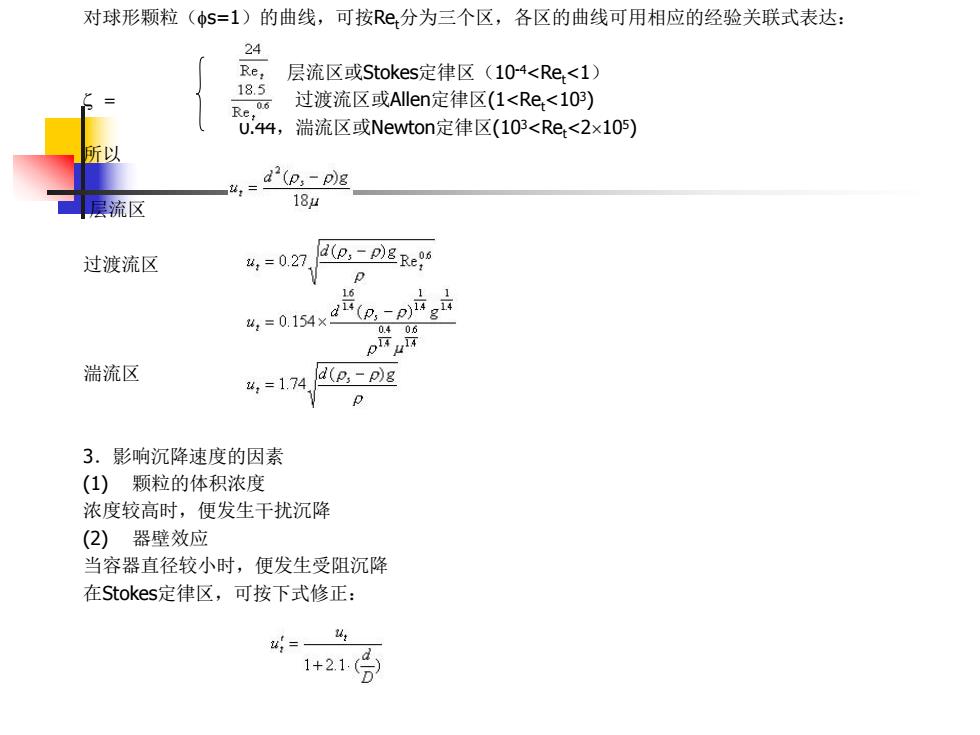
对球形颗粒(s=1)的曲线,可按Ret分为三个区,各区的曲线可用相应的经验关联式表达: 层流区或Stokes定律区(10-4<Ret<1) 过渡流区或Allen定律区(1<Ret<103) 0.44,湍流区或Newton定律区(103<Ret<2105) 所以 层流区 过渡流区 湍流区 3.影响沉降速度的因素 (1) 颗粒的体积浓度 浓度较高时,便发生干扰沉降 (2) 器壁效应 当容器直径较小时,便发生受阻沉降 在Stokes定律区,可按下式修正:

(3)颗粒形状 对非球形颗粒,其沉降得慢一些。修正如下: 图3-2 d。= →Reg 4. 沉降速度的计算 (1)试差法 假设沉降属于某一流型,则按该流型选择相应的公式计算u:再算Re校核流型。 流型→Ut→Re→流型→再设流型→. (2)摩擦数群法 由 ,= Ad(p,-p)g 得 5=4d(e.-p)8 3a4 而 Reg=diup 相乘得 5 Reo-DE(-du 3μ2 3 304, 由 =f(Re:) 知 5Re=p(Re)
(3) 颗粒形状 对非球形颗粒,其沉降得慢一些。修正如下: 图3-2 4.沉降速度的计算 (1) 试差法 假设沉降属于某一流型,则按该流型选择相应的公式计算ut;再算Ret校核流型。 流型 ut Ret 流型 再设流型 (2)摩擦数群法 由 得 而 相乘得 由 知

作图3-3:任取一4→ →5Re 计算: 5Re:B=3Re,→4, 求颗粒直径也可用类似的方法: 5Au(p,-p)8 4d(p,-p)g u 际得 Re: 3p'u 3pu?du,p 同理 =w®e,) Re, 作图3-3:任取一d→ Re,s色p 2→6→ e, 计算: 5=3→Re1→d Re; 此外,也可用无因次数群K值判别流型: 4,= d2(p,-p)g 将 184 代入Re,e 得 Re;= d'p(e,-0)K 18u 18 当 Re=1时,K=2.62 同理将 41=1.74 d(p,-p)g 代入Re,-P
作图3-3:任取一ut 计算: 求颗粒直径也可用类似的方法: 相除得 同理 作图3-3:任取一d 计算: 此外,也可用无因次数群K值判别流型: 将 代入 得 当 Ret=1 时,K=2.62 同理将 代入