算法总体思想 ■ 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 n12 n/2 n/2 n/2 T4)TA4)T64T(64)TA4)T(64)T(4)TA4T(4)T4) T64) 6
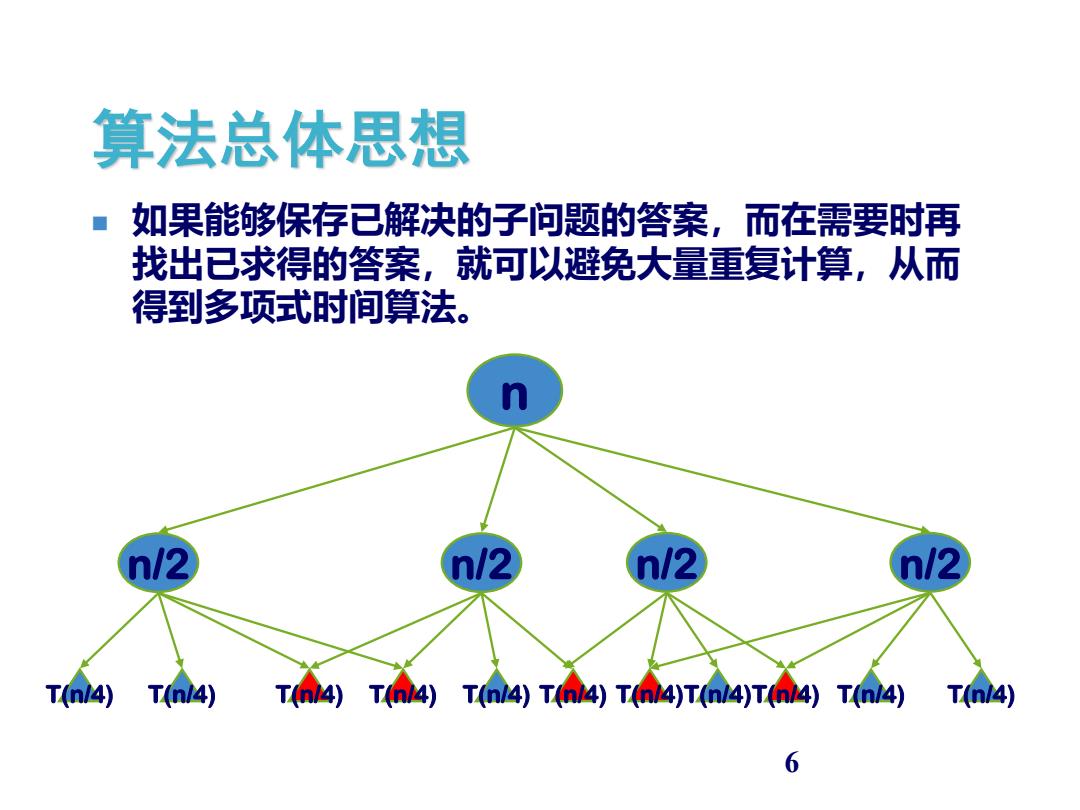
6 ◼ 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 算法总体思想 n n/2 T(n/4) T(n/4) T(n/4) T(n/4) n/2 n/2 T(n/4)T(n/4) n/2 T(n/4) T(n/4) T(n/4) T(n/4) T(n/4)

动态规划算法 CR 算法总体思想 动态规划算法与分治法类似,其基本思想也是将待求解问题 分解成若干个子问题 ⊕ 与分治法的区别在于 适用于动态规划算法求解的问题,经分解得到的子问题往 往不是互相独立的;若用分治法求解,则分解得到的子问 题数目太多,导致最终解决原问题需指数时间, 原因在于:虽然子问题的数目常常只有多项式量级,但在 用分治法求解时,有些子问题被重复计算了许多次 ⊕ 如果可以保存已解决的子问题的答案,就可以避免大量重复 计算,从而得到多项式时间的算法 动态规划法的基本思路是:构造一张表来记录所有已解决的 子问题的答案(无论算法形式如何,其填表格式是相同的)
动态规划算法 算法总体思想 动态规划算法与分治法类似,其基本思想也是将待求解问题 分解成若干个子问题 与分治法的区别在于 ━ 适用于动态规划算法求解的问题,经分解得到的子问题往 往不是互相独立的;若用分治法求解,则分解得到的子问 题数目太多,导致最终解决原问题需指数时间, ━ 原因在于:虽然子问题的数目常常只有多项式量级,但在 用分治法求解时,有些子问题被重复计算了许多次 如果可以保存已解决的子问题的答案,就可以避免大量重复 计算,从而得到多项式时间的算法 动态规划法的基本思路是:构造一张表来记录所有已解决的 子问题的答案(无论算法形式如何,其填表格式是相同的)

动态规划算法的基本步骤 1。找出最优解的性质(分析其结构特征) 2.递归地定义最优值(优化目标函数) 3.以自底向上的方式计算出最优值 4.根据计算最优值时得到的信息,构造最优解
动态规划算法的基本步骤 1. 找出最优解的性质(分析其结构特征) 2. 递归地定义最优值(优化目标函数) 3. 以自底向上的方式计算出最优值 4. 根据计算最优值时得到的信息,构造最优解

3.1矩阵连乘问题 (Matrix-Chain Multiplication)
3.1 矩阵连乘问题 (Matrix-Chain Multiplication)

两个矩阵相乘:标准解法 void matrixMultiply(int **Ma,int **Mb,int **Mc, int ra,int ca,int rb,int cb){ if(caI=rb)error("矩阵不可乘"): for (int i=0;i<ra;i++) for (int j=0;j<cb;j++){ int sum=a[i][o]*b[o][j]; for (int k=1;k<ca;k++) sum +a[i][k]*b[k][j]; } c[i][j]=sum; } } 设A是pXq的矩阵,B是qXr的矩阵,数乘次数为pxqxr 算法的时间复杂度为:O(n3)
两个矩阵相乘:标准解法 • 设A是pⅹq的矩阵,B是qⅹr的矩阵,数乘次数为pⅹqⅹr • 算法的时间复杂度为:O(n3) void matrixMultiply( int **Ma, int **Mb, int **Mc, int ra, int ca, int rb, int cb ) { if (ca != rb) error(“矩阵不可乘”); for (int i=0; i<ra; i++){ for (int j=0; j<cb; j++) { int sum=a[i][0]*b[0][j]; for (int k=1; k<ca; k++){ sum += a[i][k]*b[k][j]; } c[i][j]=sum; } } }