
Copyright by Dr.Zheyan Jin Chapter 3 Fundamentals of Inviscid,Incompressible Flow 3.4 Uniform Flow Consider a uniform flow with velocity Voriented in the positive x direction. 06=u=V. 80 =y=0 Ox dy w=const Integrate the above equation with respect to x,we have ='x+f(y) where f(y)is a function of y only Integrate the above equation with respect to y,we have 中=const+g(x) where g(x)is a function of x only Since is the same function. =Vx+const
Copyright by Dr. Zheyan Jin Chapter 3 Fundamentals of Chapter 3 Fundamentals of Inviscid Inviscid, Incompressible Flow , Incompressible Flow 3.4 Uniform Flow Integrate the above equation with respect to x, we have Since Φ is the same function. Consider a uniform flow with velocity V ͚oriented in the positive x direction. V x const V x f ( y ) 0 v y u V x where f(y) is a function of y only Integrate the above equation with respect to y, we have const g ( x ) where g(x) is a function of x only V͚ x y Φ=const ψ=const

Copyright by Dr.Zheyan Jin Chapter 3 Fundamentals of Inviscid,Incompressible Flow 3.4 Uniform Flow Note that in a practical aerodynamic problem, the actual value of is not significant; 8 rather,is always used to obtain the e velocity by differentiation;that is V=7中 w=const The velocity potential for a uniform flow with velocity Voriented in the positive x direction. φ=Vx Now,consider the incompressible steam function u a业=u=V. 0 dy O 2=-v=0 The stream function for a uniform flow with velocity V oriented in the positive x direction. ='y
Copyright by Dr. Zheyan Jin Chapter 3 Fundamentals of Chapter 3 Fundamentals of Inviscid Inviscid, Incompressible Flow , Incompressible Flow 3.4 Uniform Flow The velocity potential for a uniform flow with velocity V ͚oriented in the positive x direction. The stream function for a uniform flow with velocity V ͚oriented in the positive x direction. Note that in a practical aerodynamic problem, the actual value of Φ is not significant; rather, Φ is always used to obtain the velocity by differentiation; that is y V V x Now, consider the incompressible steam function ψ V͚ x y Φ=const ψ=const V 0 y x u V v

Copyright by Dr.Zheyan Jin Chapter 3 Fundamentals of Inviscid,Incompressible Flow 3.4 Uniform Flow b7。ds Circulation =-。·bds w=const T=/。。0=0 The result is consistent r=-x八as or V×7=0 (The uniform flow is irrotational) T=0 Conclusion:Circulation around any closed curve in a uniform flow is zero
Copyright by Dr. Zheyan Jin Chapter 3 Fundamentals of Chapter 3 Fundamentals of Inviscid Inviscid, Incompressible Flow , Incompressible Flow 3.4 Uniform Flow The result is consistent Circulation V͚ x y Φ=const ψ=const 0 0 C C V V d s V d s Conclusion: Circulation around any closed curve in a uniform flow is zero 0 0 S V V dS (The uniform flow is irrotational) or
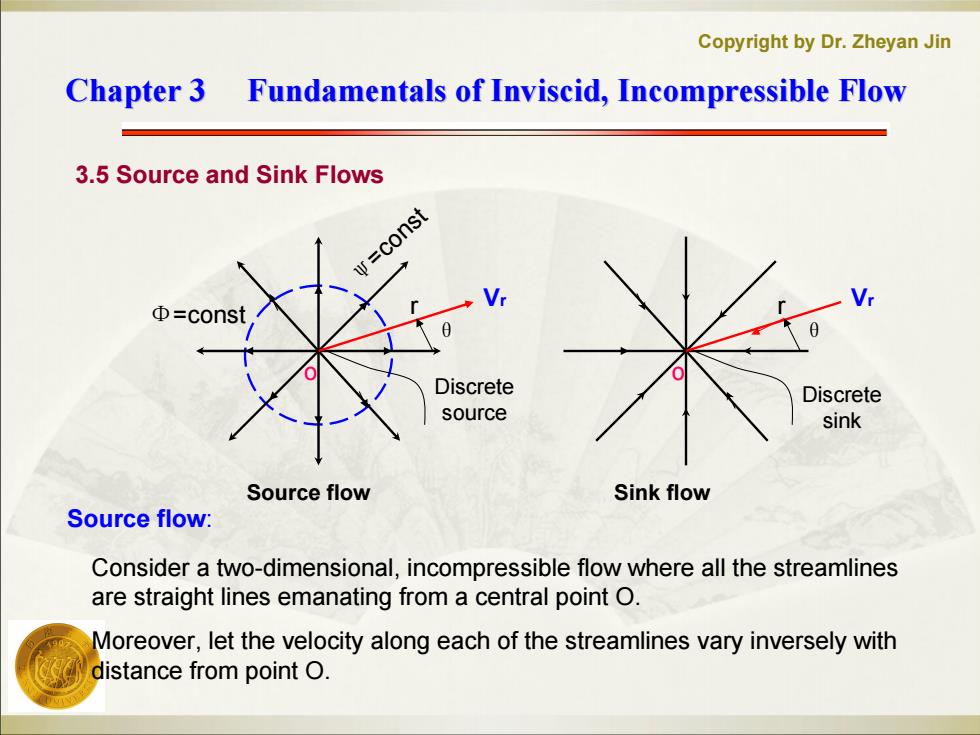
Copyright by Dr.Zheyan Jin Chapter 3 Fundamentals of Inviscid,Incompressible Flow 3.5 Source and Sink Flows w=const Φ=const Discrete Discrete source sink Source flow Sink flow Source flow: Consider a two-dimensional,incompressible flow where all the streamlines are straight lines emanating from a central point O. Moreover,let the velocity along each of the streamlines vary inversely with distance from point O
Copyright by Dr. Zheyan Jin Chapter 3 Fundamentals of Chapter 3 Fundamentals of Inviscid Inviscid, Incompressible Flow , Incompressible Flow 3.5 Source and Sink Flows Consider a two-dimensional, incompressible flow where all the streamlines are straight lines emanating from a central point O. Moreover, let the velocity along each of the streamlines vary inversely with distance from point O. Source flow: Source flow Vr θ Φ=const o r ψ=const Discrete source Sink flow Vr θ o r Discrete sink
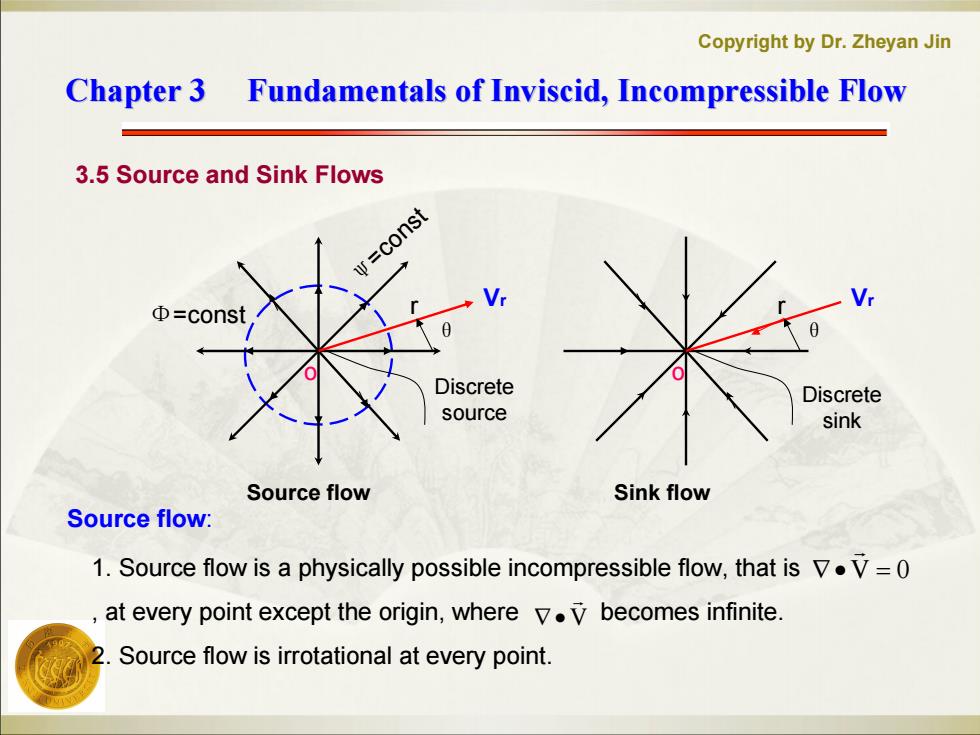
Copyright by Dr.Zheyan Jin Chapter 3 Fundamentals of Inviscid,Incompressible Flow 3.5 Source and Sink Flows =const Φ=const Discrete Discrete source sink Source flow Sink flow Source flow: 1.Source flow is a physically possible incompressible flow,that is V.V=0 at every point except the origin,where v.V becomes infinite. Source flow is irrotational at every point
Copyright by Dr. Zheyan Jin Chapter 3 Fundamentals of Chapter 3 Fundamentals of Inviscid Inviscid, Incompressible Flow , Incompressible Flow 3.5 Source and Sink Flows 1. Source flow is a physically possible incompressible flow, that is , at every point except the origin, where becomes infinite. 2. Source flow is irrotational at every point. Source flow: Source flow Vr θ Φ=const o r ψ=const Discrete source Sink flow Vr θ o r Discrete sink V 0V