智能系统：小型无人机纵向姿态模糊自适应PID控制与仿真

第3卷第2期 智能系统学报 Vol.3 Na 2 2008年4月 CAAI Transactions on Intelligent Systems Apr.2008 小型无人机纵向姿态模糊自适应PD控制与仿真 秦世引，陈锋，张永飞 (北京航空航天大学自动化科学与电气工程学院，北京100083) 摘要：针对某小型实验无人机智能自主飞行的要求，提出了一种无人机纵向姿态的模糊控制方法，设计了模糊自 适应PD控制器，可有效实现该无人机的纵向姿态控制和纵向航迹跟踪.仿真结果表明，所设计的模糊自适应PD 控制器较传统的PD控制器具有更好的控制性能，其响应快、超调小、精度高，而且鲁棒性和自适应能力也较强，可 满足自主飞行的要求」 关键词：自主飞行；模糊自适应PD;纵向姿态控制 中图分类号：TP273.1文献标识码：A文章编号：16734785(2008)02-0121-08 A fuzzy ada ptive PID controller for longitudinal attitude control of a small UaV QIN Shi-yin,CHEN Feng,ZHANG Yong-fei (School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China) Abstract:A fuzzy adaptive PID controller was developed for longitudinal attitude control of a small un- manned aerial vehicle (UAV).The proposed controller effectively implements longitudinal attitude and trajectory tracking control.Simulation results showed that the proposed fuzzy logic controller provides quicker response,smaller overshoot,higher precision,better robustness,and better adaptive ability than traditional PID controllers.It better satisfies the needs of autonomous flight. Keywords :autonomous flight:fuzzy adaptive PID:longitudinal attitude control 无人机完成自主飞行山，需要控制系统对内回性.其次，设计中使用的性能参数并不能真正体现飞 路（姿态回路）和外回路（水平位置和高度回路）都具机的实际性能，随着飞机状态的改变，所设计好的性 有良好的控制特性.内回路控制性能是外回路控制 能参数可能不能满足系统的要求.随后发展起来了一 的基础，其性能优劣直接影响外回路的控制结果，从种叫做非线性动态逆控制方法.该方法首先需要得到 而影响无人机自主飞行性能.典型的无人机内回路 非线性系统的逆模型，然后将逆模型作用到原系统 依靠飞行控制系统分别对纵向、横向和航向3个通 使系统的状态/控制输入从非线性系统通过局部微分 道进行协调控制，实现自动飞行.在纵向、横向和航 同胚一一映射到线性系统，将非线性问题转化为线性 向通道中，纵向通道控制律的设计最为关键且复杂， 控制问题该方法在理论、仿真及试飞中都得到了验 其控制效果将直接影响无人机的飞行性能 证和证明，己成功应用在现实中)，但是，该方法也存 传统的飞行控制系统设计，包括经典PD、线性 在局限性：它需要构造可信度高的非线性仿真模型并 二次校正器理论、模型跟踪、特征结构配置等，虽然在 通过机载计算机进行实时逆变换，计算量大，且不易 现实中有许多成功的应用，但也存在明显的缺点)， 进行鲁棒性分析等等.因此，针对上述这些方法的不 首先，设计中使用的是系统的线性化模型，这是一种 足，以及无人机模型的非线性时变特性，需寻求更加 近似模型，它忽略了飞机模型的不确定性和未建模特 智能的控制策略和方法。 模糊控制不需要获知系统的精确的数学模型， 收稿日期：2007-07-23. 它是以操作人员的经验为基础，根据操作者经验的 基金项目：国防基础科研基金资助项目(D2120060013);国家自然科 学基金重点资助项目(60736025) 语言表达来确定各个参数和控制规律，然后在实际 通讯作者：陈锋.E-mail:chenfeng0151002@163.com 系统中进行调试和整定，实践证明，模糊控制适用于 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

第 3 卷第 2 期 智 能 系 统 学 报 Vol. 3 №. 2 2008 年 4 月 CAA I Transactions on Intelligent Systems Apr. 2008 小型无人机纵向姿态模糊自适应 PID 控制与仿真 秦世引 , 陈 锋 , 张永飞 (北京航空航天大学 自动化科学与电气工程学院 , 北京 100083) 摘 要 :针对某小型实验无人机智能自主飞行的要求 ,提出了一种无人机纵向姿态的模糊控制方法 ,设计了模糊自 适应 PID 控制器 ,可有效实现该无人机的纵向姿态控制和纵向航迹跟踪. 仿真结果表明 ,所设计的模糊自适应 PID 控制器较传统的 PID 控制器具有更好的控制性能 ,其响应快、超调小、精度高 ,而且鲁棒性和自适应能力也较强 ,可 满足自主飞行的要求. 关键词 :自主飞行 ; 模糊自适应 PID ; 纵向姿态控制 中图分类号 : TP273. 1 文献标识码 :A 文章编号 :167324785 (2008) 0220121208 A fuzzy adaptive PID controller for longitudinal attitude control of a small UAV QIN Shi2yin , CH EN Feng , ZHAN G Yong2fei (School of Automation Science and Electrical Engineering , Beihang University , Beijing 100083 , China) Abstract :A f uzzy adaptive PID controller was developed for longit udinal attit ude control of a small un2 manned aerial vehicle ( UAV) . The proposed controller effectively implements longit udinal attit ude and trajectory tracking control. Simulation results showed that t he proposed f uzzy logic controller provides quicker response , smaller overshoot , higher precision , better robustness , and better adaptive ability than traditional PID controllers. It better satisfies t he needs of autonomous flight. Keywords :autonomous flight ; f uzzy adaptive PID ; longit udinal attit ude control 收稿日期 :2007207223. 基金项目 :国防基础科研基金资助项目(D2120060013) ;国家自然科 学基金重点资助项目(60736025) . 通讯作者 :陈 锋. E2mail :chenfeng0151002 @163. com. 无人机完成自主飞行[1 ] ,需要控制系统对内回 路(姿态回路) 和外回路(水平位置和高度回路) 都具 有良好的控制特性. 内回路控制性能是外回路控制 的基础 ,其性能优劣直接影响外回路的控制结果 ,从 而影响无人机自主飞行性能. 典型的无人机内回路 依靠飞行控制系统分别对纵向、横向和航向 3 个通 道进行协调控制 ,实现自动飞行. 在纵向、横向和航 向通道中 ,纵向通道控制律的设计最为关键且复杂 , 其控制效果将直接影响无人机的飞行性能. 传统的飞行控制系统设计 ,包括经典 PID、线性 二次校正器理论、模型跟踪、特征结构配置等 ,虽然在 现实中有许多成功的应用 ,但也存在明显的缺点[2 ] , 首先 ,设计中使用的是系统的线性化模型 ,这是一种 近似模型 ,它忽略了飞机模型的不确定性和未建模特 性.其次 ,设计中使用的性能参数并不能真正体现飞 机的实际性能 ,随着飞机状态的改变 ,所设计好的性 能参数可能不能满足系统的要求. 随后发展起来了一 种叫做非线性动态逆控制方法. 该方法首先需要得到 非线性系统的逆模型 ,然后将逆模型作用到原系统 , 使系统的状态/ 控制输入从非线性系统通过局部微分 同胚一一映射到线性系统 ,将非线性问题转化为线性 控制问题. 该方法在理论、仿真及试飞中都得到了验 证和证明 ,已成功应用在现实中[2 ] . 但是 ,该方法也存 在局限性:它需要构造可信度高的非线性仿真模型并 通过机载计算机进行实时逆变换 ,计算量大 ,且不易 进行鲁棒性分析等等. 因此 ,针对上述这些方法的不 足 ,以及无人机模型的非线性、时变特性 ,需寻求更加 智能的控制策略和方法. 模糊控制不需要获知系统的精确的数学模型 , 它是以操作人员的经验为基础 ,根据操作者经验的 语言表达来确定各个参数和控制规律 ,然后在实际 系统中进行调试和整定. 实践证明 ,模糊控制适用于

·122· 智能系统学报 第3卷 被控参量无精确的表达方法和被控制对象各种参数 do 之间的相互关系难以精确描述的情况.因此，本文针 dt rsin Y+gcos Y. 对一种小型实验无人机的纵向姿态控制和高度跟踪 dY p-tan s(rcos r-q sin ) (1 问题，设计了一种模糊自适应PD控制器，仿真结 果表明，其性能优于常规的PD控制器 表1无人机参数符号说明 1无人机的纵向姿态模型 Table 1 List of parameter symbols for UAV 参数名称 符号 参数名称 符号 本文中采用的小型实验无人机对象的实物如 无人机速度 滚转角速度 图1所示 D 无人机质量 俯仰角速度 发动机推力 偏航角速度 飞行阻力 D 滚转力矩 M 飞行升力 俯仰力矩 M: 侧力 偏航力矩 迎角 X轴转动惯量 侧滑角 Y轴转动惯量 图1小型实验无人机实物 俯仰角 Z轴转动惯量 Fig 1 Profile of the SUAV 偏航角 X轴距离 根据经典飞行控制理论，可建立小型无人机的 滚转角 y轴距离 Ya 12阶微分方程模型，其中包括动力学模型和运动学 模型1，如式(1)所示.其中，各符号与变量/参数的 航迹角 Z轴距离 Z 对应关系见表1 航迹偏转角 翼展 b mos)csBD.mgsin 速度滚转角 方 机翼面积 my do 升降舵 动压 =T[cos(a+中sin Bsin+ 副翼舵 6 平均气动弦长 sin (a+r)cos Y1+Lcos Y- Zsin⅓-mgcos8, 利用水平无侧滑飞行条件Y=B司和p=r= ~mVcos od边 0,将飞机运动方程解耦为不依赖于横侧向状态量 dt TI-cos(a+r)sin os (B,Y,p,r,吻的纵向运动方程： sin(a+r)sin ]Lsin Zcos ml Tcos a-D-mgsin 0. d=Vcos0cos攻， mVo Tsin a +L-mgcos 0. d 2) a=q-0, dya =y sin 0. dr I:g =M:. 式中：T、D、L及M:分别为发动机推力、气流阻力、 =-Vcos0sin克， dt 升力及绕俯仰轴力矩，这些参量的确定需要根据飞 机当前的飞行状态实时地确定，在此以飞机某一平 1,=M-(h.-gr di 衡状态为基准运动，小扰动情况下假设这些力和力 b出=Mhpg 矩为相应量的线性关系， 若将无人机的定常直线无侧滑飞行作为基准运 品=Mdpr 动，在小扰动假设下就可得到无人机的纵向近似模 型为 sn 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

被控参量无精确的表达方法和被控制对象各种参数 之间的相互关系难以精确描述的情况. 因此 ,本文针 对一种小型实验无人机的纵向姿态控制和高度跟踪 问题 ,设计了一种模糊自适应 PID 控制器 ,仿真结 果表明 ,其性能优于常规的 PID 控制器. 1 无人机的纵向姿态模型 本文中采用的小型实验无人机对象的实物如 图 1 所示. 图 1 小型实验无人机实物 Fig11 Profile of the SUAV 根据经典飞行控制理论 ,可建立小型无人机的 12 阶微分方程模型 ,其中包括动力学模型和运动学 模型[ 3 ] ,如式 (1) 所示. 其中 ,各符号与变量/ 参数的 对应关系见表 1. m dV dt = Tcos(α+φT ) cosβ- D - mg sinθ, mV dθ dt = T[cos (α+φT ) sinβsinγs + sin (α+φT ) cosγs ] + Lcosγs - Zsinγs - mgcosθ, - mV cosθdψs dt = T[ - cos(α+φT ) sinβcosγs + sin (α+φT ) sinγs ] + L sinγs + Zcosγs , d x d dt = V co sθcosψs , d y d dt = V sinθ, dz d dt = - V cosθsinψs , I x d p dt = Mx - ( Iz - I y ) q ·r, I y d r dt = My - ( I x - Iz ) p ·q , Iz dq dt = Mz - ( I y - I x ) p ·r, dψ dt = 1 cos ; ( rcosγ- qsinγ) , d; dt = rsinγ+ q cosγ, dγ dt = p - tan ; ( rcosγ- q sinγ) . (1) 表 1 无人机参数符号说明 Table 1 List of parameter symbols for UAV 参数名称 符号 参数名称 符号 无人机速度 V 滚转角速度 p 无人机质量 m 俯仰角速度 q 发动机推力 T 偏航角速度 r 飞行阻力 D 滚转力矩 Mx 飞行升力 L 俯仰力矩 Mz 侧力 Z 偏航力矩 My 迎角 α X 轴转动惯量 I x 侧滑角 β Y 轴转动惯量 I y 俯仰角 ; Z 轴转动惯量 Iz 偏航角 ψ X 轴距离 X d 滚转角 γ Y 轴距离 Y d 航迹角 θ Z 轴距离 Zd 航迹偏转角 ψs 翼展 b 速度滚转角 γs 机翼面积 S 升降舵 δe 动压 …q 副翼舵 δa 平均气动弦长 €c 利用水平无侧滑飞行条件γ=β≡0 和 p = r ≡ 0 ,将飞机运动方程解耦为不依赖于横侧向状态量 (β,γ, p , r,ψ) 的纵向运动方程 : mVÛ= Tcosα- D - mg sinθ, mVθÛ= Tsinα+ L - mgcosθ, αÛ= q - θÛ, IzÛq = Mz . (2) 式中 : T、D、L 及 M z 分别为发动机推力、气流阻力、 升力及绕俯仰轴力矩 ,这些参量的确定需要根据飞 机当前的飞行状态实时地确定 ,在此以飞机某一平 衡状态为基准运动 ,小扰动情况下假设这些力和力 矩为相应量的线性关系. 若将无人机的定常直线无侧滑飞行作为基准运 动 ,在小扰动假设下就可得到无人机的纵向近似模 型为 · 221 · 智 能 系 统 学 报 第 3 卷

第2期 秦世引，等：小型无人机纵向姿态模糊自适应PD控制与仿真 ·123· mP=(0+ OTAv+ Cy 8)cos a-(Do+ 规则进行推理控制，而不依赖于被控对象精确的数 a6. 学模型.但是存在一个严重的缺点就是它对语言 aDAv+ aDAa+ 2D6).mg sin 0. 变量值的划分不可能太细，导致对系统的控制精度 Cy da do. 有一定的影响.由于实际中多采用二维的模糊控制， mV0 Tsin a+(Lo Ov OLAa+ a 模糊控制器的输出一般与误差及误差的变化有关 △d+△g+80).mgos0 因此这种控制器只具有Fuzy比例微分控制作 da 08 用，若模糊控制中不引入积分机制，从理论上来讲这 à=q-0, 种常规的模糊控制器是很难克服稳态误差的.但是 1.g-Mo+Aad+ 传统PD控制器具有积分环节，能很好地消除稳态 dy da da 误差，如果将模糊决策方法与PD控制相融合，那 5 M-Aq+08. 么控制器既具有模糊控制的特点又具有PD的特 点.在整定好一组PD控制参数后，采用模糊自适 本文中，该小型无人机质量m=9kg,气动弦长 应PD控制器比常规模糊控制器能更好更快的满 c=0.28m,机翼展长b=2.8m,飞行推理T= 足系统要求，它既具有模糊控制器的优点，又具有常 15N,飞机的气动导数可以通过吹风试验并进行计 规PD控制器的优点，因此本文也采用了这种方法 算得到.在平飞条件下飞行速度V。=20m/s,迎角 来控制无人机姿态 4=2.68/57.3rad,高度H=200m.根据试验数 模糊自适应PD控制器I68]以误差e和误差变 据进行一阶近似简化后，可得在平飞条件下的纵向 化率ec作为输入，利用模糊控制规则在线对PD参 平面小扰动近似模型为 数进行修改，以满足不同时刻的e和e:对PD参数 p=0.4877-0.0151V)cosa- 自整定的要求.模糊自适应PD控制器结构]如 (-0.4424+0.0302V+0.4840a- 下图2所示」 gsin a). à=Vg-0.4877-0.0151)sina- 模糊 模糊化 (-15.7578+0.9800Ψ+127.4a+ 应参 模糊推理 模糊规则 规则史新 0.0172à+0.4040g+ 数整 知识库 3.1850+gc0s(8-4, 去模糊化 8=q, 俯仰角给 △k△△k 定值， 小型航空 俯仰角实际 9=2.2460-48.02a.5.7505g- PID 飞行器纵输出值8 55.73758-0.2401à， 控制器 态模 H=Vsin(-☑. (4) 从方程组(4)可以看出，该模型呈现非线性特 性，并且，模型中各参数的逼近只采用了一阶近似， 图2模糊自适应PD控制器结构 和其实际值之间还存在一个高阶偏差量，采用常规 Fig 2 Structure of fuzzy adaptive PID controller PD控制方法不容易进行控制器设计，并且由于模 模糊自适应PD控制器的参数模糊自整定是 型不准确，对于近似模型设计的最优PD控制器在 找出PD的3个参数变化量△Kp,△K,△Ko与误 实际控制中也未必是最优的；此外，由于飞机实际飞 差e和误差变化率e.之间的模糊关系，在运行中通 行环境复杂，可能导致模型参数的改变，而传统PD 过不断检测e和ec,根据模糊控制原理来对3个参 控制无法很好地应对这些改变.因此对于该模型，传 数进行在线修改，以满足不同e和ee时对控制参数 统PD控制无法取得很好的控制效果，应当寻求具 的要求，从而使被控对象有良好的动、静态性能 有自适应功能的智能化控制策略和方法， 2.2模糊P1D控制器的设计 2模糊自适应PD控制器的组织结 模糊控制器选用误差量e和误差的变化量e 作为输入变量，PD控制器的3个参数变化量△K,, 构和实现算法 △K,△Ko作为输出变量.对这5个变量对应的模糊 2.1模糊PD控制器结构及原理 语言集及其论域定义为 模糊控制是以专家的经验为基础，制定模糊 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

mVÛ= ( T0 + 5 T 5v Δv + 5 T 5δe δe ) cosα- ( D0 + 5D 5v Δv + 5D 5α Δα+ 5D 5δe δe ) - mg sinθ, mVθÛ= Tsinα+ ( L0 + 5L 5v Δv + 5L 5α Δα+ 5L 5αÛ ΔαÛ+ 5L 5q Δq + 5D 5δe δe ) - mg cosθ, αÛ= q - θÛ, IzÛq = Mz0 + 5Mz 5v Δv + 5Mz 5α Δα+ 5Mz 5αÛ ΔαÛ+ 5Mz 5q Δq + 5Mz 5δe δe . (3) 本文中 ,该小型无人机质量 m = 9 kg ,气动弦长 €c = 0128 m , 机翼展长 b = 218 m , 飞行推理 T = 15 N ,飞机的气动导数可以通过吹风试验并进行计 算得到. 在平飞条件下飞行速度 V 0 = 20 m/ s,迎角 α0 = 2168/ 5713 rad ,高度 H0 = 200 m. 根据试验数 据进行一阶近似简化后 ,可得在平飞条件下的纵向 平面小扰动近似模型为 VÛ= (0. 487 7 - 0. 015 1V ) co sα- ( - 0. 442 4 + 0. 030 2V + 0. 484 0α) - gsin ( ; - α) , VαÛ= V q - (0. 487 7 - 0. 015 1V ) sinα- ( - 15. 757 8 + 0. 980 0V + 127. 4α+ 0. 017 2αÛ+ 0. 404 0q + 3. 185 0δe ) + gcos( ; - α) , Û; = q , Ûq = 2. 246 0 - 48. 02α- 5. 750 5q - 55. 737 5δe - 0. 240 1αÛ, HÛ= V sin ( ; - α) . (4) 从方程组 (4) 可以看出 ,该模型呈现非线性特 性 ,并且 ,模型中各参数的逼近只采用了一阶近似 , 和其实际值之间还存在一个高阶偏差量 ,采用常规 PID 控制方法不容易进行控制器设计 ,并且由于模 型不准确 ,对于近似模型设计的最优 PID 控制器在 实际控制中也未必是最优的 ;此外 ,由于飞机实际飞 行环境复杂 ,可能导致模型参数的改变 ,而传统 PID 控制无法很好地应对这些改变. 因此对于该模型 ,传 统 PID 控制无法取得很好的控制效果 ,应当寻求具 有自适应功能的智能化控制策略和方法. 2 模糊自适应 PID 控制器的组织结 构和实现算法 211 模糊 PID 控制器结构及原理 模糊控制是以专家的经验为基础 ,制定模糊 规则进行推理控制 ,而不依赖于被控对象精确的数 学模型. 但是存在一个严重的缺点[4 ] 就是它对语言 变量值的划分不可能太细 ,导致对系统的控制精度 有一定的影响. 由于实际中多采用二维的模糊控制 , 模糊控制器的输出一般与误差及误差的变化有关 , 因此这种控制器只具有 Fuzzy 比例 —微分控制作 用 ,若模糊控制中不引入积分机制 ,从理论上来讲这 种常规的模糊控制器是很难克服稳态误差的. 但是 传统 PID 控制器具有积分环节 ,能很好地消除稳态 误差 ,如果将模糊决策方法与 PID 控制相融合 ,那 么控制器既具有模糊控制的特点又具有 PID 的特 点. 在整定好一组 PID 控制参数后 ,采用模糊自适 应 PID 控制器比常规模糊控制器能更好更快的满 足系统要求 ,它既具有模糊控制器的优点 ,又具有常 规 PID 控制器的优点 ,因此本文也采用了这种方法 来控制无人机姿态. 模糊自适应 PID 控制器[ 628 ] 以误差 e 和误差变 化率 ec 作为输入 ,利用模糊控制规则在线对 PID 参 数进行修改 ,以满足不同时刻的 e 和 ec 对 PID 参数 自整定的要求. 模糊自适应 PID 控制器结构[529 ] 如 下图 2 所示. 图 2 模糊自适应 PID 控制器结构 Fig12 Structure of fuzzy adaptive PID controller 模糊自适应 PID 控制器的参数模糊自整定是 找出 PID 的 3 个参数变化量ΔKP ,ΔKI ,ΔKD 与误 差 e 和误差变化率 ec 之间的模糊关系 ,在运行中通 过不断检测 e 和 ec ,根据模糊控制原理来对 3 个参 数进行在线修改 ,以满足不同 e 和 ec 时对控制参数 的要求 ,从而使被控对象有良好的动、静态性能. 212 模糊 PI D 控制器的设计 模糊控制器选用误差量 e 和误差的变化量 ec 作为输入变量 ,PID 控制器的 3 个参数变化量ΔKP , ΔKI ,ΔKD 作为输出变量. 对这 5 个变量对应的模糊 语言集及其论域定义为 第 2 期 秦世引 ,等 :小型无人机纵向姿态模糊自适应 PID 控制与仿真 · 321 ·

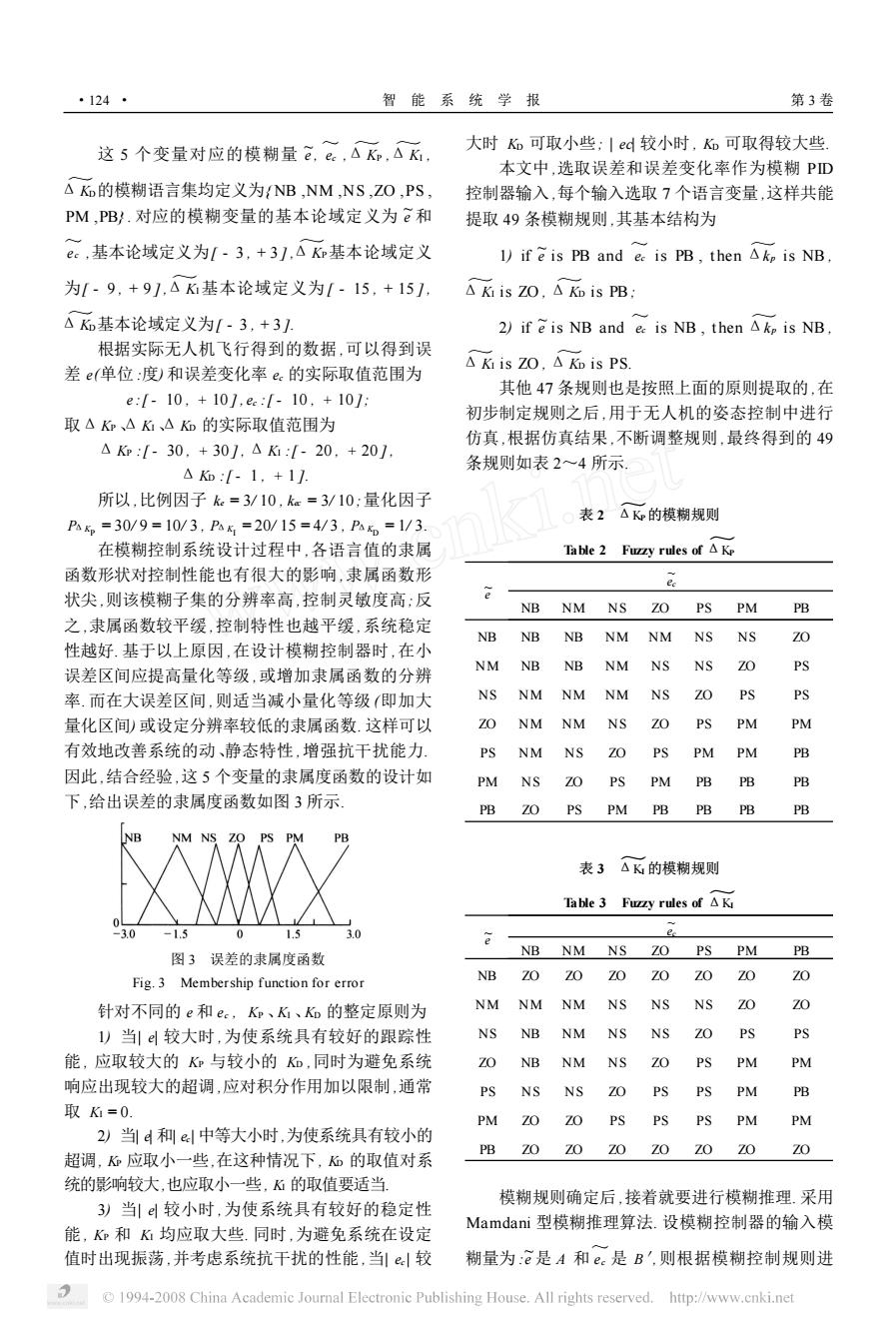
·124· 智能系统学报 第3卷 这5个变量对应的模糊量e,e,△k△k. 大时Ko可取小些；|ed较小时，o可取得较大些. 本文中，选取误差和误差变化率作为模糊PD △K的模糊语言集均定义为NB,NM,NS,ZO,PS, 控制器输入，每个输入选取7个语言变量，这样共能 PM,PB/.对应的模糊变量的基本论域定义为e和 提取49条模糊规则，其基本结构为 e:,基本论域定义为[-3，+3]，△m基本论域定义 1)if e is PB and ee is PB.then Akp is NB. 为[-9，+91，△K基本论域定义为[-15，+15]， △kisZ0,△isPB: △K基本论域定义为[-3，+3] 2)if eis NB and ee is NB,then Akp is NB. 根据实际无人机飞行得到的数据，可以得到误 差e(单位：度)和误差变化率e.的实际取值范围为 △kisZ0,△KD is PS. 其他47条规则也是按照上面的原则提取的，在 e:[-10,+101,ee:[-10,+10]: 初步制定规则之后，用于无人机的姿态控制中进行 取△K、△K、△的实际取值范围为 仿真，根据仿真结果，不断调整规则，最终得到的49 △K:-30,+30],△：[-20，+201 条规则如表2~4所示 △K:[-1,+11, 所以，比例因子k=3/10,ke=3/10:量化因子 表2 △K的模糊规则 Pp=30/9=10/3,Pk=20/15=4/3,P=1/3. 在模糊控制系统设计过程中，各语言值的隶属 Table2 Furzy rules of△Ke 函数形状对控制性能也有很大的影响，隶属函数形 ec 状尖，则该模糊子集的分辨率高，控制灵敏度高：反 NB Nm NS ZO PS PM PB 之，隶属函数较平缓，控制特性也越平缓，系统稳定 NB NB NB NM NM NSNS ZO 性越好.基于以上原因，在设计模糊控制器时，在小 NM NB Nb Nm NS NS ZO 误差区间应提高量化等级，或增加隶属函数的分辨 率.而在大误差区间，则适当减小量化等级即加大 NS NM NM NM NS ZO PS PS 量化区间)或设定分辨率较低的隶属函数.这样可以 NM NM NS PS PM PM 有效地改善系统的动、静态特性，增强抗干扰能力. PS NM NS ZO PS PM PM PB 因此，结合经验，这5个变量的隶属度函数的设计如 PM NS ZO PS PM PB PB PB 下，给出误差的隶属度函数如图3所示。 PB ZO PS PM PB PB PB PB NR NM NS 70 PS PB 表3 △K的模糊规则 Table3 Fuzzy rules of△K 3.0 -1.5 0 1.5 3.0 e NB NM NS ZO PS PM PB 图3误差的隶属度函数 Fig.3 Membership function for error NB ZO ZO 针对不同的e和ee,Kr、K、Ko的整定原则为 NMNM NM NS NS NS ZO ZO l)当|较大时，为使系统具有较好的跟踪性 NS NB NM NS NS PS PS 能，应取较大的K与较小的和，同时为避免系统 ZO NB NM NS ZO PS PM PM 响应出现较大的超调，应对积分作用加以限制，通常 PS NS NS ZO PS PS PM 型 取K=0. PM PS PS PS PM PM 2)当l4和中等大小时，为使系统具有较小的 PB ZO 超调，应取小一些，在这种情况下，而的取值对系 统的影响较大，也应取小一些，的取值要适当， 3)当|较小时，为使系统具有较好的稳定性 模糊规则确定后，接着就要进行模糊推理.采用 Mamdani型模糊推理算法.设模糊控制器的输入模 能，K和K均应取大些.同时，为避免系统在设定 值时出现振荡，并考虑系统抗干扰的性能，当|e较 糊量为：e是A和ec是B',则根据模糊控制规则进 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

这 5 个变量对应的模糊量 „e , ec ～,ΔKP ～ ,ΔKI ～, ΔKD ～的模糊语言集均定义为{ NB ,NM ,NS ,ZO ,PS , PM ,PB} . 对应的模糊变量的基本论域定义为 „e 和 ec ～ ,基本论域定义为[ - 3 , + 3 ] ,ΔKP ～基本论域定义 为[ - 9 , + 9 ] ,ΔKI ～基本论域定义为[ - 15 , + 15 ] , ΔKD ～基本论域定义为[ - 3 , + 3 ]. 根据实际无人机飞行得到的数据 ,可以得到误 差 e(单位 :度) 和误差变化率 ec 的实际取值范围为 e :[ - 10 , + 10 ] , ec :[ - 10 , + 10 ]; 取ΔKP 、ΔKI 、ΔKD 的实际取值范围为 ΔKP :[ - 30 , + 30 ] , ΔKI :[ - 20 , + 20 ] , ΔKD :[ - 1 , + 1 ]. 所以 ,比例因子 ke = 3/ 10 , kec = 3/ 10 ;量化因子 PΔKP = 30/ 9 = 10/ 3 , PΔKI = 20/ 15 = 4/ 3 , PΔKD = 1/ 3. 在模糊控制系统设计过程中 ,各语言值的隶属 函数形状对控制性能也有很大的影响 ,隶属函数形 状尖 ,则该模糊子集的分辨率高 ,控制灵敏度高;反 之 ,隶属函数较平缓 ,控制特性也越平缓 ,系统稳定 性越好. 基于以上原因 ,在设计模糊控制器时 ,在小 误差区间应提高量化等级 ,或增加隶属函数的分辨 率. 而在大误差区间 ,则适当减小量化等级 (即加大 量化区间) 或设定分辨率较低的隶属函数. 这样可以 有效地改善系统的动、静态特性 ,增强抗干扰能力. 因此 ,结合经验 ,这 5 个变量的隶属度函数的设计如 下 ,给出误差的隶属度函数如图 3 所示. 图 3 误差的隶属度函数 Fig. 3 Membership function for error 针对不同的 e 和 ec , KP 、KI 、KD 的整定原则为 1) 当| e| 较大时 ,为使系统具有较好的跟踪性 能 , 应取较大的 KP 与较小的 KD ,同时为避免系统 响应出现较大的超调 ,应对积分作用加以限制 ,通常 取 KI = 0. 2) 当| e| 和| ec | 中等大小时,为使系统具有较小的 超调, KP 应取小一些,在这种情况下, KD 的取值对系 统的影响较大,也应取小一些, KI 的取值要适当. 3) 当| e| 较小时 ,为使系统具有较好的稳定性 能 , KP 和 KI 均应取大些. 同时 ,为避免系统在设定 值时出现振荡 ,并考虑系统抗干扰的性能 ,当| ec | 较 大时 KD 可取小些; | ec| 较小时 , KD 可取得较大些. 本文中 ,选取误差和误差变化率作为模糊 PID 控制器输入 ,每个输入选取 7 个语言变量 ,这样共能 提取 49 条模糊规则 ,其基本结构为 1) if „e is PB and ec ～ is PB , t hen Δk p ～ is NB , ΔKI ～is ZO , ΔKD ～ is PB; 2) if „e is NB and ec ～ is NB , t hen Δk p ～is NB , ΔKI ～is ZO , ΔKD ～ is PS. 其他 47 条规则也是按照上面的原则提取的 ,在 初步制定规则之后 ,用于无人机的姿态控制中进行 仿真 ,根据仿真结果 ,不断调整规则 ,最终得到的 49 条规则如表 2～4 所示. 表 2 Δ ～KP的模糊规则 Table 2 Fuzzy rules of Δ ～KP „e ec ～ NB NM NS ZO PS PM PB NB NB NB NM NM NS NS ZO NM NB NB NM NS NS ZO PS NS NM NM NM NS ZO PS PS ZO NM NM NS ZO PS PM PM PS NM NS ZO PS PM PM PB PM NS ZO PS PM PB PB PB PB ZO PS PM PB PB PB PB 表 3 Δ ～KI 的模糊规则 Table 3 Fuzzy rules of Δ ～KI „e ec ～ NB NM NS ZO PS PM PB NB ZO ZO ZO ZO ZO ZO ZO NM NM NM NS NS NS ZO ZO NS NB NM NS NS ZO PS PS ZO NB NM NS ZO PS PM PM PS NS NS ZO PS PS PM PB PM ZO ZO PS PS PS PM PM PB ZO ZO ZO ZO ZO ZO ZO 模糊规则确定后 ,接着就要进行模糊推理. 采用 Mamdani 型模糊推理算法. 设模糊控制器的输入模 糊量为 :„e 是 A 和 ec ～是 B′,则根据模糊控制规则进 · 421 · 智 能 系 统 学 报 第 3 卷

第2期 秦世引，等：小型无人机纵向姿态模糊自适应PD控制与仿真 ·125· 行近似推理，可以得出输出模糊量（用模糊集合C K=k%+△KP 表示)为 K=k。+△K, 10) R=(A,and B)→C. K=k4+△K R=UR (5) 式中：△K,、△K、△Ko为模糊控制器输出的3个自 1-1 R=(A:andB)→C. 适应修正值，k,、k。、k品为己整定好的PD的3个 初始参数值 2.3稳定性分析 表4△ka的模糊规则 为了保证系统稳定，需要针对所设计的模糊自 Table4 Furzy rules of△ka 适应PD控制器，采用输入/输出(/O)稳定性理 论1进行分析」 Be NB NM Ns ZO PS PM PB 为讨论方便，在此采用线性近似法)对无人机 NB PS NS NB NB NB NM PS 模型进行简化，从而将其改写成单输入单输出的形 式，输入为升降舵偏转角6，输出为俯仰角偏转角， NM PS NS NB NM NM NS ZO 这样就可得到传递函数模型为 NS NS NM NM Ns NS ZO .557(+6271)(x+04526 ZO ZO NS NS NS NS NS ZO Gy=2+0.38615+0.2714y6+12.45s+84.34训 PS ZO ZO ZO ZO ZO ZO ZO 根据VO稳定性定理，只要分别证明传递函数 PM PB NS PS PS PM PM PB G(y和模糊PD控制器分别为钝性和严格钝性，就 PB PB PM PM PM PS PS PB 能导出系统稳定的充分条件： 由钝性定理可知，被控对象G(s)本身不是钝性 其中包括3种主要的模糊逻辑运算：and运算， 的，因此，参照文献10]，对被控对象和控制器分别 合成运算“0”，蕴含运算“→” 本文and运算采用求交（取小）方法： 乘以-仕n以和+pg+四由钝 凸a'adB3(x,以=L'(x)∧4g(x)= 性定理可知，当p、Pm满足一定的条件时，就能保证 被控对象是钝性的，在此，通过计算，选取p1=1, minf4'(x,a(x划J. 6) 合成运算“o”采用最大-最小(max-min com- P2=2.经变换后的模糊自适应PD控制器的等效 传递函数为 position)方法： e(以=，XIa'x,》Ah(x,y,] G9=+作+2+女+g () 由钝性定理可知，要使G·(s为严格钝的，需满 蕴含运算“→”采用求交取小)方法： 足ReGG叫)≥6，其中6>0.因而有， R:44,d℃，(x,y,2)= Re(G':(jo)Re/Kij++kojoy? 4a,and(x,以∧e,(= ·Gw+V60+2)1= Rel-1 Ko)ik minf4aand(x,以，此，(}. (8) 2.d+3 去模糊化采用重心法： Re1.LM:a±i4Pd341= 2-)2+9d SuHe(u) (Ki Kpai)2.a)+3Kpoi (9) 2-)2+9d P4( Kn a (3 Kp-Ki-2 Kpl ai+2Ki (11) 经过去模糊化后的输出值再乘以比例因子就是 2-d)2+9d 实际的用于控制的真实值 由式11)可知，要使Re(G:o)N+6≥6，必须 以上模糊规则的设计是基于己获得一整定好 使K<0,KD④，3K-K-2K. (但不是最优)的PD参数的基础之上的.因此，根 从而可知，本文针对小型无人机非线性被控对 据模糊规则表进行推理最终得到3个参数的自适应 象所设计的模糊自适应PD器，整体系统满足VO 修正值，修正参数按式(10)计算： 稳定的充分条件为 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net

行近似推理 ,可以得出输出模糊量 …u (用模糊集合 C′ 表示) 为 Ri = ( A i and Bi) →Ci , R = ∪ n i = 1 Ri , Ri = ( A i and Bi) →Ci . (5) 表 4 Δ ～kd 的模糊规则 Table 4 Fuzzy rules of Δ ～kd „e ec ～ NB NM NS ZO PS PM PB NB PS NS NB NB NB NM PS NM PS NS NB NM NM NS ZO NS ZO NS NM NM NS NS ZO ZO ZO NS NS NS NS NS ZO PS ZO ZO ZO ZO ZO ZO ZO PM PB NS PS PS PM PM PB PB PB PM PM PM PS PS PB 其中包括 3 种主要的模糊逻辑运算 :and 运算 , 合成运算“. ”,蕴含运算“→”. 本文 and 运算采用求交(取小) 方法 : μ( A′and B′) ( x , y) = μA′( x) ∧μB′( x) = min[μA′( x) ,μB′( x) ]. (6) 合成运算“. ”采用最大 - 最小(max - min com2 position) 方法 : μC′( z) = ∨x , y ∈X , Y [μ( A′and B′) ( x , y) ∧μR ( x , y , z) ]. (7) 蕴含运算“→”采用求交(取小) 方法 : Ri ∴μ( A i and B i ) →Ci ( x , y , z) = μ( A i and B i ) ( x , y) ∧μCi ( z) = min{μ( A i and B i ) ( x , y) ,μCi ( z) } . (8) 去模糊化采用重心法 : u0 = ∑ n i = 1 uμi C′( ui) ∑ n i = 1 μC′( ui) . (9) 经过去模糊化后的输出值再乘以比例因子就是 实际的用于控制的真实值. 以上模糊规则的设计是基于已获得一整定好 (但不是最优) 的 PID 参数的基础之上的. 因此 ,根 据模糊规则表进行推理最终得到 3 个参数的自适应 修正值 ,修正参数按式(10) 计算 : KP = k p 0 +ΔKP , KI = ki 0 +ΔKI , KD = k d 0 +ΔKD . (10) 式中 :ΔKP 、ΔKI 、ΔKD 为模糊控制器输出的 3 个自 适应修正值 , k p 0 、ki 0 、kd 0 为已整定好的 PID 的 3 个 初始参数值. 213 稳定性分析 为了保证系统稳定 ,需要针对所设计的模糊自 适应 PID 控制器 , 采用输入/ 输出 ( I/ O) 稳定性理 论[10 ]进行分析. 为讨论方便 ,在此采用线性近似法[11 ]对无人机 模型进行简化 ,从而将其改写成单输入单输出的形 式 ,输入为升降舵偏转角δ,输出为俯仰角偏转角 ; , 这样就可得到传递函数模型为 G(s) = - 55. 7 (s + 6. 271) (s + 0. 452 6) (s 2 + 0. 386 1s + 0. 271 4) (s 2 + 12. 45s + 84. 34) . 根据 I/ O 稳定性定理 ,只要分别证明传递函数 G(s) 和模糊 PID 控制器分别为钝性和严格钝性 ,就 能导出系统稳定的充分条件. 由钝性定理可知 ,被控对象 G(s) 本身不是钝性 的 ,因此 ,参照文献[10 ] ,对被控对象和控制器分别 乘以 - (s + p1 ) (s + p2 ) s 和 s - (s + p1 ) (s + p2 ) . 由钝 性定理可知 ,当 p1 、p2 满足一定的条件时 ,就能保证 被控对象是钝性的 , 在此 ,通过计算 , 选取 p1 = 1 , p2 = 2. 经变换后的模糊自适应 PID 控制器的等效 传递函数为 G′c (s) = s - (s + 1) (s + 2) ( KP + KI s + KD s) . 由钝性定理可知 ,要使 G′c (s) 为严格钝的 ,需满 足 Re ( G′c (jω) ) ≥δ,其中δ> 0. 因而有 , Re ( G′c (jω) ) = Re[ KP jω+ KI + KD (jω) 2 - (jω+ 1) (jω+ 2) ] = Re[ - ( KI - KDω2 ) + j KPω 2 - ω2 + 3ωj ] = Re[ - ( ( KI - KDω2 ) + j KPω) (2 - ω2 - 3ωj) (2 - ω2 ) 2 + 9ω2 ] = - ( KI - KDω2 ) (2 - ω2 ) + 3 KPω2 (2 - ω2 ) 2 + 9ω2 = - KDω4 + (3 KP - KI - 2 KD )ω2 + 2 KI (2 - ω2 ) 2 + 9ω2 (11) 由式(11) 可知 ,要使 Re ( G′c ( jω) ) a 2 + b 2 ≥δ,必须 使 KI < 0 , KD ≤0 ,3 KP - KI - 2 KD ≤0. 从而可知 ,本文针对小型无人机非线性被控对 象所设计的模糊自适应 PID 器 ,整体系统满足 I/ O 稳定的充分条件为 第 2 期 秦世引 ,等 :小型无人机纵向姿态模糊自适应 PID 控制与仿真 · 521 ·