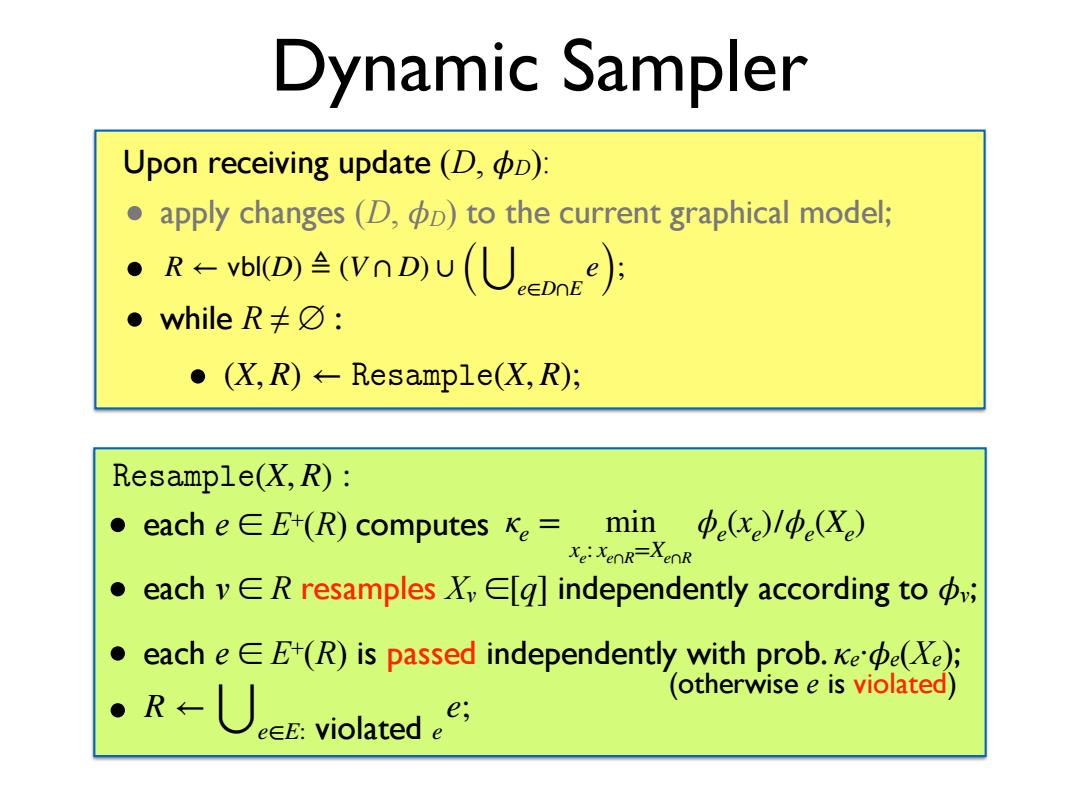
Dynamic Sampler Upon receiving update (D,D): apply changes(D,D)to the current graphical model; ·R←bD)(VnDu(UenE)月 ● while R≠⑦: ●(X,R)←-Resample(X,R); Resample(X,R): ● each e EE+(R)computes Ke= min 中xe)1φ(X) Xe:XenR-XenR ● each v ER resamples Xy E[g]independently according to ● each eE+(R)is passed independently with prob.ee(Xe); ·R←U,violated (otherwise e is violated)
Dynamic Sampler • apply changes (D, �D) to the current graphical model; • • while R ≠ ∅ : • R ← ���(D) ≜ (V ∩ D) ∪ (⋃e∈D∩E e); (X, R) ← ��������(X, R); ��������(X, R) : • each e ∈ E+(R) computes • each v ∈ R resamples Xv ∈[q] independently according to �v; • each e ∈ E+(R) is passed independently with prob. κe·�e(Xe); • R ← ⋃e∈E: violated e e; κe = min xe: xe∩R=Xe∩R ϕe(xe)/ϕe(Xe) Upon receiving update (D, �D): (otherwise e is violated)
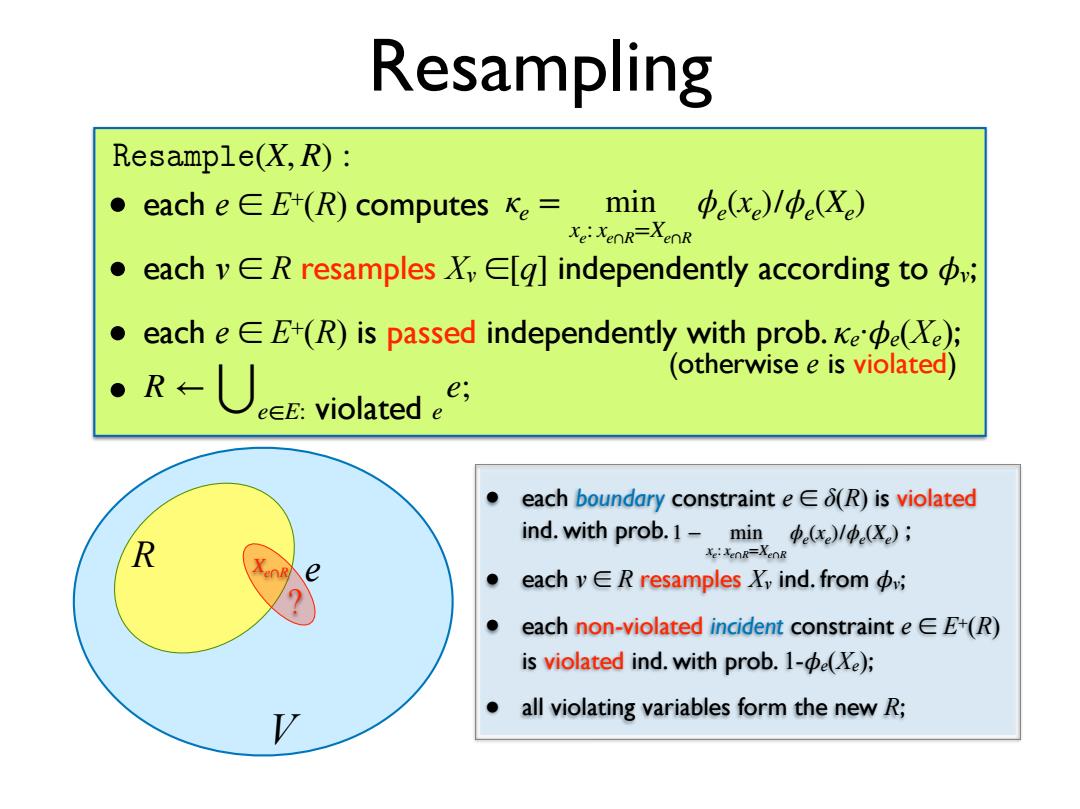
Resampling Resample(X,R): ● each eEE+(R)computes Ke= min中e(xe)/中e(Xe) Xe:XenR-XenR ● each vE R resamples X,E[q]independently according tov; ● each e EE+(R)is passed independently with prob.ee(Xe); ·R-U,violated (otherwise e is violated) ● each boundary constraint eE(R)is violated ind.with prob.1-min (x)/(X.); R Xe:XenR=XeoR e ● each vER resamples Xy ind.fromv; each non-violated incident constraint e EE+(R) is violated ind.with prob.1-e(Xe); all violating variables form the new R;
Resampling ��������(X, R) : • each e ∈ E+(R) computes • each v ∈ R resamples Xv ∈[q] independently according to �v; • each e ∈ E+(R) is passed independently with prob. κe·�e(Xe); • R ← ⋃e∈E: violated e e; κe = min xe: xe∩R=Xe∩R ϕe(xe)/ϕe(Xe) (otherwise e is violated) R V e Xe∩R ? • each boundary constraint e ∈ δ(R) is violated ind. with prob. ; • each v ∈ R resamples Xv ind. from �v; • each non-violated incident constraint e ∈ E+(R) is violated ind. with prob. 1-�e(Xe); • all violating variables form the new R; 1 − min xe: xe∩R=Xe∩R ϕe(xe)/ϕe(Xe)
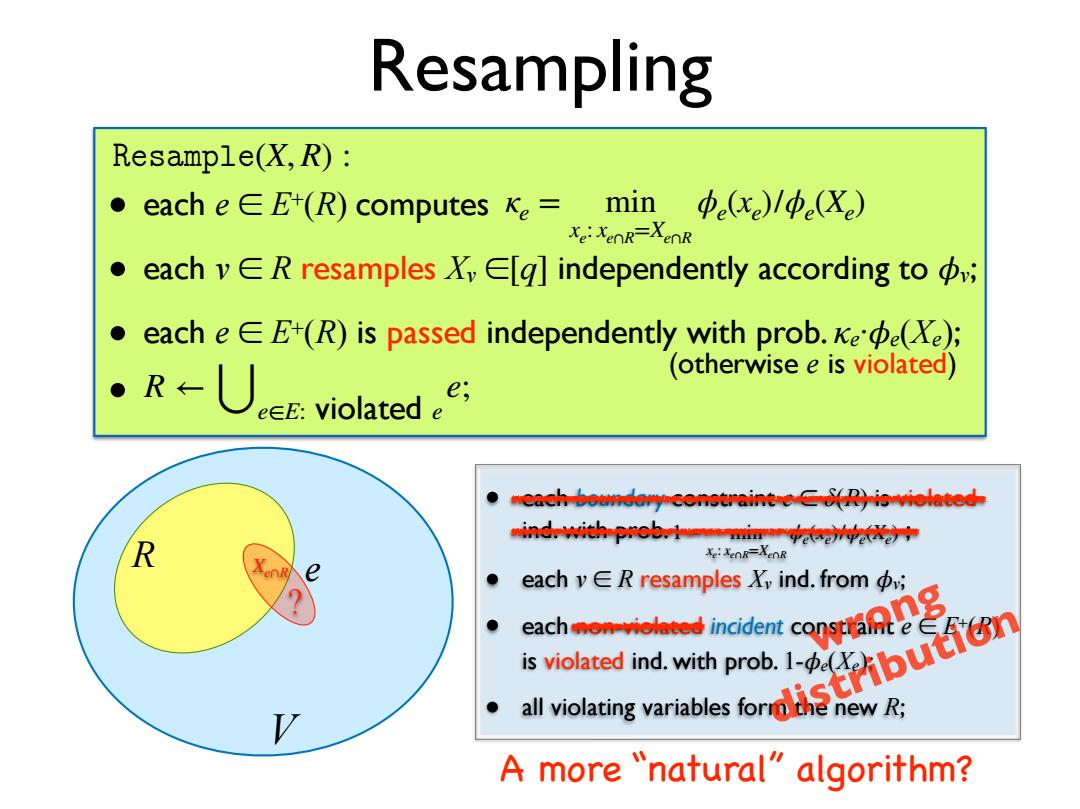
Resampling Resample(X,R): ● each eEE+(R)computes Ke= min中e(xe)/中e(Xe) Xe:XenR-XenR ● each vE R resamples Xy E[g]independently according to v; ● each e EE+(R)is passed independently with prob.ee(Xe); ·R-U,violated (otherwise e is violated) ncach-boundory)ioviolated ind.with prob.m R Xe:XeOR-XeoR e each v∈R resamples X,ind.from中; all vilating variabtes for ● e地noident co A more "natural"algorithm?
• each boundary constraint e ∈ δ(R) is violated ind. with prob. ; • each v ∈ R resamples Xv ind. from �v; • each non-violated incident constraint e ∈ E+(R) is violated ind. with prob. 1-�e(Xe); • all violating variables form the new R; 1 − min xe: xe∩R=Xe∩R ϕe(xe)/ϕe(Xe) Resampling ��������(X, R) : • each e ∈ E+(R) computes • each v ∈ R resamples Xv ∈[q] independently according to �v; • each e ∈ E+(R) is passed independently with prob. κe·�e(Xe); • R ← ⋃e∈E: violated e e; κe = min xe: xe∩R=Xe∩R ϕe(xe)/ϕe(Xe) (otherwise e is violated) R V e Xe∩R ? A more “natural” algorithm? wrong distribution