
己与X,聚成一类了,所以该步实际上是将X,X。X,聚为一类。 重复这一过程,直至将所有指标聚为一类为止。由于有8个指标,所以需要七步(第 四步至第七步聚类过程从略)。最终形成聚类图(谱系图)如图1-1所示。 0.5 17234658指标序号 图11-1聚类图(谱系图) 利用聚类图,我们就可以对指标进行精简了,若以r=0.8作为分类的阀值,则8个指 标可分为5类,X、X2、X,、(X、X)(X,、X。、X,如果第四类中选X,为 代表,舍掉X,第五类中选X,为代表,舍掉X,和X,那么最终的指标体系包括五个指 标:X、X2、X,、X,、X,。当然,若对指标体系的简约性要求较高,可以选低一些的 阙值,如选r=0.65,那么8个指标可分为三类即(X,、X,)、X2、(X,、X4、X、 X。、X,),第一类和第三类中各选一个代表指标(至于选哪一个,需要根据指标的性质及 经验决定),而将其它的指标删除,则最终的指标体系将由3个指标构成,这藏达到了我们 简化指标体系的目的。 第三种方法 主成分分析法 主成分分析就是设法将原来众多的具有一定相关性的指标(比如P个指标),重新组合成 一组新的相互无关的综合指标来代替原来的指标。通常数学上的处理就是将原米p个指标作 线性组合,若没有限制条件作为新的综合指标,这样的线性组合会有很多,那么如何去选取呢? 主成分分析的基本思想是:如果将选取的第一个线性组合即第一个综合指标记为下1,自然希 望下1尽可能多的反映原来指标的信息 这里的“信息”最经典的方法就 用F1的方差米 表达,即aFI)越大表示F1包含的信息越多。因此在所有的线性组合中所选取的F1应该 方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考 虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不在需要出现在 F2中用数学语言表达就是要求C。w(F12=0,称F2为第二主成分依次类推可以造出第三 四第。个主成分。不难相这此主成分之间 不仅不相关,而且它们的 差依次递减因此在 实际工作中,就挑选前几个最大主成分虽然这 部分信 抓住了主要 矛盾,并从原始数据中进一步提取了某些新的信息,这种既减少了变量的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。 主成分分析计算步骤如下:
6 已与 X5 聚成一类了,所以该步实际上是将 X5 X6 X8 聚为一类。 重复这一过程,直至将所有指标聚为一类为止。由于有 8 个指标,所以需要七步(第 四步至第七步聚类过程从略)。最终形成聚类图(谱系图)如图 1-1 所示。 0.5 1 7 2 3 4 6 5 8 指标序号 图 11-1 聚类图(谱系图) 利用聚类图,我们就可以对指标进行精简了,若以r = 0.8 作为分类的阈值,则 8 个指 标可分为 5 类, X1 、 X2 、 X7 、( X3 、 X4 )、( X5 、 X6 、 X8 ),如果第四类中选 X4 为 代表,舍掉 X3 ,第五类中选 X5 为代表,舍掉 X6 和 X8 ,那么最终的指标体系包括五个指 标: X1 、 X2 、 X7 、 X3 、 X5 。当然,若对指标体系的简约性要求较高,可以选低一些的 阈值,如选r = 0.65 ,那么 8 个指标可分为三类即( X1 、 X7 )、 X2 、( X3 、 X4 、 X5 、 X6 、 X8 ),第一类和第三类中各选一个代表指标(至于选哪一个,需要根据指标的性质及 经验决定),而将其它的指标删除,则最终的指标体系将由 3 个指标构成,这就达到了我们 简化指标体系的目的。 第三种方法:主成分分析法 主成分分析就是设法将原来众多的具有一定相关性的指标(比如 p 个指标),重新组合成 一组新的相互无关的综合指标来代替原来的指标。 通常数学上的处理就是将原来 p 个指标作 线性组合,若没有限制条件作为新的综合指标,这样的线性组合会有很多,那么如何去选取呢? 主成分分析的基本思想是:如果将选取的第一个线性组合即第一个综合指标记为 F1,自然希 望 F1 尽可能多的反映原来指标的信息。这里的“信息”最经典的方法就是用 F1 的方差来 表达,即 Var(F1)越大,表示 F1 包含的信息越多。 因此在所有的线性组合中所选取的 F1 应该是 方差最大的,故称 F1 为第一主成分。如果第一主成分不足以代表原来 p 个指标的信息,再考 虑选取 F2 即选第二个线性组合,为了有效地反映原来信息,F1 已有的信息就不在需要出现在 F2 中,用数学语言表达就是要求 Cov(F1,F2)=0,称 F2 为第二主成分,依次类推可以造出第三, 第四,第 p 个主成分。 不难想象这些主成分之间不仅不相关,而且它们的方差依次递减,因此在 实际工作中,就挑选前几个最大主成分"虽然这样做会损失一部分信息,但是由于抓住了主要 矛盾,并从原始数据中进一步提取了某些新的信息,这种既减少了变量的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。 主成分分析计算步骤如下:
①由己知的原始数据矩阵Xm计算样本均值向量户=x=(民,无,.,x)了;(11-1) 种=2,=12m ②计算样本协方差矩阵严= )(o,) (11-2) 其中号=-,-》j=l2,m) ③把原始数据标准化,即元,-一三,记文=传) (11-3) 形成样本相关矩阵=开: (11-4) ④求R的特征根入≥方≥.≥元≥0及相应的标准正交化的特征向量4,4,4。,可得 主成分为y=4x0=1,2,.,m) (11-5) [例如11-2]电子工业部所属的15个工厂某年份的经济效益数据如下表11-4。 其中:x一资金利税率(%):x,一固定资产利税率(%):x一流动资金利税率(%):x, 全员利税率(%):x,一成本利税率(%):x。一流动资金周转天数: 表11-4工厂的经济效益指标 厂序 69.87 269.10 94.38 115.74 23.85 66.31 260.00 89.01 93.30 40.09 67.26 272.54 89.29 78.90 26.70 号 4 68.46 250.18 94.24 76.87 24.98 39.45 146.17 54.04 90.95 17.46 109 67 81. 10.4 30.21 31.06 8 31.24 168.31 38.37 62.16 14.29 23.29 109.42 29.59 29.67 8.2% 23.10 92.41 30.80 43.57 12.48 136 1123 17.23 826 27.2 6.38 6 239 14 4.66 18.42 6.24 8.59 4.54 231 15 1.92 9.28 242 333 967 135
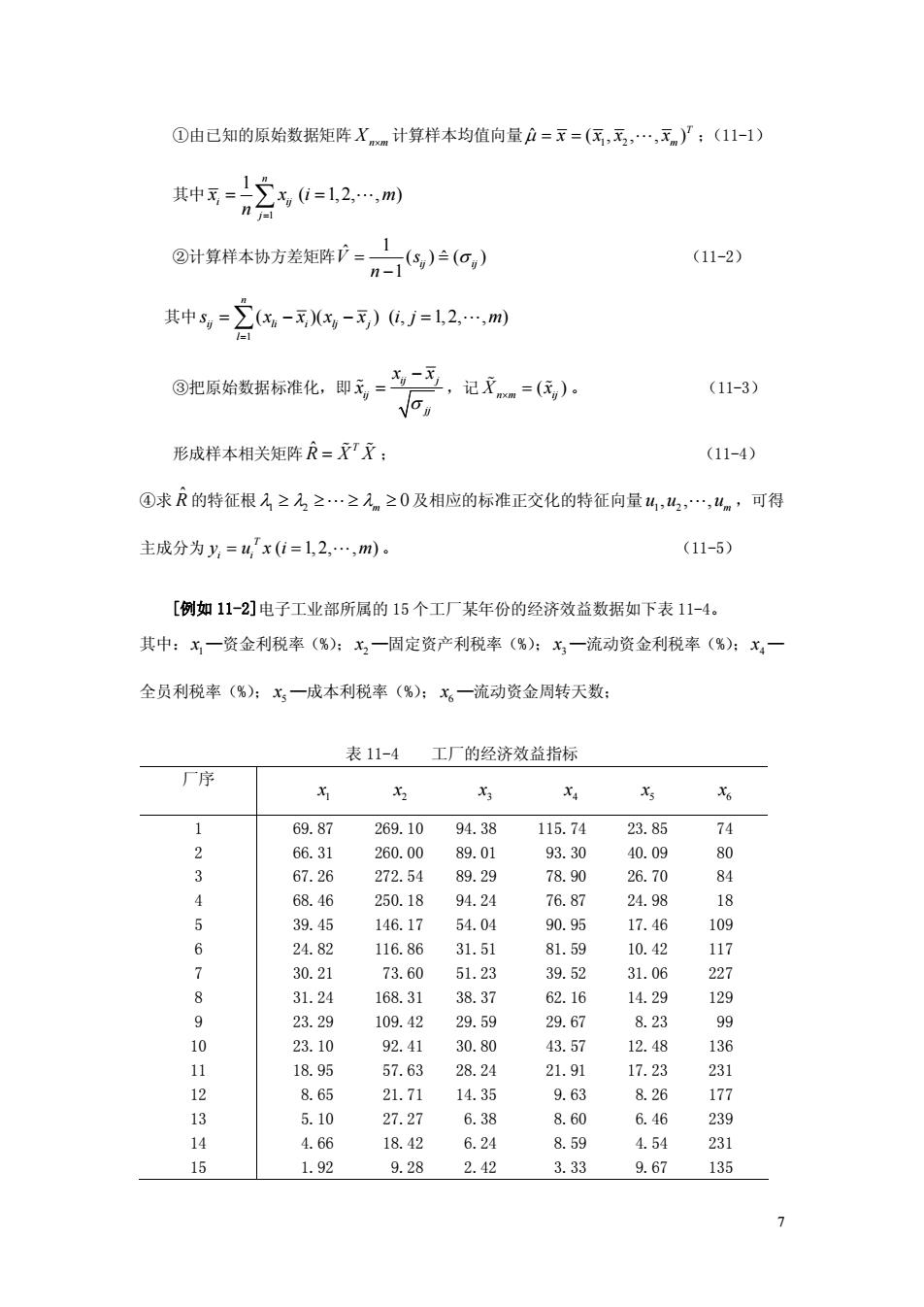
7 ①由已知的原始数据矩阵 Xn¥m 计算样本均值向量 1 2 ˆ ( , , , ) T m m = x = x x L x ;(11-1) 其中 1 1 ( 1,2, , ) n i ij j x x i m n = = Â = L ②计算样本协方差矩阵 1 ˆ ( ) ˆ ( ) 1 V ij ij s n = = s - (11-2) 其中 1 ( )( ) ( , 1, 2, , ) n ij li i lj j l s x x x x i j m = = Â - - = L ③把原始数据标准化,即 ij j ij jj x x x s - % = ,记 ( ) Xn m ij x ¥ = % % 。 (11-3) 形成样本相关矩阵 ˆ T R = X% X% ; (11-4) ④求 Rˆ 的特征根 1 2 0 l ³ l ³L ³ lm ³ 及相应的标准正交化的特征向量 1 2 , , , m u u L u ,可得 主成分为 ( 1, 2, , ) T i i y = u x i = L m 。 (11-5) [例如 11-2]电子工业部所属的 15 个工厂某年份的经济效益数据如下表 11-4。 其中: 1 x —资金利税率(%); 2 x —固定资产利税率(%); 3 x —流动资金利税率(%); 4 x — 全员利税率(%); 5 x —成本利税率(%); 6 x —流动资金周转天数; 表 11-4 工厂的经济效益指标 厂序 1 x 2 x 3 x 4 x 5 x 6 x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 69.87 269.10 94.38 115.74 23.85 74 66.31 260.00 89.01 93.30 40.09 80 67.26 272.54 89.29 78.90 26.70 84 68.46 250.18 94.24 76.87 24.98 18 39.45 146.17 54.04 90.95 17.46 109 24.82 116.86 31.51 81.59 10.42 117 30.21 73.60 51.23 39.52 31.06 227 31.24 168.31 38.37 62.16 14.29 129 23.29 109.42 29.59 29.67 8.23 99 23.10 92.41 30.80 43.57 12.48 136 18.95 57.63 28.24 21.91 17.23 231 8.65 21.71 14.35 9.63 8.26 177 5.10 27.27 6.38 8.60 6.46 239 4.66 18.42 6.24 8.59 4.54 231 1.92 9.28 2.42 3.33 9.67 135