
问题提出和模型建立 问题提出 2T S3 •盲目搜索?按某种顺序搜索? •如何判断是否得到最短路径? S4 S5 S6 0 模型建立 •图模型的建立 S7 S8 S9■ Sg ·每个格子及入口和出口都作为节点 •通道作为边 •构成有向图 Hangzhou Dianzi University杭州电子科技大学 Schoofo时Computer Science and Tecfinology计算机学院周文晖
Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 问题提出和模型建立 问题提出 •盲目搜索?按某种顺序搜索? •如何判断是否得到最短路径? 模型建立 •图模型的建立 •每个格子及入口和出口都作为节点 •通道作为边 •构成有向图
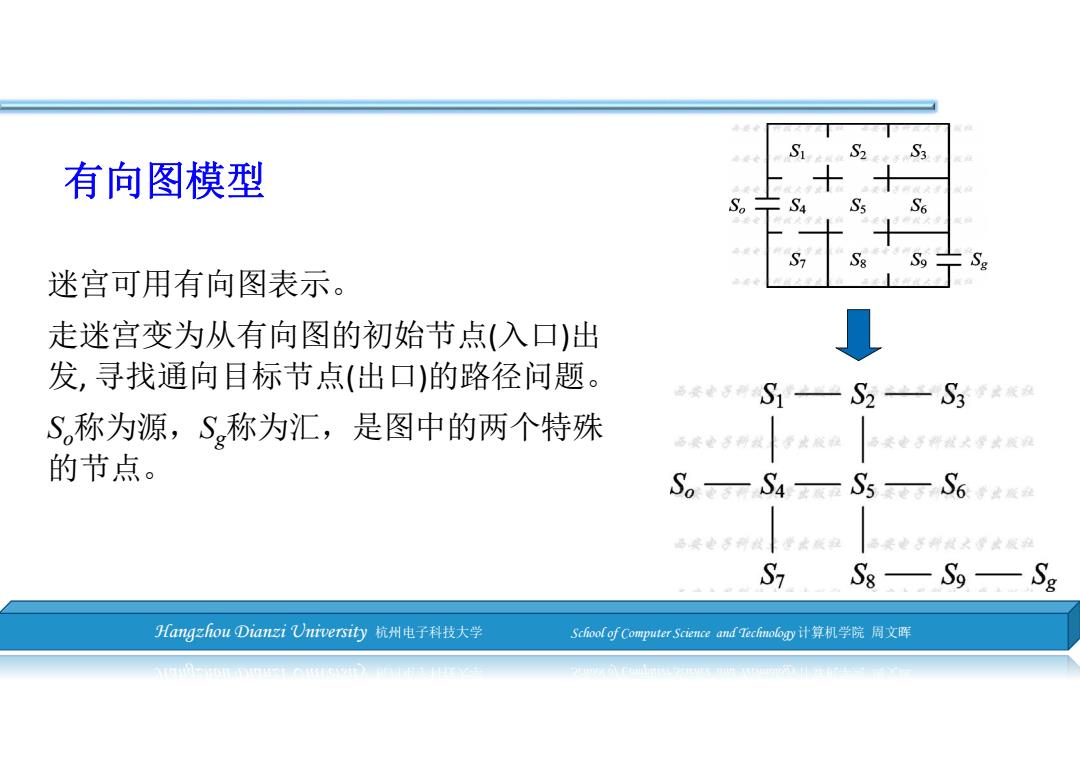
有向图模型 S S 迷宫可用有向图表示。 走迷宫变为从有向图的初始节点(入口)出 发,寻找通向目标节点(出口)的路径问题。 西安电子科 S1一S2一S3 登其发应 S称为源,S称为汇,是图中的两个特殊 6套电多份 学女税自 西买电子背发大堂其夜阻 的节点。 S。S4- S5一 S6 S1 Sg Hang2 hou Dian2 iUniversity杭州电子科技大学 Schoof of Computer Science and Tecfmology计算机学院周文晖
Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 有向图模型 迷宫可用有向图表示。 走迷宫变为从有向图的初始节点(入口)出 发, 寻找通向目标节点(出口)的路径问题。 So称为源,Sg称为汇,是图中的两个特殊 的节点

八数码问题/华容道/拼图 赵云 问题描述: 黄忠 曹操 ·在一个3×3的方格棋盘上放置着1,2,3,4,5,6,7, 8八个数码,每个数码占一格,且有一个空格。 马超 •从初始棋局到目标棋局 张飞 2 8 3 8 1 3 1 4 2 大受 4 关羽 6 5 7 6 5 黄刀立 初始棋局 目标棋局 Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and Tecfinology计算机学院周文晖
Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 八数码问题/华容道/拼图 问题描述: •在一个3×3的方格棋盘上放置着1, 2, 3, 4, 5, 6, 7, 8八个数码, 每个数码占一格, 且有一个空格。 •从初始棋局到目标棋局

拓扑图模型 技巧:逆向思维,棋子移动等效于空格移动 图中的一条边(即相邻两个节点的连线)对应一次移动。 一次移动也对应着图中的一条边。 但移动是按规则进行的。 所以图中的一条边也代表了一个移动规则或移动规则的一次执行。 八数码问题也就是要在该拓扑图中寻找目标节点,或找一条从初始节 点到目标节点的路径问题。 Hangzhou Dianzi University杭州电子科技大学 Schoolo时Computer Science and Tecfmnology计算机学院周文晖
Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 拓扑图模型 技巧:逆向思维,棋子移动等效于空格移动 图中的一条边(即相邻两个节点的连线) 对应一次移动。 一次移动也对应着图中的一条边。 但移动是按规则进行的。 所以图中的一条边也代表了一个移动规则或移动规则的一次执行。 八数码问题也就是要在该拓扑图中寻找目标节点, 或找一条从初始节 点到目标节点的路径问题

状态图搜索方法 问题求解转换为状态图搜索过程。 搜索的效率(速度和准确性)是关键。 两种搜索方法 •树式搜索 •线式搜索 Hangzhou Dianzi University杭州电子科技大学 School of Computer Science and1 ecfmology计算机学院周文晖
Hangzhou Dianzi University 杭州电子科技大学 School of Computer Science and Technology 计算机学院 周文晖 状态图搜索方法 问题求解转换为状态图搜索过程。 搜索的效率(速度和准确性)是关键。 两种搜索方法 •树式搜索 •线式搜索