
第27卷第5期 作物学报 Vol.27,No.5 2001年9月 ACTA AGRONOMICA SINICA Sept.,2001 线性回归分析的逆预测' 莫惠栋 (扬州大学数量遗传研究室,江苏扬州225009) 提要逆预测又称逆回归,是从依靠变数Y的某一定值Y,预测独立变数X的对应值X。及其100(1 一)%可信区间。本文详细地解释了逆回归的原理、方法和注意问题,推导了逆回归的一些基本公式, 并用两个实例分别说明Y。为Y总体的条件平均数和单一观察值时的逆回归程序。 关键词线性回归:逆回归 Inverse Prediction in Linear Regression Analysis MO Hui-Dong (Lab of Quantitative Genctics.Yangshou Uniwersity.Yangshou 225009.China) Abstract The inverse prediction,i.e.,inverse regression,which is predicting an inde pendent variate Xo and its 100(1-a)%fiducial limits from a given value Yo of dependent variable Y.In the present paper,the principle and method for inverse regression were ex- plained and some fundamental formulae were derived and extended.Two real examples were taken to demonstrate the inverse regression procedure when Yo was a conditional mean and a single observed variate of Y population,respectively. Key words Inverse regression:Linear regressior 回归分析是处理具有自变数(X)和依变数(Y)之分的试验资料的统计方法,通常要求X 固定,Y随机。所以分析的基本目的是由X估计或预测Y,其k元线性回归模型的一般形式 为Y,=a十b,X+e(i=1,2,,k;j=1,2,…,n)们。但是,在有些情况下,研究者需要 了解的却是Y在某一Y。时的X值及其置信区间。例如:在农用药物的毒力测定中,药品浓 度是X变数,昆虫死亡率是Y变数,如欲得到半致死浓度(Y=50%时的药品浓度),就必须 从Y反推X:在树龄测定中,年轮数是X变数,“碳记年”是Y变数,由碳记年估计树木年龄 也是由Y反推X。很多仪表的校准(calibration)亦属由Y(仪表读数)预测X(标的物状况)。 在近代遗传学研究中,QTL的定位也是要从Y(表型值)估计X(基因座位位置)。这类从Y反 推、估计或预测X的分析,统称为逆回归或逆预测,其统计原理和方法国内尚未见报道。本 文将阐述逆回归的意义,推导其区间估计,并以实例说明演算过程,以供应用和深入理解某 些涉及逆回归的问题。文中所用符号和公式,除特别说明外,都按照文献[1],不再解释。 接受日期 0-09.25 Received on:2000-08-14.Accepted on:2000-09-25
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 第 "#卷 第 $期 作 物 学 报 %&’("#)*&($ "++,年 -月 ./0. .123*345/. 65*5/. 6789()"++, 线性回归分析的逆预测: 莫 惠 栋 ;扬州大学数量遗传研究室)江苏扬州 ""$++-< 提 要 逆预测又称逆回归)是从依靠变数 =的某一定值 =+预测独立变数 >的对应值 >+及其 ,++;, ?@<A可信区间B本文详细地解释了逆回归的原理C方法和注意问题)推导了逆回归的一些基本公式) 并用两个实例分别说明 =+为 =总体的条件平均数和单一观察值时的逆回归程序B 关键词 线性回归D逆回归 EFGHIJHKIHLMNOMPFMFQMFHRISHTIHJJMPFUFRVWJMJ 43XYZ[\&]^ ;_‘abcde‘fghg‘ghijkjfjghlm)=‘fnopbeqfhijrmhgs)=‘fnopbe""$++-)tphf‘< UuJOIRNO 0v7Z]w7xy78x7zZ{9Z&])Z(7()Z]w7xy7x7^x7yyZ&])|vZ{vZy8x7zZ{9Z]^}]Z]z7[ 87]z7]9w}xZ}97>+ }]zZ9y,++;,? ~<A !ZzY{Z}’’Z"Z9y!x&" }^Zw7]w}’Y7=+ &!z787]z7]9 w}xZ}#’7=(5]9v78x7y7]98}87x)9v78xZ]{Z8’7}]z"79v&z!&xZ]w7xy7x7^x7yyZ&]|7x77$[ 8’}Z]7z}]zy&"7!Y]z}"7]9}’!&x"Y’}7|7x7z7xZw7z}]z7$97]z7z(0|&x7}’7$}"8’7y|7x7 9}%7]9&z7"&]y9x}979v7Z]w7xy7x7^x7yyZ&]8x&{7zYx7|v7]=+|}y}{&]zZ9Z&]}’"7}]}]z} yZ]^’7&#y7xw7zw}xZ}97&!=8&8Y’}9Z&])x7y87{9Zw7’&( ’HW(PILJ 5]w7xy7x7^x7yyZ&]D)Z]7}xx7^x7yyZ&] 回归分析是处理具有自变数;><和依变数;=<之分的试验资料的统计方法)通常要求 > 固定)=随机B所以分析的基本目的是由 >估计或预测 =)其 *元线性回归模型的一般形式 为 =+,‘-.ah>h+-j+;h,,)")/)*D+,,)")/)f<0,1 B但是)在有些情况下)研究者需要 了解的却是 =在某一 =+时的 > 值及其置信区间B例如2在农用药物的毒力测定中)药品浓 度是 >变数)昆虫死亡率是 =变数)如欲得到半致死浓度;=,$+A时的药品浓度<)就必须 从 =反推 >D在树龄测定中)年轮数是 >变数)3碳记年4是 =变数)由碳记年估计树木年龄 也是由 =反推 >B很多仪表的校准;{}’Z#x}9Z&]<亦属由 =;仪表读数<预测 >;标的物状况<B 在近代遗传学研究中)50)的定位也是要从 =;表型值<估计 >;基因座位位置<B这类从 =反 推C估计或预测 >的分析)统称为逆回归或逆预测)其统计原理和方法国内尚未见报道B本 文将阐述逆回归的意义)推导其区间估计)并以实例说明演算过程)以供应用和深入理解某 些涉及逆回归的问题B文中所用符号和公式)除特别说明外)都按照文献0,1)不再解释B : 国家自然科学基金;6-7#+6-,<项目资助 收稿日期2"+++[+8[,9)接受日期2"+++[+-["$ 27{7Zw7z&]2"+++[+8[,9).{{7897z&]2"+++[+-["$ 万方数据

546 作物学 报 27卷 1原理和公式 在一元线性回归中,Y依X的条件总体平均数x由 Y=a+bX % 估计;其对x的100(1-a)%置信带由 y士=y士[片+X (2) 给出。当 Y=Y。 (3) 时,以上3个方程的几何轨迹可见图1。图1上 3个交点所对应的X轴坐标值:X。表示对应于 Y。的X估计值:X和X分别表示对应于Y。 的X,的100(1一a)%可信限((fiducial limits)回 或逆置信限((inverse confidence limits)的低限 和高限。[X,X,]则称为逆回归的100(1 a)%可信区间或预测区间。 估计X。是方便的,因为根据(1)可有Y。=a +bX。,故 X。=(Y。-a)/b。 (4) 对于X和X的估计,可推导如下:低限X上 的“高度”Y可表示为: Y=Y。=a+bXo, (5) 图】逆回归的几何意义 和Y=a+bX-x+X-7 x。(6) Fig.】Geomerica or inverse regreo,令(5)=(6),并左右平方可得: i.e..predicting Xo.X and Xe given Yo x,-6xr=[片+] (7) 同理,对高限X“上的“高度”亦可得 (8) 上述(7)和(8)除X和X,的区别外,其余完全相同;若以X代X,或X,均可写成二次 三项式: AX:+BX+C=0. (9) A=b-tx/x2,B=2xtx/∑x2-2bX。 其中 (10) C=bXi-tisi/n-tisix/Ex2 因此,解(9)得到X的两个根即分别为X和X。 万方数 g=s号x/Bx (11) 化(10),再代回 (9)即可解得
! 原理和公式 在一元线性回归中"#依 $的条件总体平均数 %#&$由 # ’( )* +$ ,-. 估计/其对 %#&$的 -00,-12.3置信带由 # ’4 526# ’( # ’4 526#&$ - 7* ,$1 8 9.: < ;8: = -&: ,:. 给出>当 #( #0 ,?. 图 - 逆回归的几何意义 @ABC- DEFGEHIAJKLEMNLKOKHAFOPFIAOQEIREIEBIERRAFO" SCTC"NIEUAJHAOB$0"$V KOU$W BAQEO#0 时"以上 ?个方程的几何轨迹可见图 ->图 -上 ?个交点所对应的 $ 轴坐标值X$0表示对应于 #0的 $ 估计值/$V 和 $W 分别表示对应于 #0 的 $0的 -00,-12.3可信限,PAUYJAKLLAGAHR.<:= 或逆置信限,AOQEIREJFOPAUEOJELAGAHR.<?=的低限 和 高 限><$V"$W=则 称 为 逆 回 归 的 -00,-1 2.3可信区间或预测区间> 估计 $0是方便的"因为根据,-.可有 #0() *+$0"故 $0( ,#01 ).&+> ,Z. 对于 $V 和 $W 的估计"可推导如下X低限 $V 上 的[高度\#可表示为X #( #0( )* +$0" ,]. 和 #()*+$V1526#&$ - 7*,$V18 9.: < ;8: = -&: >,^. 令,].(,^."并左右平方可得X ,+$01 +$V.:( 5: 26: #&$ - 7* ,$V 1 8 9.: < ;8: => ,_. 同理"对高限 $W 上的[高度\亦可得X ,+$01 +$W.:( 5: 26: #&$ - 7* ,$W 1 8 9.: < ;8: => ,‘. 上述,_.和,‘.除 $V 和 $W 的区别外"其余完全相同/若以 $代 $V 或 $W"均可写成二次 三项式X a$:* b$* c( 0> ,d. 其中 a(+: 15: 26: #&$&;8: "b(:85: 26: #&$&;8: 1:+: $0 c(+: $: 015: 26: #&$&718: 5: 26: #&$&;8 e f g : > ,-0. 因此"解,d.得到 $的两个根即分别为 $V 和 $W> 令 h( 5: 26: #&$&+: ;8: ,--. 简化,-0."再代回,d.即可解得X ]Z^ 作 物 学 报 :_卷 万方数据

5期 莫惠栋:线性回归分析的逆预测 Xx-图-x-a±01- (12 其中 d-[=®+] x2 (13) 2推户 上述是Y。为条件总体平均数4x的逆回归,可推广于 2.1Y。仅是Y的一个观察值的逆回归 由于Y的标准误为: =wx[1+}+-7 x2」 。 (14) 这一改变仅使应用(12)于估计X。和X时的d值改变为: d-[1-0+2] (15) 2.2Y。是m个Y值的平均值的逆回归 仍应用(I2)估计X。和X,但d改变为: d=名[品+1-)+-] (16) x2 2.3Y。是多元线性回归依变数的逆回归 上述原理和方法也可能推广到多元线性回归模型,这里只作概述。k元线性回归方程Y =a十b,X1十b2X2十…+bX的逆回归,即求Y=Y。时k维空间点(Xo,X0,…,X)的可信 区((fiducial region)。由于k元回归中Y和Y的标准误可以一般化地写作): s=5yxxX(X'X)-Xo] sy=yxx.x,1+X。(XX)-X]e了 (17) (17)中的X为X变数的nX(k十1)阶矩阵,X。为X的列向量,即X。=(1,Xo,X0,, X0)。而前述令(5)=(6)并左、右平方也可写成: [Y。-(a+bX)]=ts5。 (18) 故推广于k元回归时,若Y。是条件总体平均数X。,则X可信区的界面满足方程: [Y。-(a+bX1+bX2+…+bX)]=sx,m.x,[X(X'X)-1X]。 (19) 若Y。是单一观察值则满足方程: [Y。-(a+bX,+bX:+…+hX,)]=8xx-x[1+X,(X'X)-X,]。(20) 异常和原因 逆回归可能出现一些异常情况,例如:(1)X,和X,为复数,其几何图形是Y=Y。与置 信带的双曲线不相交,如图2(a):(2)X,和X,虽为实数,但其间不包含X。,如图2(b)。以 上逆回归显然都没有实际意义。其原因是回归的线性不强,使置信带双曲线迅速偏离回归直 线,以及测晚远离回归中心工。这可通过对g和(X。一五)的分析得到了解
!" !# ! $ % & (’ " )*!+, -./0 123*4, -/5 *46/ 其中 1"789:3! ; *4,-/ < =*!+,./6 ) >.6 2 436 ? *4@/ A 推广 上述是 :+为条件总体平均数 B:3!的逆回归5可推广于C ADE FG仅是 F的一个观察值的逆回归 由于 :的标准误为C 9: " 9:3! 4= 4 <= *!+, ./6 ) >.6 2 436 ? *4H/ 这一改变仅使应用*46/于估计 !# 和 !( 时的 1值改变为C 1" 789:3! ; <= 4 < *4, -/= *!+, . I/6 ) >.6 2 436 ? *4J/ ADA FG是 K个 F值的平均值的逆回归 仍应用*46/估计 !# 和 !(5但 1改变为C 1" 789:3! ; 4 L = 4 M <N*4, -/= *!+, ./6 ) >.6 2 436 ? *4O/ ADP FG是多元线性回归依变数的逆回归 上述原理和方法也可能推广到多元线性回归模型5这里只作概述?Q元线性回归方程 : R "S=;4!4=;6!6=T=;Q!Q的逆回归5即求 :":+时 Q维空间点*!4+5!6+5T5!Q+/的可信 区*UVWXYVZ[\]^V_‘/?由于 Q元回归中 : R和 :的标准误可以一般化地写作)@2 C 9: R" 9:3!45!65T5!Q)ab +*aba/,4 a+2436 9: " 9:3!45!65T5!Q)4= ab +*aba/,4 a+2 c & ’436 ? *4d/ *4d/中的 a为 ! 变数的 <e*Q=4/阶矩阵5a+为 !f+的列向量5即 ab +"*45!4+5!6+5T5 !Q+/?而前述令*J/"*O/并左g右平方也可写成C ):+, *S= ;!/26" 76 896 : R? *4h/ 故推广于 Q元回归时5若 :+是条件总体平均数 B:3!f+5则 !f+可信区的界面满足方程C ):+, *S= ;4!4= ;6!6= T = ;Q!Q/26" 76 896 :3!45!65T5!Q)ab +*aba/,4 a+2? *4i/ 若 :+是单一观察值则满足方程C ):+, *S= ;4!4= ;6!6= T = ;Q!Q/26" 76 896 :3!45!65T5!Q)4= ab +*aba/,4 a+2? *6+/ P 异常和原因 逆回归可能出现一些异常情况5例如C*4/!( 和 !# 为复数5其几何图形是 :":+与置 信带的双曲线不相交5如图 6*Z/j*6/!( 和 !# 虽为实数5但其间不包含 !+5如图 6*k/?以 上逆回归显然都没有实际意义?其原因是回归的线性不强5使置信带双曲线迅速偏离回归直 线5以及预测的 !+远离回归中心 .?这可通过对 -和*!+,./的分析得到了解? J期 莫惠栋C线性回归分析的逆预测 JHd 万方数据
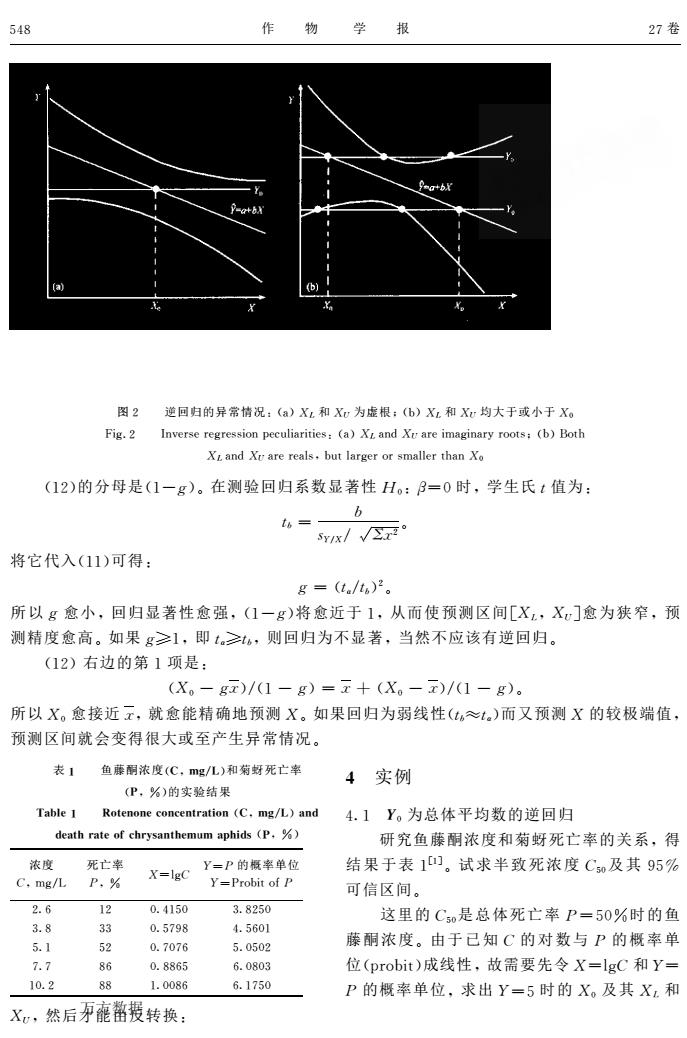
548 物 学 27卷 图2逆回归的异常情况:(a)X和X为虚根,(b)X和Xr均大于或小于X。 Fig.2 Inverse regression peculiarities:(a)X and X are imaginary roots (b)Both Xt and Xr are reals.but larger or smaller than Xo (12)的分母是(1一g)。在测验回归系数显著性H。:B=0时,学生氏1值为: w= Synx/x 将它代入(11)可得: g=(t./ts)2。 所以g愈小,回归显著性愈强,(1一g)将愈近于1,从而使预测区间[X,X]愈为狭窄,预 测精度愈高。如果g≥1,即t≥4,则回归为不显著,当然不应该有逆回归。 (12)右边的第1项是: (X。-gz)/(1-g)=五+(X。-x)/(1-g)。 所以X。愈接近云,就愈能精确地预测X。如果回归为弱线性(≈)而又预测X的较极端值, 预测区间就会变得很大或至产生异常情况。 表】鱼藤浓度(C,mg/L)和菊蚜死亡率 4实例 (P,⅓)的实验结果 Table 1 Rotenone concentration (C.mg/L)and 4.1Y。为总体平均数的逆回归 death rate of chrysanthemum aphids (P.%) 研究鱼藤酮浓度和菊蚜死亡率的关系,得 浓度 死亡率 y三P的概率单位 X=lgC 结果于表1。试求半致死浓度C及其95% C,mg/LP,⅓ Y=Probit of P 可信区间。 2.6 12 0.4150 3.8250 3.8 .560 这里的C是总体死亡率P=50%时的鱼 5.1 藤酮浓度。由于已知C的对数与P的概率单 0.7070 5.0502 7.7 86 0.8865 6.0803 位(probit)成线性,故需要先令X=lgC和Y= 10.2 88 1.0086 6.1750 P的概率单位,求出Y=5时的X。及其X和 X,然后界能蕃授转换:
图 ! 逆回归的异常情况"#$%&’和 &( 为虚根)#*%&’和 &( 均大于或小于 &+ ,-./! 012345343.4355-617389:-$4-;-35"#$%&’ $1<&( $43-=$.-1$4>466;5)#*%?6;@ &’ $1<&( $4343$:5A*9;:$4.34645=$::34;@$1&+ #B!%的分母是#BCD%E在测验回归系数显著性 F+"GH+时A学生氏 I值为" IJH J KLM&MPNO!E 将它代入#BB%可得" DH #IQMIJ%! E 所以 D愈小A回归显著性愈强A#BCD%将愈近于 BA从而使预测区间R&’A&(S愈为狭窄A预 测精度愈高E如果 DTBA即 IQTIJA则回归为不显著A当然不应该有逆回归E #B!%右边的第 B项是" #&+C DO%M#BC D%H OU #&+C O%M#BC D%E 所以 &+愈接近 OA就愈能精确地预测 &E如果回归为弱线性#IJVIQ%而又预测 &的较极端值A 预测区间就会变得很大或至产生异常情况E 表 W 鱼藤酮浓度#XAYZM[%和菊蚜死亡率 #\A]%的实验结果 ^_‘abW cdebfdfbgdfgbfeh_eidf#XAYZM[%_fj jb_ekh_ebdlgkhmn_fekbYoY _pkijn#\A]% 浓度 qA=.Mr 死亡率 sA] &H:.q LHs的概率单位 LHt46*-;6us !/v B! +/wBx+ y/z!x+ y/z yy +/x{|z w/xv+B x/B x! +/{+{v x/+x+! {/{ zv +/zzvx v/+z+y B+/! zz B/++zv v/B{x+ } 实例 w/B ~+为总体平均数的逆回归 研究鱼藤酮浓度和菊蚜死亡率的关系A得 结果于表 BRBS E试求半致死浓度 qx+及其 |x! 可信区间E 这里的 qx+是总体死亡率 sHx+]时的鱼 藤酮浓度E由于已知 q的对数与 s的概率单 位#746*-;%成线性A故需要先令 &H:.q和 LH s的概率单位A求出 LHx时的 &+及其 &’ 和 &(A然后才能由反转换" xwz 作 物 学 报 !{卷 万方数据

5期 莫惠栋:线性回归分析的逆预测 549 C=anti le x 得到C等。 从表1的X和Y得到:z=0.7195,y=5.13812,x2=0.223846,y2=4.028944,xy =0.938747,Y=2.120737+4.193721X,5yx=0.175216。查t表,df=5-2=3时,ts= 3.182。因此,根据(4)、(11)、(13)和(12)依次有: X。=(5-2.120737)/4.193721=0.686565, g=(3.1822×0.1752162)/(4.1937212×0.223846 =0.078959 d=3.182×0.1752161-0.078959+0.686565-0.7195)27 4.193721 0.223846 =0.057805 X。=[(0.686565-0.078959×0.7195)+0.057805]/(1-0.078959)=0.746502, X=[(0.686565-0.078959×0.7195)-0.057805]/(1-0.078959)=0.620981 以上结果说明:鱼藤酮对菊蚜的半致死浓度为 表2 水流流率(X,m3/see)】 Cso=antilg0.686565=4.86mg/L;其95%可信高限 和流率仪读数(y) 为antilg0.746502=5.58mg/L,低限为antilg Table 2 Flow rate (X.m2/sec) 0.620981=4.18mg/L。 and readings on a flow meter (Y) 4.2Y。为单一观察值的逆回归 y 研究灌溉水流率和流率仪读数的关系,得表2结 果。某次测定读得Y。=4.0,求流率X。及其95%可 信限。 4.2 从表2可得回归分析的基本数据:x=5.5,y= 5.8 5.45,x2=82.5,y2=67.065,xy=74.35和Y= 6.8 7.6 0.493333+0.901212X,sx=0.086503。df=8时的 8.7 as=2.306。故根据(4)、(11)、(15)和(12)依次有: 10 9.5 X。=(4.0-0.493333)/0.901212=3.8911m3/sec, g=(2.3062×0.0865032)/(0.9012122×82.5)=0.000594, -2306X0.086503TLX0.909406士③.8911-5.5)7 0.901212 82.5 =0.2354 X。-g元=3.8911-(0.000594×5.5)=3.8878, 所以,X=(3.8878+0.2354)/0.999406=4.1256m3/sec, X=(3.8878-0.2354)/0.999406=3.6546m3/sec。 参考文献 1莫惠栋.农业试验统计.上海:上海科学技术出版社,1992.308~329,510~526 2 Williums EJ.Regression Analysis.New York:John Wiley 8.Sons.Inc..1959.Chapt.6 3 Draper N R.H Smith.Applied Regression Analysis.New York:John Wiley &Sons.Inc..1998.47~51 4 Ott R L.An introduction to statistical Methods and Data Analysis.Belmont.California:Duxbury Press.Wadsworth Inc.,1993.437-563 XXX万右数据XX和和
!" #$%&’() 得到 !*+等, 从表 -的 )和 .得到/0"+12-3*45"*1-67-84908 "+18867:;4958 ":1+873::4905 "+13672:24. <"81-8+262=:1-3628-)4>.?)"+1-2*8-;,查 @表4AB"*C8"6时4@+1+*" 61-78,因此4根据D:EFD--EFD-6E和D-8E依次有/ )+" D*C 81-8+262E?:1-3628-" +1;7;*;*4 G" D61-788H +1-2*8-;8 E?D:1-3628-8H +18867:;E" +1+273*34 A" 61-78H +1-2*8-; :1-3628- -C +1+273*3 * = D+1;7;*;*C +12-3*E8 I +18867:; J -?8 " +1+*27+*4 )K " ID+1;7;*;*C +1+273*3H +12-3*E= +1+*27+*J?D-C +1+273*3E" +12:;*+84 )L " ID+1;7;*;*C +1+273*3H +12-3*EC +1+*27+*J?D-C +1+273*3E" +1;8+37-, 表 M 水流流率DN4OP?QRSE 和流率仪读数DTE UVWXRM YXZ[\V]RDN4OP?QRSE V^_\RV_‘^aQZ^VbXZ[OR]R\DTE ) . - -1: 8 816 6 61- : :18 * *1- ; *17 2 ;17 7 21; 3 712 -+ 31* 以上结果说明/鱼藤酮对菊蚜的半致死浓度为 !*+"#$%&’(+1;7;*;*":17;c(?de其 3*f可信高限 为 #$%&’( +12:;*+8" *1*7c(?d4低 限 为 #$%&’( +1;8+37-":1-7c(?d, g1M Th为单一观察值的逆回归 研究灌溉水流率和流率仪读数的关系4得表 8结 果I:J ,某次测定读得 .+":1+4求流率 )+及其 3*f可 信限, 从表 8可得回归分析的基本数据/0"*1*45" *1:*4908 "781*4958 ";21+;*4905"2:16*和 . <" +1:36666=+13+-8-8)4>.?)"+1+7;*+6,AB"7时的 @+1+*"816+;,故根据D:EFD--EFD-*E和D-8E依次有/ )+" D:1+C +1:36666E?+13+-8-8" 6173--c6 ?ijk4 G" D816+;8H +1+7;*+68 E?D+13+-8-88H 781*E" +1+++*3:4 A" 816+;H +1+7;*+6 +13+-8-8 --H +1333:+; -+ = D6173--C *1*E8 I 781* J -?8 " +186*:4 )+C G0" 6173--C D+1+++*3:H *1*E" 6177274 所以4 )K"D617727=+186*:E?+1333:+;":1-8*;c6 ?ijk4 )L"D617727C+186*:E?+1333:+;"61;*:;c6 ?ijk, 参 考 文 献 - 莫惠栋1农业试验统计1上海/上海科学技术出版社4-33816+7l6834*-+l*8; 8 m&’’&nciop1qrGsr>>tuvwvxy5>t>1zj{|}~!/p}"$m&’j#$%}$i4&$k14-3*31’"#(%1; 6 )~#(j~z *4+ %c&%"1w,,ytrAqrGsr>>tuvwvxy5>t>1zj{|}~!/p}"$m&’j#$%}$i4&$k14-3371:2l*- : -%%* d1wvtv@suA./@tuv@u>@x@t>@t/xy0r@1uA>xvA2x@xwvxy5>t>13j’c}$%4’#’&4}~$&#/)n56n~#7~jii4m#8i{}~%" &$k14-3361:62l*;6 )K )K )K )K )K )K)K )K )K *期 莫惠栋/线性回归分析的逆预测 *:3 万方数据