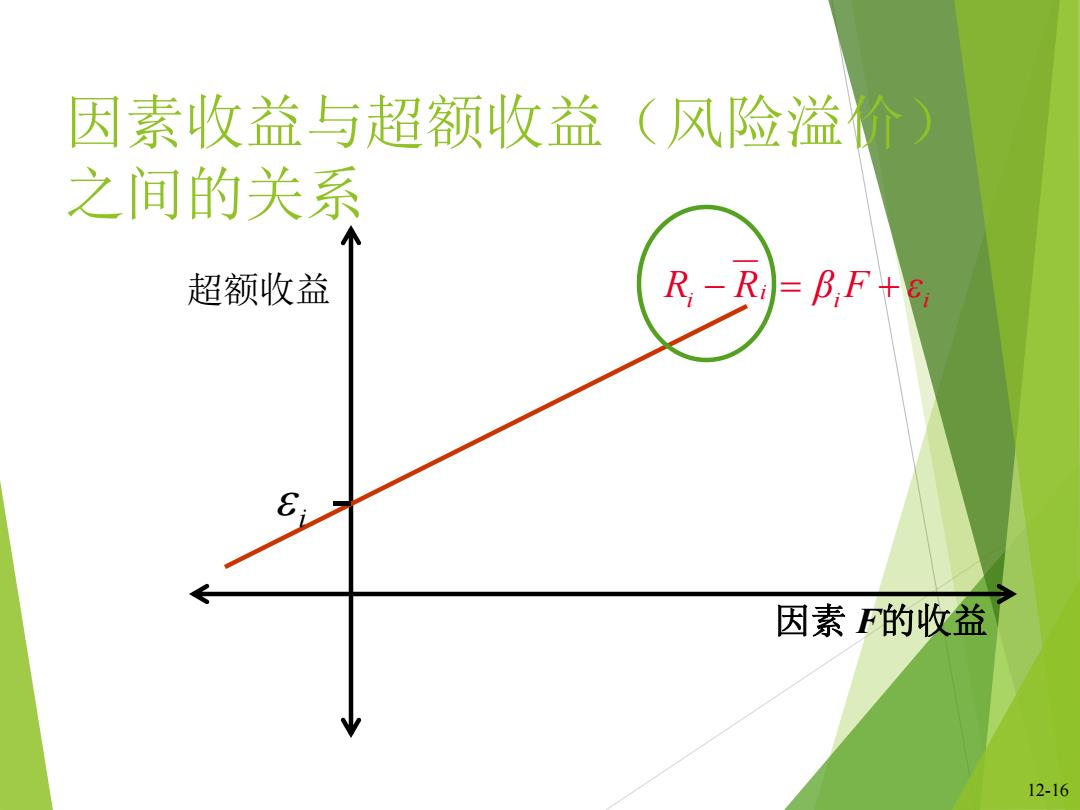
因素收益与超额收益(风险溢价) 之间的关系 超额收益 R-R=BF+e 因素F的收益 12-16
12-16 因素收益与超额收益(风险溢价) 之间的关系 超额收益 因素 F的收益 i i i i i R R β F ε

因素收益与超额收益之间的关系 超额收益 假定没有非系 R-Ri=BF 统性风险,则 6=0。 因素F的收益 12-17
12-17 因素收益与超额收益之间的关系 超额收益 因素 F的收益 假定没有非系 统性风险,则 i = 0。 Ri Ri βiF

因素收益与超额收益之间的关系 超额收益 B4=1.5pg=1.0 不同证券的贝 塔系数是不同 P=0.50的 因素F的收益 12-18
12-18 因素收益与超额收益之间的关系 超额收益 因素 F的收益 不同证券的贝 塔系数是不同 的。 βB 1.0 βC 0.50 βA 1.5

投资组合与多元化 我们知道,投资组合的收益是组合中个别资产收 益的加权平均值: R,=XR+X,R++X③+XwRN R.=Ri+B,F+8 Rp=X (RI+BF+8)+X2(R2+B2F+82)+ ...+Xx(RN+BNF+8N) Rp =X Ri+XB F+X e+X2R2+X2B2F+X262+ …+XNRN+XNBNF+XNGN 12-19
12-19 投资组合与多元化 我们知道,投资组合的收益是组合中个别资产收 益的加权平均值: RP X1R1 X2R2 XiRi X N RN ( ) ( ) ( ) 2 2 2 1 1 2 1 1 N N N N P X R β F ε R X R β F ε X R β F ε N N N N N N P X R X β F X ε R X R X β F X ε X R X β F X ε 2 2 2 2 2 1 1 1 1 2 1 1 i i i i R R β F ε

投资组合与多元化 任何组合的收益都由以下三类参数决定: 1.各种证券期望收益的加权平均值 2.各种证券贝塔系数的加权平均值与因素F的乘积 3.非系统性风险的加权平均值 Rp=XR1+X2R2+…+XN RN +(XB,+X2B2+…+XwBw)F >+X1G+X2E2+…+XNEN 在大型投资组合中,由于非系统性风险基本上都被 分散了,因此上式中的第3项就不存在了。 12-20
12-20 投资组合与多元化 任何组合的收益都由以下三类参数决定: 在大型投资组合中,由于非系统性风险基本上都被 分散了,因此上式中的第3项就不存在了。 N RP X1R1 X2 R2 X N R 1. 各种证券期望收益的加权平均值 (X1 β1 X2 β2 X N βN )F 2. 各种证券贝塔系数的加权平均值与因素F的乘积 N N X ε X ε X ε 1 1 2 2 3. 非系统性风险的加权平均值