
2.算法的描述 0 杜算风利学与技本学脑 ■伪代码 口伪代码是自然语言和类编程语言组成的混合结构, 它比自然语言更精确,更简洁,如果熟悉一门现代 编程语言就更容易理解了。 欧几里得算法的伪代码: 1.r=m%n∥%是求余数运算符 2.while r<>=0∥<>代表不等于 /这条语句的功能是当不等于0的前提下循环下面三行代码 m=n n=r r=m %n 3.输出n
2.算法的描述 ◼ 伪代码 ❑ 伪代码是自然语言和类编程语言组成的混合结构, 它比自然语言更精确,更简洁,如果熟悉一门现代 编程语言就更容易理解了。 欧几里得算法的伪代码: 1. r= m % n //%是求余数运算符 2. while r<>=0 //<>代表不等于 //这条语句的功能是当r不等于0的前提下循环下面三行代码 m=n n=r r=m % n 3. 输出n
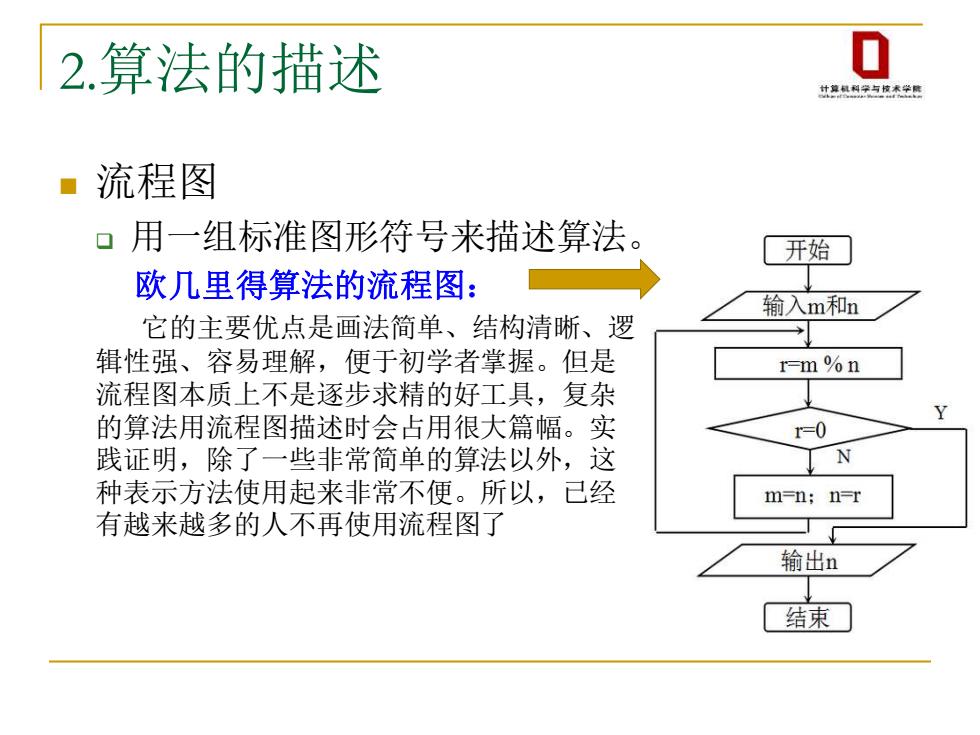
2.算法的描述 0 计草机利学与校术学网 流程图 ▣用一组标准图形符号来描述算法。 开始 欧几里得算法的流程图: 输入m和n 它的主要优点是画法简单、结构清晰、逻 辑性强、容易理解,便于初学者掌握。但是 r=m%n 流程图本质上不是逐步求精的好工具,复杂 Y 的算法用流程图描述时会占用很大篇幅。实 =0 践证明,除了一些非常简单的算法以外,这 种表示方法使用起来非常不便。所以,己经 m=n;n=r 有越来越多的人不再使用流程图了 输出n 结束
2.算法的描述 ◼ 流程图 ❑ 用一组标准图形符号来描述算法。 欧几里得算法的流程图: 它的主要优点是画法简单、结构清晰、逻 辑性强、容易理解,便于初学者掌握。但是 流程图本质上不是逐步求精的好工具,复杂 的算法用流程图描述时会占用很大篇幅。实 践证明,除了一些非常简单的算法以外,这 种表示方法使用起来非常不便。所以,已经 有越来越多的人不再使用流程图了

3.经典算法设计 0 杜算风利学与技本学脑 ·穷举法 口穷举法,也被称为枚举法,是指从可能的集合中一 一枚举各个元素,用题目给定的约束条件判定哪些 是无用的,哪些是有用的,能使命题成立者即为问 题的解。 1)百元百鸡: 公元5世纪末,我国古代数学家张丘建在他编写的《算经》中提 出这样一个问题:“鸡翁一值钱五;鸡母一值钱三;鸡雏三值钱一。 百钱买百鸡,问鸡翁、母、雏各几何?”意思是说,公鸡每只5元, 母鸡每只3元,3只小鸡1元,用100元钱买100只鸡,求公鸡、母鸡和 小鸡各多少只。这里设每种鸡至少一只
3.经典算法设计 ◼ 穷举法 ❑ 穷举法,也被称为枚举法,是指从可能的集合中一 一枚举各个元素,用题目给定的约束条件判定哪些 是无用的,哪些是有用的,能使命题成立者即为问 题的解。 1)百元百鸡: 公元5世纪末,我国古代数学家张丘建在他编写的《算经》中提 出这样一个问题:“鸡翁一值钱五;鸡母一值钱三;鸡雏三值钱一。 百钱买百鸡,问鸡翁、母、雏各几何?”意思是说,公鸡每只5元, 母鸡每只3元,3只小鸡1元,用100元钱买100只鸡,求公鸡、母鸡和 小鸡各多少只。这里设每种鸡至少一只

3.经典算法设计 计草机利学与校未学网 1)百元百鸡: 这个算法对x、y、z都从1开始枚举到100,计算 【算法分析】 机需要做100*100*100次比较操作,虽然这点 我们假达 鸡总数(+y “规模”对计算机来说不算什么,可以很快完成 条件,穷举出计算,但是,这个算法仍然后很大的改进空间。 算法9.2: for1to100/公鸡数从1枚举到100 fory=1to100/母鸡数从1枚举到100 forz=1to100/小鸡数从1枚举到100 if(x+y+z)=100and(5*x+3*y+z/3)=100则 输出x、y、z的值
3.经典算法设计 1)百元百鸡: 【算法分析】 我们假设公鸡、母鸡、小鸡的只数分别为x、y、z。我们以三种 鸡总数(x+y+z)和买鸡的总钱数(5*x+3*y+z/3)都等于100为判定 条件,穷举出各种鸡的只数。 算法9.2: for x=1 to 100 //公鸡数从1枚举到100 for y=1 to 100 //母鸡数从1枚举到100 for z=1 to 100 //小鸡数从1枚举到100 if (x+y+z)=100 and (5*x+3*y+z/3)=100 则 输出x、y、z的值 这个算法对x、y、z都从1开始枚举到100,计算 机需要做100*100*100次比较操作,虽然这点 “规模”对计算机来说不算什么,可以很快完成 计算,但是,这个算法仍然后很大的改进空间

3经典算法设计 杜算风利学与技本学脑 1)百元百鸡: 因为公鸡5元钱一只,所以100元最多买20只公鸡。同理,100元 最多买33只母鸡,而小鸡的数目是100-xy,因此没必要枚举。改进 后的算法如下: 算法9.3: forx=1to20/公鸡数从1枚举到100 fory=1to33/母鸡数从1枚举到100 z=100-×-y if(5*x+3*y+z3)=100则 输出x、y、z的值 改进后的算法让计算机执行操作的次数减少到大约660次。这个 程度的优化在实际运行中是感觉不到的。但是算法优化的思想还请读 者记在心里
3.经典算法设计 1)百元百鸡: 因为公鸡5元钱一只,所以100元最多买20只公鸡。同理,100元 最多买33只母鸡,而小鸡的数目是100-x-y,因此没必要枚举。改进 后的算法如下: 算法9.3: for x=1 to 20 //公鸡数从1枚举到100 for y=1 to 33 //母鸡数从1枚举到100 z=100-x-y if (5*x+3*y+z/3)=100 则 输出x、y、z的值 改进后的算法让计算机执行操作的次数减少到大约660次。这个 程度的优化在实际运行中是感觉不到的。但是算法优化的思想还请读 者记在心里