
第一节应力状态软性系数 这样,在确定的坐标系中描述一个点的 应力状态,可用与坐标轴平行的小六面体上 的应力来表示。共9个应力分量,三个正应 力,六个剪应力(如图2-1所示)。 6
6 第 一 节 应力状态软性系数 这样,在确定的坐标系中描述一个点的 应力状态,可用与坐标轴平行的小六面体上 的应力来表示。共9个应力分量,三个正应 力,六个剪应力(如图2-1所示)
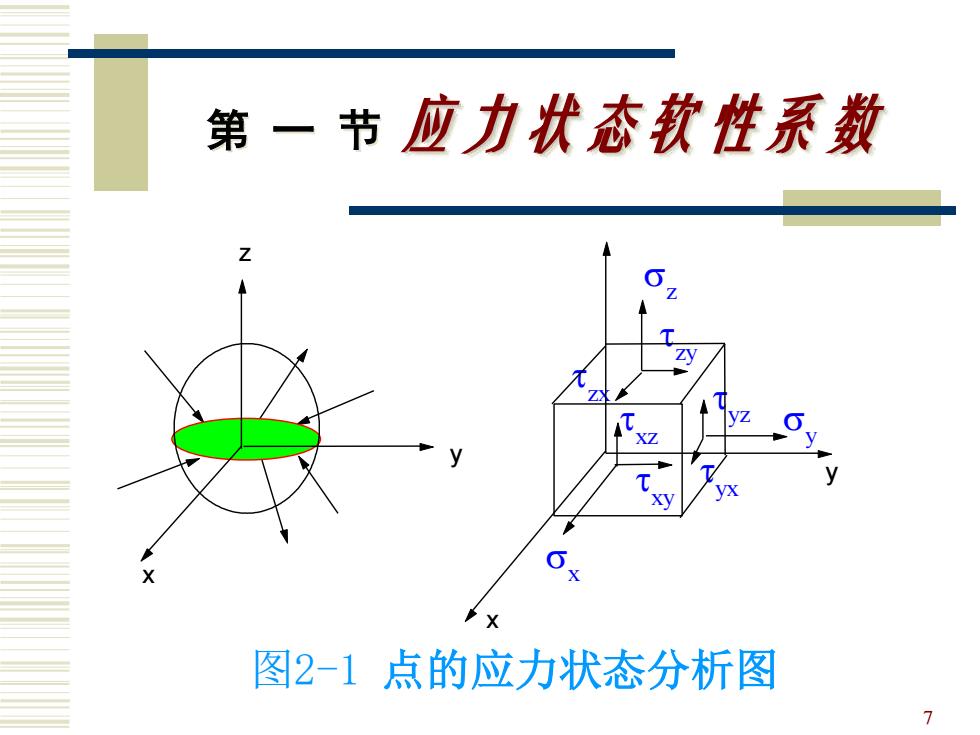
第一节应力状态软性系数 图2-1点的应力状态分析图 7
7 第 一 节 应力状态软性系数 0 2 图2-41 点的应力状态分析图 6 8 10 0 2 4 6 8 10 yx yz y xz xy x zx zy z z y x z y x X Title Y Title ###

第一节应力状态软性系数 Ox,oy,o:一三个正应力,垂直于截面; Tx,x,t,Tx, 六个切应力, 平行于截面,产生塑性变形。 由绕z轴的力距计算: (t·A正·Ay)Ax=(tx·Ax·△)A 可得:t=tyT)=TxTx=Tx 8
8 第 一 节 应力状态软性系数 ——三个正应力,垂直于截面; ——六个切应力, 平行于截面,产生塑性变形。 由绕z轴的力距计算: 可得: x y z , , xy xz yx yz z x z y , , , , , z y x x z y ( xy ) = ( yx ) xy yx = yz zy = xz zx =

第一节应力状态软性系数 上述计算结果表明,点的应力状态只要6 个应力分量就可以描述了。有6个应力分量 就对应有6个应变分量,三个正应变,三个 切应变。 Ox,Oy,0一正应力;Tw,tx,t一切应力: £x,Ey,8:一正应变;Y,Yx,Y一切应变: 9
9 第 一 节 应力状态软性系数 上述计算结果表明,点的应力状态只要6 个应力分量就可以描述了。有6个应力分量 就对应有6个应变分量,三个正应变,三个 切应变。 x y z , , xy xz yz , , x y z , , xy xz yz , , —正应力; —切应力; —正应变; —切应变;

第一节应力状态软性系数 二、三向应力状态下应力一应变 的关系(广义虎克定律) 单向应力状态的虎克定律:。 o-ES 在三向应力状态下,Ox除了在x方向产 生应变外,还在y,z方向产生横向收缩应 】 变,6y=82=-VEx=-V x E (负号表示收缩,V为泊松比) 10
10 第 一 节 应力状态软性系数 二、三向应力状态下应力-应变 的关系(广义虎克定律) 单向应力状态的虎克定律: G E = = x x E x y z x = = − = − 在三向应力状态下, 除了在 x 方向产 生应变 外,还在y, z方向产生横向收缩应 变, (负号表示收缩, 为泊松比)