
衡常数K只决定于反应本性和温度,而与总压及平衡组成无关。气相反应中组分 的逸度 f,=:单,=by:单 (1-35) 式中,为逸度因子(Fugacity factor),其值与反应本性、温度、压力和平衡组成有 关,编制计算机程序时,应采用合适的状态方程计算逸度因子。 等压下Kr与温度的关系可用Van't Hoff方程表示如下: (1-36) 由上式可见,对于吸热反应,4H>0,(2),>0,即K,随温度的升高面增大: 对于做热反应,△P<0,(的),<0,即K,随显度的降低面增大。 式(1-36)在基准温度298.15K与任何温度T间积分,可得K,与温度的关系式、基准 温度下InK,298.15K可由各反应组分的基准温度下的标准摩尔反应吉布斯函数△,G28.15K计算 而得。 对于非理想气体,应用适当的状态方程计算各反应组分的逸度因子值,然后求得同一温 度下的K。值。如果反应体系可作理想气体,则K。=K。一般有关化学产品工业生产的工 艺书籍对低压下许多重要气相反应的平衡常数K,与温度的关系式均有记载。 2.操作参数对产物平衡组成的影响 同一温度但不同压力的K。值随气体混合物偏离理想气体状况的程度而异,压力越高, 温度越低,偏离越大,则压力对K。值的影响也越大。 (p”)(中:) 令K一,K,形式上与平衡常数K,相同,但并非平衡常数,它是气相 反应物系的特性,并且依赖于温度和系统总压p,当反应气体混合物呈非理想气体性质时, 还与平衡组成有关。由式(1-35),可知 (f)(f)M ()() (1-37) 当∑<0,K。及产物的平衡摩尔分数随压力增加而增大产物的平衡摩尔分数随初始 气体混合物中情性物质摩尔分数诚少而增大。 【例14】氨合成反应的平衡常数及平衡组成。 解由于高压下进行氨合成反应的NHH2-N:混合气不仅严重地偏离理想气体的性 质,并且还是非理想溶液,各反应组分的逸度因子不但与温度压力有关,并且与组成有关。 经研究,氨合成反应以逸度表示的平衡常数Ky仅与温度有关,可采用Gillespie及Beattie 发表的方程计算,即 K-/A.).s=exp(-2.691221T+4608.8543/T-1.2708577×10-1T+ 4.257164×10-1P+6.1937237),atm-1 (例1-4-1) 高压下氨合成反应的NH,H2-N2系统是非理想混合物,必须计入压力、温度和混合气 体组成对各组分逸度因子克的影响,可用Beattie-Bridgeman状态方程Io计算
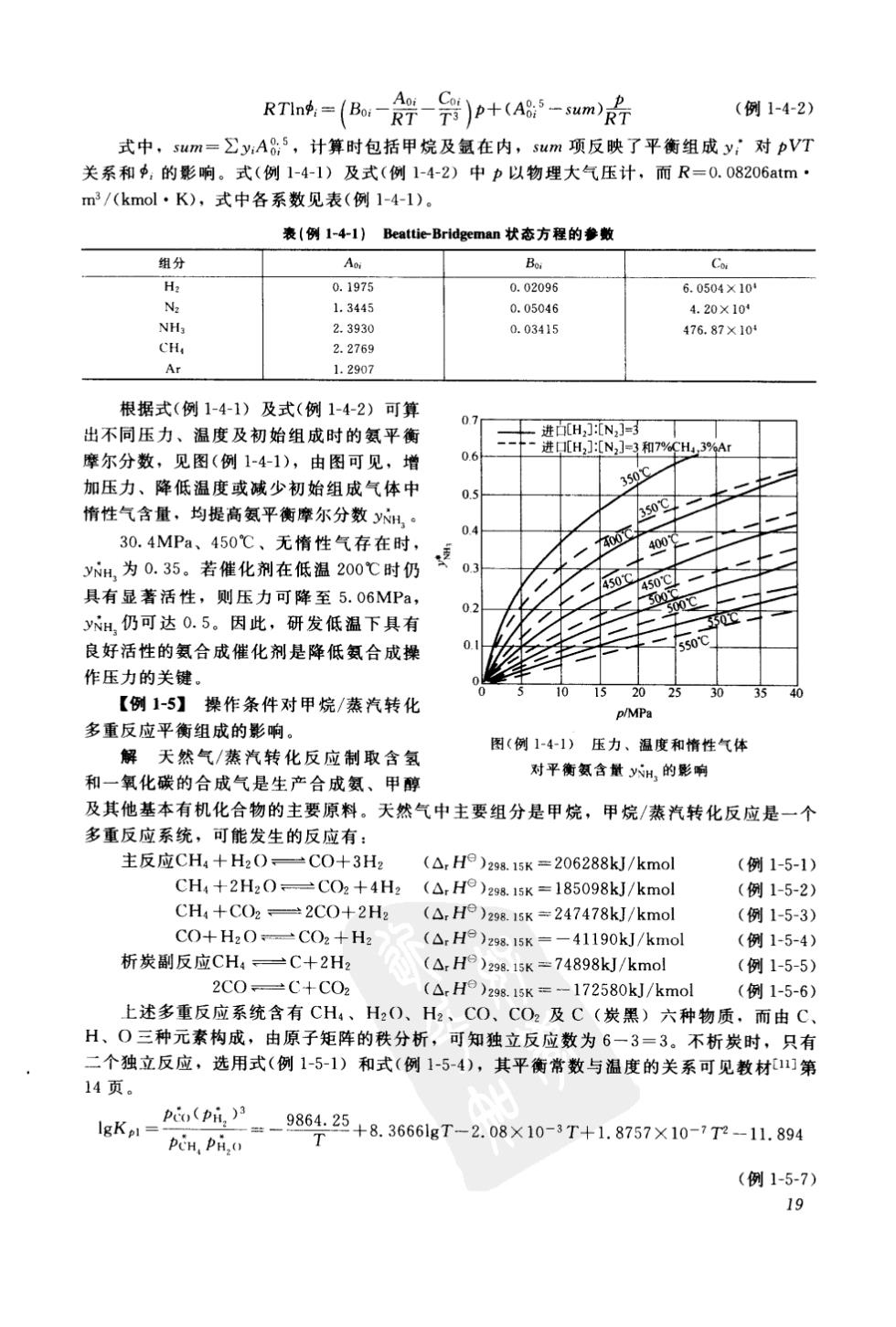
RTnn成=(B,尝-9)p+(A85-wm)号 (例1-42》 式中,swm=∑y:A85,计算时包括甲烷及氯在内,sum项反映了平衡组成y,对pVT 关系和中,的影响。式(例1-4-1)及式(例1-4-2)中p以物理大气压计,而R=0.08206atm· m/(kmol·K),式中各系数见表(例1-4-1).。 表(例1-41)BeatticBridgeman状态方程的参数 组行 A。 0.1975 6. L.34A5 0.05046 2.3930 0.03415 476.87×10 CH 2.2769 Ar 1.2907 根据式(例1-4-1)及式(例1-4-2)可算 出不同压力 温度及初始组成时的氨平衡 摩尔分数,见图(例1-4-1),由图可见,增 6 加压力、降低温度或减少初始组成气体中 r 惰性气含量,均提高氨平衡摩尔分数y 0+ 30.4MPa、450℃、无惰性气存在时, y为0.35。若催化剂在低温200℃时仍 具有显著活性,则压力可降至5.06MPa. y出,仍可达0.5。因此,研发低温下具有 良好活性的氨合成催化剂是降低氨合成操 作压力的关键 【例1-5】操作条件对甲烷/蒸汽转化 多重反应平衡组成的影响 图(例141)压力、温度和惰性气体 解天然气/蒸汽转化反应制取含氢 和一氧化碳的合成气是生产合成氨、甲醇 对平衡氨含献yH的影响 及其他基本有机化合物的主要原料。天然气中主要组分是甲烷,甲烷/蒸汽转化反应是一个 多重反应系统,可能发生的反应有: 主反应CH,+H2O C0+3H (△,HP)29.15K=206288kJ/kmol (例1-5-1) CH,+2H20CO2+4H2 (A.H)29815k=185098kl/kmol (例1-5-2) CH4+C()2,2C0+2H2 (△,H9)29.15K=247478kJ/kmol (例1-5-3) C0+H2O一CO2+H (A.H9 )z9815K=-41190kJ/kmol (例1-5-4 析炭副反应CH =C+2H2 ()238.isK=74898kJ/kmol (例1-5-5) 2C0 L十2 (△.H9)298.15K=-172580kJ/kmol (例1-5-6) 上述多重反应系统含有CH、H2O、H2、CO、CO2及C(炭黑)六种物质,而由C H、0三种元素构成,由原子矩阵的秩分析,可知独立反应数为6一3=3。不析炭时, 只有 二个独立反应,选用式(例1-5-1) 和式(例1-5-4),其平衡常数与温度的关系可见教材第 14页 p,(pi)户 Pen,Pi,o =-986425+8.3661gT-2.08×10-3T+1.8757×10-T-1.894 (例1-5-7) 19
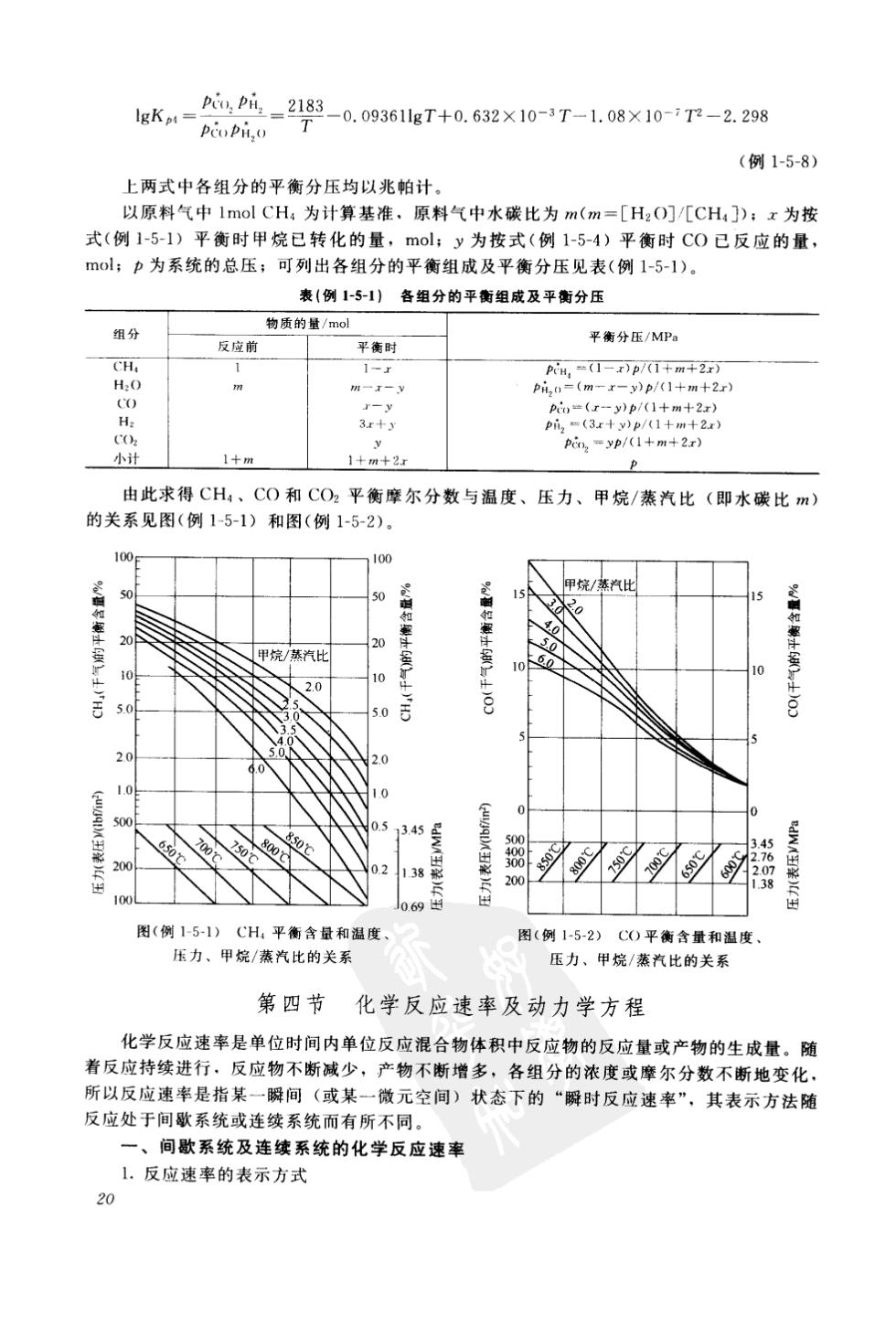
lgK=心L-2183-0.09361lgT+0.632×10-3T-1.08×10-7T-2.298 (例1-5-8) 上两式中各组分的平衡分压均以兆帕计 以原料气中1 mol CH,为计算基准,原料气中水碳比为m(m=[H2O]/[CH:]):x为按 式(例1-5-1)平衡时甲烷已转化的量,mol:y为按式(例1-5-4)平衡时C0已反应的量, molp为系统的总压;可列出各组分的平衡组成及平衡分压见表(例1-5-1) 表(例1-51)各组分的平衡组成及平衡分压 组分 物质的量/mo 反应前 平衡分压/MPa 平衔时 H0 一- 小计 1+m+2x 由此求得CH、CO和CO2平衡摩尔分数与温度、压力、甲烷/蒸汽比(即水碳比m) 的关系见图(例1-5-1)和图(例1-5-2). 10 烧/基汽 5 甲 汽比 0 50 图(例15-1)CH,平衡含量和温度 图(例1-5-2)C0平衡含量和温度 压力、甲烧/蒸汽比的关系 压力、甲烷/蒸汽比的关系 第四节化学反应速率及动力学方程 化学反应速率是单位时间内单位反应混合物体积中反应物的反应量或产物的生成量。随 着反应持续进行、反应物不断减少,产物不断增多,各组分的浓度或摩尔分数不断地变化 所以反应速率是指某一瞬间(或某一微元空间)状态下的“瞬时反应速率 ”,其表示方法随 反应处于间歌系统或连缕系统而有所不同。 一、间歇系统及连续系统的化学反应速率 1.反应速率的表示方式 20

间歇系统中,反应速率表示为单位反应时间内单位反应混合物体积中反应物A的反应 量,而反应时间t为计时器所显示的时间,即 (FA)v-x HA (1-38) 式中,V为釜式反应器中反应混合物所占的体积:nA为某一瞬时反应物A的量,mol: :为反应时间。式中的负号表示反应物A的量随反应时间增加而减少。对于液相均相、液 液非均相反应,反应混合物体积均指液相在釜式反应器中所占的体积:对于气液相或气-液 固三相反应,反应混合物体积均指不含气相的液相或液-固相所古的体积 间歌釜式反应器主要用于液相或以液相占反应器中大部分体积的反应,在此情况下,反 应过程中液相反应混合物体积的变化可以略去,即作等容处理。因此,经典的化学动力学常 以单位时间内反应物或产物的浓度变化来表示反应速率,即 (,)v=士g (1-39 对于反应 VAA十gB=ML十MM (1-40) 各组分的反应速率与化学计量数之间存在着下列关系 (1-41) 连续系统中反应速率可表示为单位反应体积dVR中、或单位反应表面积dS上、或单位 质量固体、或单位质量催化剂W上某一反应物或产物的摩尔流量的变化,即 w=士器度=士器我w=士8 (1-42) 式(1-39)及式(1-42)中,当组分1为反应物时,等号右边均取负值;当i为产物时,均取 正值 式中,N:为组分i的摩尔流量:VR为反应体积。对于均相反应,反应体积是反应混合 物在反应器中所占据的体积;对于气固相催化或非催化反应,反应体积是反应器中颗粒床 层的体积,它包括颗粒的体积和颗粒之间的空隙体积。下标V、S及W分别表示反应床层 体积、反应表面积及固体催化剂质量。 反应体积与固相质量及反应表面积之间可按下式换算: ds=Sdw=S (dVR)=SidVR 1-43) 式中,A为反应体积中固相的堆密度,t/m3床层或kg/L床层,S。为单位质量催化剂 的内表面积(对于多孔催化剂),m2/kg:S为单位床层体积中催化剂的内表面积,m2/m 床层。 在气-固相催化反应的研究中,由于实验反应器与工业反应器中催化剂的堆密度不同, 按单位质量催化剂计算实验室反应器中的反应速率便于换算到工业反应器中的反应速率, 2.空间速度 空间速度(简称空速)(Space Velocity),以符号SV表示,是单位反应体积所能处理 的反应混合物的体积流量,当反应混合物进人及离开反应器的组成处于定值时。空间速度愈 大,表明反应器的空时产率(Space Time Yield,STY)愈大。对于不同性质的反应混合物 体积流量的表示方式不同,例如,反应混合物以液体状态进入反应器,常以25℃下液体的 体积流量表示空速,称为液空速。如果气体混合物含有水蒸气,称为湿空速;不计水蒸气 时,称干空速。 21

反应过程中,气体混合物体积流量随操作状态(压力、温度)而变化,∑≠0的反应 混合物的摩尔流量也有变化。因此,采用不含产物的反应混合物初态组成和STP状况来计 算初态体积流量,以V∞表示。对于循环过程,如氨合成,初态体积流量即将混合气体中全 部氨分解为氢及氮的状态,又称为“氨分解基”体积流量。V在定态连续反应器中不同位 置处不随操作压力、温度和反应进度而变 对于串连的连续流动多级反应器,不以某一级反应器的进口状态计算空速,而以STP 状况下初态的气相反应混合物体积流量来计算空间速度。按单位反应体积计算空速时,气体 混合物的初态体积流量V0以m(STP)/h计,而反应体积VR常以m3计,即空间速度SV 的单位常用h-l。 SV=Vs/VR (1-44) 按单位质量催化剂或固体计算空速,称为质量空速,以符号MSV表示,其单位常以 m3(STP)/(t·h)或L(STP)/(kg·h)表示。催化床中催化剂的堆密度或反应体积中固相 的堆密度为A,则W=VRA,即 MSV=SV/p (1-45) 空间速度SV的倒数定义为标准接触时间to,即为反应体积VR与STP状况初态反应混 合物体积流量V之比,即 o=1/SV=VR/Vso (1-46) V取与进口压力、温度下初态反应混合物体积流量V。之比,称为接触时间t,即 x=Vg/V。 (1-47 停留时间分布的测定是在流体不存在温度及组成变化的等容情况下进行,此时平均停留 时间m可按反应体积VR和等容状况下反应混合物的体积流量V。来计算,即 m=VgV。 (1-48 连续流动反应器中等容过程的平均停留时间m,即接触时间。但对于变容过程,即使 所有质点的停留时间都相同,即平推流,但反应器内物料的实际体积流量V却随反应进度 和温度、压力而变,不能简单地用平均停留时间tm-VRV。来计算。但可采用接触时间t VR,因为V。是进口压力、温度下初态反应混合物体积流量,其值不随反应器中反应进 度、压力和温度的变化而变。 国外有的反应工程教材,如教材[2.l3定义t=VR/W。为“空间时间”(Space time),国 内有的教材简称它为“空时” 对于连续系统,按反应物转化率xA的定义 A=(NA0-NA)/NA0 (1-49) 式中,NA为初态组成(或分解基组成)反应物A的摩尔流量;NA为反应物A的瞬时 摩尔流量,由式(I-49)可知,NA=NAn(I-xA),而dNA=一Naodra,以此代入连续系统 反应物A的反应速率表达式rA=一dNA/dVR,可得以转化率为变量的反应速率表示式如下 rA=/dVR (1-50) 由于dVR=Vso dro,而STP状况下反应物A的初始浓度ca即NAo/Vs,则式(1-50) 可写 rA =chodrA/dto (1-51) 3.反应物的消耗速率和产物的生成速率 对于单一反应,由于转化的反应物全部转化生成产物,在代入化学计量关系后,反应物 的消耗速率可以转化成产物的生成速率。例如,对于反应3H2十N2一一2NH,由于rH,/3 22