电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第六章 线性振动的近似计算方法

R(p)= a'ΦKΦva_mAa a'ΦMΦu =∑ajo 即：o≤R(p)≤o i=1 由瑞利商公式知，当0=确为第一阶模态时，有：R(p)=⊙2 因此，瑞利商的极小值为0 同理可证明，瑞利商的极大值为 如果p接近第k阶真实模态中) 比起ak,其它系数a,很小 aj=ε，akj=1,2,…,n,j≠k8 ,<1 代入，得： oa成+立a-Why?

2 1 由瑞利商公式知，当 确为第一阶模态时，有： R()  φ(1)   因此，瑞利商的极小值为 2 1 同理可证明，瑞利商的极大值为 2 n 如果  接近第k 阶真实模态 φ(k ) a a j n j k j   j k，  1,2,, ,  比起 ak，其它系数ai很小  1 j  代入，得：     n j R k j k j 1 2 2 2 2 ()  (  )        n j j n j T j j T N T N T N T N T R a a 1 2 1 2 2 ()  a Ia a Λa a Φ MΦ a a Φ KΦ a 即： 2 2 1 ( )   R   n

二、瑞利法 R(p)=∑ a a Ro)w+∑(o-oi)s i= 解释： 例如k=1aj=8,a,j=2,…,n R(p)= ao+ao+…+ao 2 a+a+…+a a+a+…+ea 约去a1 +5@++ 2 2 ) 2 1+2+…+8 分子上加减1项 02+5o+…+e7o+(5o2+o2+…+eo)-(e3o+@2+…+eo) 1+8号+…+6 0++…+s）+cio-ai）=8+ i=2 +63+…+E2 1++…+8 ≈02+∑(o-o)

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 1 3 1 1 2 1 3 1 1 2 2 2 1 ( ) ( ) n n n n n                                       分子上加减1项 aj jak       n j R k j k j 1 2 2 2 2 ()  (  ) 解释： 例如 k＝1 a a j n j j 2, ,   1，   2 2 2 2 1 2 2 2 2 2 2 2 1 2 1 ( ) n n n a a a a a a R                   n j j n j R aj j a 1 2 1 2 2 ()  2 2 2 2 2 1 2 2 2 2 2 2 1 1 (1 ) ( ) n n i n i i                     2 2 2 2 2 1 2 2 2 1 1 ( ) n n i i i               2 2 2 2 1 1 2 ( ) n i i i         2 2 2 2 2 2 2 2 2 2 1 1 n n n                 2 1 2 2 1 2 2 2 1 2 2 1 2 2 2 2 1 2 2 2 1 2 1 a a a a a a n n n                 约去a1

二、瑞利法 以此类推，可得 R(o)≈o+∑(o-o)s 因此，若p与)的差异为一阶小量，则瑞利商与⊙的差别为二阶小量。 对于基频的特殊情况，令k=1,则由于o-o2>0(j=2~n) 瑞利商在基频处取极小值. 利用瑞利商估计系统的基频所得的结果必为实际基频的上限 )愈接近系统的真实模态，算出的固有频率愈准确

    n j R k j k j 1 2 2 2 2 ()  (  ) 因此，若  与φ(k )的差异为一阶小量，则瑞利商与 的差别为二阶小量。 2 k 对于基频的特殊情况，令k＝1，则由于 瑞利商在基频处取极小值. 0( 2 ~ ) 2 1 2  j   j  n 利用瑞利商估计系统的基频所得的结果必为实际基频的上限  愈接近系统的真实模态，算出的固有频率愈准确。 以此类推，可得

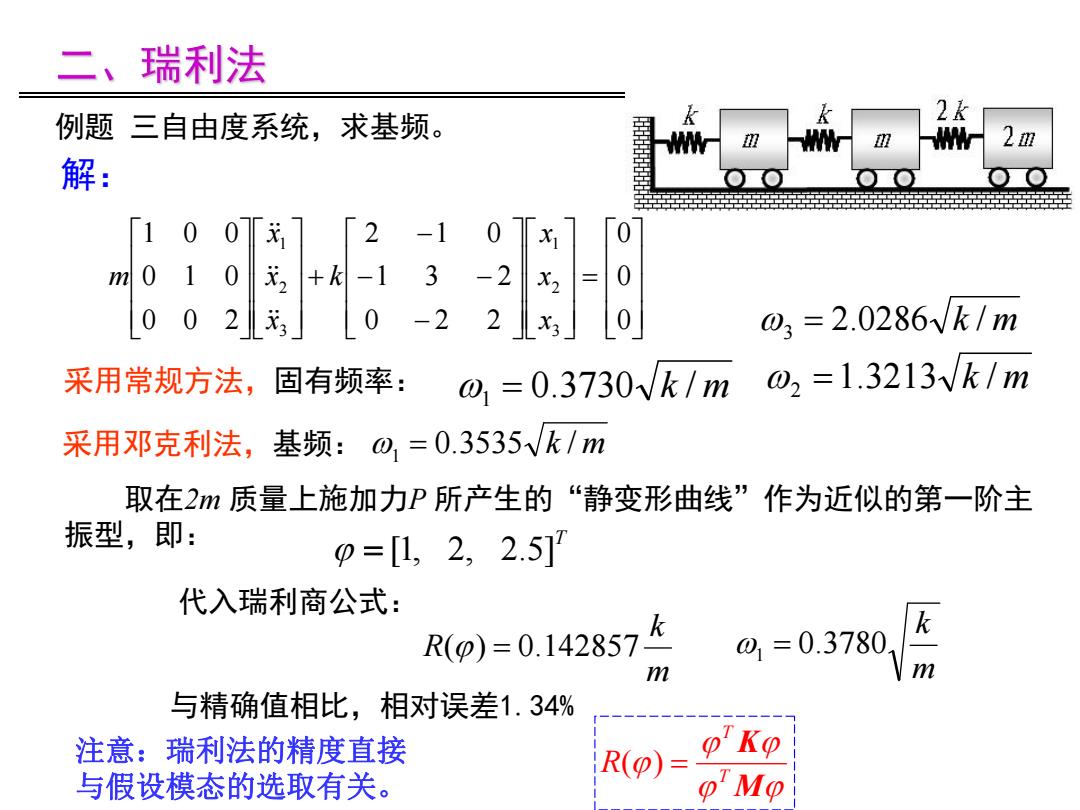
二、瑞利法 例题三自由度系统，求基频。 2m 解： 10 0[龙 「2 -10 0 1 0 +k -1 3 -2 X2 0 o 02 0 -2 2 X3 0 03=2.0286Vk/m 采用常规方法，固有频率： 01=0.3730√k/m o2=1.3213/k/m 采用邓克利法，基频：o,=0.3535Vk/m 取在2m质量上施加力P所产生的“静变形曲线”作为近似的第一阶主 振型，即： 0=[1,2,2.51 代入瑞利商公式： k R(p)=0.142857 m @=0.37801 与精确值相比，相对误差1.34% 注意：瑞利法的精度直接 R(p)= o"Ko 与假设模态的选取有关。 o'Mo

采用邓克利法，基频： 1  0.3535 k / m 取在2m 质量上施加力P 所产生的“静变形曲线”作为近似的第一阶主 振型，即： T   [1, 2, 2.5]      M K T T R( )  代入瑞利商公式： m k R()  0.142857 m k 1  0.3780 与精确值相比，相对误差1.34%                                     0 0 0 0 2 2 1 3 2 2 1 0 0 0 2 0 1 0 1 0 0 3 2 1 3 2 1 x x x k x x x m    采用常规方法，固有频率： 1  0.3730 k / m 2 1.3213 k / m 3  2.0286 k / m 例题 三自由度系统，求基频。 解： 注意：瑞利法的精度直接 与假设模态的选取有关

二、瑞利法 跨座式轨道梁横向自振频率的简化计算方法周小苏

跨座式轨道梁横向自振频率的简化计算方法_周小苏