
-10 第四讲点对称操作 垂直于它的C2轴组合,在垂直于C2轴的平面内必有n个C2轴,相邻两个轴间的夹 角为2r/2n。 (2)两个镜面的组合 两个交角为2x/2n的镜面,其交线必为n次轴。反之,Cn轴和通过该轴并与它平 行的镜面组合,一定存在n个镜面,且相邻镜面的夹角为2π/2m。 (3)偶次旋转轴、镜面和对称中心之间的组合 一个偶次旋转轴与一个垂直于它的镜面组合,必定在交点上出现对称中心;一个偶 次旋转轴与对称中心组合,必有一垂直于这个轴的镜面:对称中心与一镜面组合,必有 一垂直于该面的二次旋转轴
− 10 − 第四讲 点对称操作 垂直于它的 C2 轴组合,在垂直于 C2 轴的平面内必有 n 个 C2 轴,相邻两个轴间的夹 角为 2π/2n。 (2)两个镜面的组合 两个交角为 2π/2n 的镜面,其交线必为 n 次轴。反之,Cn 轴和通过该轴并与它平 行的镜面组合,一定存在 n 个镜面,且相邻镜面的夹角为 2π/2n。 (3)偶次旋转轴、镜面和对称中心之间的组合 一个偶次旋转轴与一个垂直于它的镜面组合,必定在交点上出现对称中心;一个偶 次旋转轴与对称中心组合,必有一垂直于这个轴的镜面;对称中心与一镜面组合,必有 一垂直于该面的二次旋转轴

第五讲 群论基础 1.群(group) 若对称操作A,B,C,·的集合G={A,B,C,.}同时满足以下四个条件,则 G形成一个群。 (1)封闭性:A,B∈G,则C=AB∈G; (2)主操作:G中必有一个E使AE=EA=A: (3)逆操作:HA必有AA-1=A-1A=E; (4)结合律:A(BC)=(AB)C。 2.群的阶:群中包含的元素个数。 3.群的乘法表 群的阶次和群的乘法表大小相同,即n阶群的乘法表的大小必为n×n。根据对 称操作对应矩阵的行列式可以把操作分成两类,行列式为+1的称为第一类操作,如旋 转;行列式为一1的称为第二类操作,如镜面和反演。第一类与第一类、第二类与第二 类的乘积为第一类操作,第一类与第二类的乘积为第二类操作。注意写乘法表时的先后 顺序,先操作行坐标,再操作列坐标。 表5.1C3的乘法表 0 Cg
第五讲 群论基础 1. 群(group) 若对称操作 A, B, C, · · · 的集合 G = {A, B, C, · · · } 同时满足以下四个条件,则 G 形成一个群。 (1)封闭性:A, B ∈ G,则 C = AB ∈ G; (2)主操作:G 中必有一个 E 使 AE = EA = A; (3)逆操作:∀A 必有 AA−1 = A−1A = E; (4)结合律:A(BC) = (AB)C。 2. 群的阶:群中包含的元素个数。 3. 群的乘法表 群的阶次和群的乘法表大小相同,即 n 阶群的乘法表的大小必为 n × n。根据对 称操作对应矩阵的行列式可以把操作分成两类,行列式为 +1 的称为第一类操作,如旋 转;行列式为 −1 的称为第二类操作,如镜面和反演。第一类与第一类、第二类与第二 类的乘积为第一类操作,第一类与第二类的乘积为第二类操作。注意写乘法表时的先后 顺序,先操作行坐标,再操作列坐标。 表 5.1 C3v 的乘法表 C3v E C1 3 C 2 3 σa σb σc E E C1 3 C 2 3 σa σb σc C 1 3 C 1 3 C 2 3 E σc σa σb C 2 3 C 2 3 E C1 3 σb σc σa σa σa σb σc E C1 3 C 2 3 σb σb σc σa C 2 3 E C1 3 σc σc σa σb C 1 3 C 2 3 E
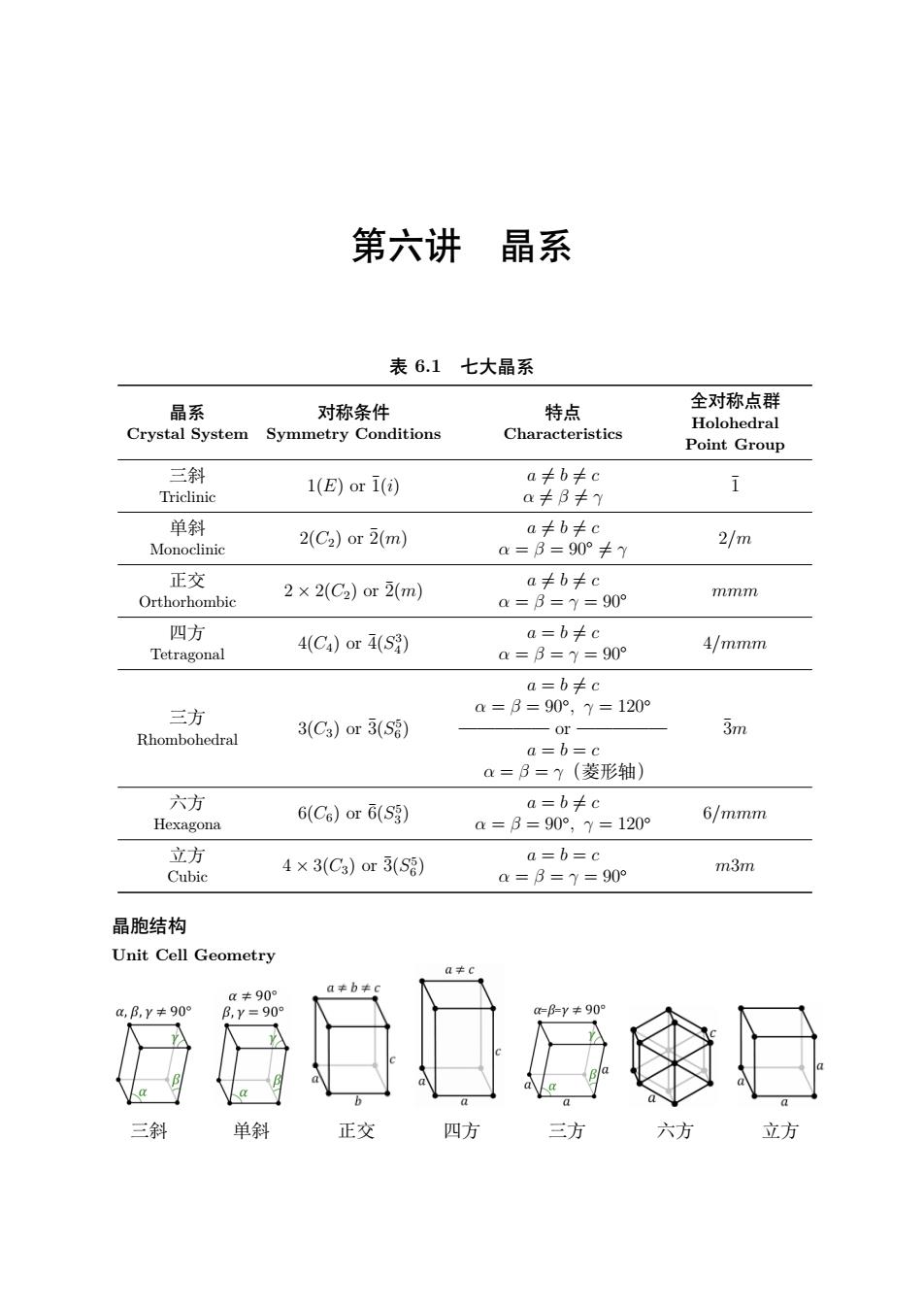
第六讲 晶系 表6.1七大晶系 全对称点群 晶系 对称条件 特点 Crystal System Symmetry Conditions Characteristics Holohedral Point Group 三斜 Triclinic 1(E)or i(i) a≠b≠c a≠B≠y i 2(C2)or2(m) 2/m 正对 a≠b≠c Orthorhombic 2×2(C2)or2(m) a=8=y=90° mmm 四方 Tetragonal 4(C4)or4(S) a=b≠c a=8=1y=90° 4/mmm 三方 Rhombohedral 3(C3)or3(S) 3m 六方 a=b¥c Hexagona 6(C6)or6(S) a=3=90°,y=1209 6/mmm 立方 4×3(C3)or3(Sg) a=b=c Cubic a=B=1=90° m3m 晶胞结构 Unit Cell Geometry 三斜 单斜 正交 四方 六方
第六讲 晶系 表 6.1 七大晶系 晶系 Crystal System 对称条件 Symmetry Conditions 特点 Characteristics 全对称点群 Holohedral Point Group 三斜 Triclinic 1(E) or ¯1(i) a ̸= b ̸= c α ̸= β ̸= γ ¯1 单斜 Monoclinic 2(C2) or ¯2(m) a ̸= b ̸= c α = β = 90◦ ̸= γ 2/m 正交 Orthorhombic 2 × 2(C2) or 2(¯ m) a ̸= b ̸= c α = β = γ = 90◦ mmm 四方 Tetragonal 4(C4) or ¯4(S 3 4 ) a = b ̸= c α = β = γ = 90◦ 4/mmm 三方 Rhombohedral 3(C3) or ¯3(S 5 6 ) a = b ̸= c α = β = 90◦ , γ = 120◦ ————— or ————— a = b = c α = β = γ(菱形轴) ¯3m 六方 Hexagona 6(C6) or ¯6(S 5 3 ) a = b ̸= c α = β = 90◦ , γ = 120◦ 6/mmm 立方 Cubic 4 × 3(C3) or ¯3(S 5 6 ) a = b = c α = β = γ = 90◦ m3m 晶胞结构 Unit Cell Geometry 三斜 单斜 正交 四方 三方 六方 立方
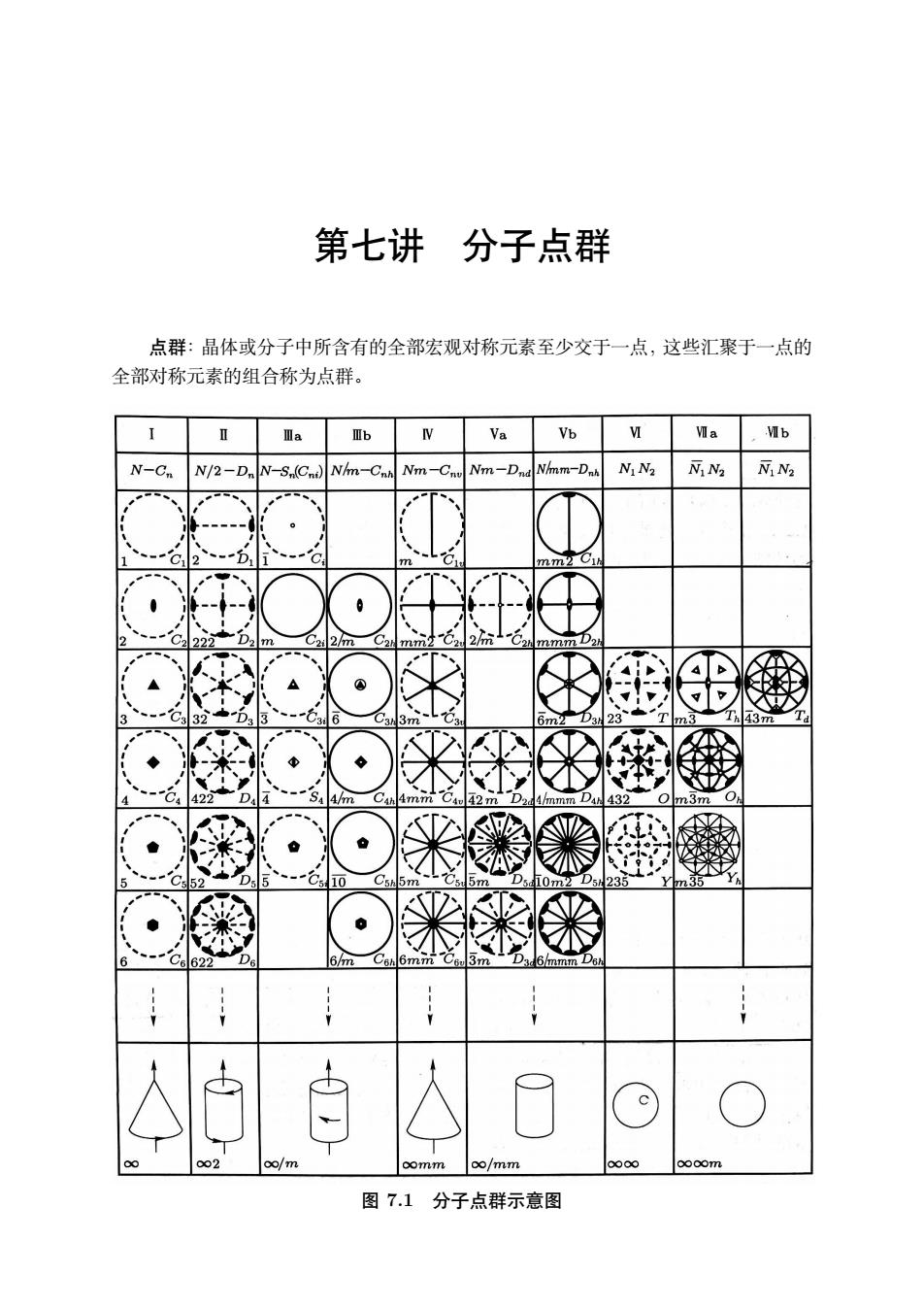
第七讲分子点群 点群:晶体或分子中所含有的全部宏观对称元素至少交于一点,这些汇聚于一点的 全部对称元素的组合称为点群。 Ⅲa Va Vb M Wa Mb N-C. N/2-D.N-S.(Cn)Nhn-Ch Nn CNm-D Nim-D N Na N Na 少$矮 迷出米楼翘 。 迷 comm co/mm 图71分子点群示意图
第七讲 分子点群 点群:晶体或分子中所含有的全部宏观对称元素至少交于一点,这些汇聚于一点的 全部对称元素的组合称为点群。 图 7.1 分子点群示意图