
第三讲 晶体投影 1.意义 (1)投影是研究晶体外形和结构的有用工具。 (2)极射赤面投影能清楚地表达晶体点群中对称要素的空间分布。 2.面角守恒定律:在相同温度和相同压力下,成分上和构造上均相同的同种晶体,其对 应晶面之间的夹角是守恒的 3.球面投影 (1)以晶体的中心为球心,任意合适长度为半径,作一个大圆球面包围整个晶体, 称为参考球或极球: (2)由球心引各个晶面的法线,对应每一晶面的一条发现和参考球相交一点,称为 极点; (3)任意二面角可以直接通过过该二晶面极点的大圆来度量。 4.极射赤面投影(stereographic projection) 以赤道平面为投影面,以南极S(或北极)为视点进行投影,投影面与参考球相 交成赤道大圆,称为基圆。S点和极点P交投影面于P点,即为极点P的极射赤面 投影。可以计算得到 0P=rtan (3.1) 100 1104 -/ 070 110 100 图3.1极射赤面投影 5.极式网和吴式网 极式网是将参考球上经纬线投影到赤道面上得到的图网,吴式网是一组倾斜大圆 和直立小圆投影得到的网图
第三讲 晶体投影 1. 意义 (1)投影是研究晶体外形和结构的有用工具。 (2)极射赤面投影能清楚地表达晶体点群中对称要素的空间分布。 2. 面角守恒定律:在相同温度和相同压力下,成分上和构造上均相同的同种晶体,其对 应晶面之间的夹角是守恒的。 3. 球面投影 (1)以晶体的中心为球心,任意合适长度为半径,作一个大圆球面包围整个晶体, 称为参考球或极球; (2)由球心引各个晶面的法线,对应每一晶面的一条发现和参考球相交一点,称为 极点; (3)任意二面角可以直接通过过该二晶面极点的大圆来度量。 4. 极射赤面投影(stereographic projection) 以赤道平面为投影面,以南极 S(或北极 N)为视点进行投影,投影面与参考球相 交成赤道大圆,称为基圆。S 点和极点 P 交投影面于 P ′ 点,即为极点 P 的极射赤面 投影。可以计算得到 OP′ = r tan α 2 (3.1) 图 3.1 极射赤面投影 5. 极式网和吴式网 极式网是将参考球上经纬线投影到赤道面上得到的图网,吴式网是一组倾斜大圆 和直立小圆投影得到的网图
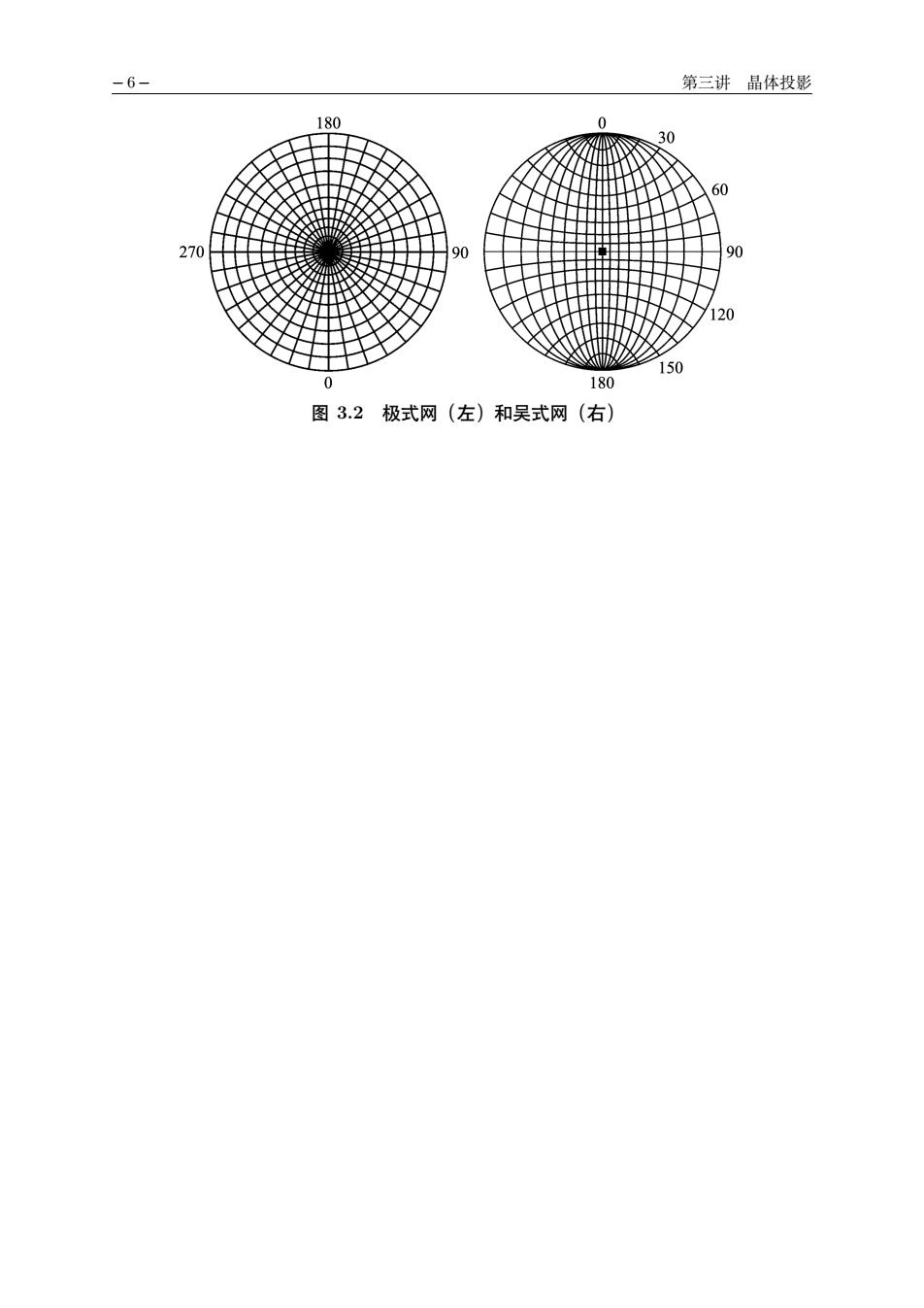
-6 第三讲品体投影 180 120 150 图3.2极式网(左)和吴式网(右)
− 6 − 第三讲 晶体投影 图 3.2 极式网(左)和吴式网(右)

第四讲 点对称操作 1.对称操作和点对称操作 (1)对称操作:对分子或晶体使其各个原子的位置发生变换的操作,结果是使分子 或晶体的状态与操作前的状态相同。 (2)点对称操作:在操作过程中保持空间有一个点不动的对称操作。 2.对称元素和对称操作 表4.1对称元素和对称操作 对称元素符号对称元素基本对称操作符号 基本对称操作 E 恒等操作 旋转轴 绕C.轴逆时针旋转2π/m 对无 S:= 绕S。轴旋转2π/m,接着按垂直于轴的平面反映 n 反轴 n=ic 绕In轴旋转2r/n,接若按中心点反演 (1)旋转轴(Cn)】 旋转操作是将分子或品体绕通过其中心的轴旋转一定角度使分子复原的操作,其 元素为旋转轴,用Cn表示。能使物体复原的最小正旋转角称为基转角(α),Cn轴的 基转角α=2π/n,旋转角度按逆时针方向计算。和Cn轴相应的基本旋转操作为C 当连续进行相同的基本旋转操作时可分别记为 C2=CiC.C8 =CCiCh. (4.1) 所有体系都有无限个C1轴,又称恒等操作或主操作,用E表示,相当于乘法中的1。 对于分子等有限物体,Cm的轴次并不受限,n可以为任意正整数;但在晶体等具有长 程平移对称性的物体,则只有1、2、3、4、6次轴,证明如下。 考虑一个具有n次旋转轴的空间点阵,结点A上有一个基转角为α的旋转轴,根 据点阵的平移性,平移点B点也有一个基转角为α的旋转轴,A点和B点分别以彼 此为轴旋转得到C点和D点,可见AB=AD=BC。根据平移对称性,CD=nAB, 其中n为正整数。由于 CD=AB+2AB cos(-a)=AB(1-2cosa) (4.2) n=1-2c0s0 (4.3) cosa=12E-1,1] 2 (4.4)
第四讲 点对称操作 1. 对称操作和点对称操作 (1)对称操作:对分子或晶体使其各个原子的位置发生变换的操作,结果是使分子 或晶体的状态与操作前的状态相同。 (2)点对称操作:在操作过程中保持空间有一个点不动的对称操作。 2. 对称元素和对称操作 表 4.1 对称元素和对称操作 对称元素符号 对称元素 基本对称操作符号 基本对称操作 E — E 恒等操作 Cn 旋转轴 C1 n 绕 Cn 轴逆时针旋转 2π/n σ 镜面 σ 通过镜面反映 i 对称中心 i 按对称中心反演 Sn 映轴 S 1 n = σC1 n 绕 Sn 轴旋转 2π/n,接着按垂直于轴的平面反映 In 反轴 I 1 n = iC1 n 绕 In 轴旋转 2π/n,接着按中心点反演 (1)旋转轴(Cn) 旋转操作是将分子或晶体绕通过其中心的轴旋转一定角度使分子复原的操作,其 元素为旋转轴,用 Cn 表示。能使物体复原的最小正旋转角称为基转角(α),Cn 轴的 基转角 α = 2π/n,旋转角度按逆时针方向计算。和 Cn 轴相应的基本旋转操作为 C1 n, 当连续进行相同的基本旋转操作时可分别记为 C 2 n = C 1 nC 1 n , C 3 n = C 1 nC 1 nC 1 n , . . . (4.1) 所有体系都有无限个 C1 轴,又称恒等操作或主操作,用 E 表示,相当于乘法中的 1。 对于分子等有限物体,Cn 的轴次并不受限,n 可以为任意正整数;但在晶体等具有长 程平移对称性的物体,则只有 1、2、3、4、6 次轴,证明如下。 考虑一个具有 n 次旋转轴的空间点阵,结点 A 上有一个基转角为 α 的旋转轴,根 据点阵的平移性,平移点 B 点也有一个基转角为 α 的旋转轴,A 点和 B 点分别以彼 此为轴旋转得到 C 点和 D 点,可见 AB = AD = BC。根据平移对称性,CD = nAB, 其中 n 为正整数。由于 CD = AB + 2AB cos(π − α) = AB(1 − 2 cos α) (4.2) n = 1 − 2 cos α (4.3) cos α = 1 − n 2 ∈ [−1, 1] (4.4)

-8 第四讲点对称操作 符合该条件的n=3,2,1,0,-1,对应的a只能为2m,π,2x/3.元/2,π/3,即1、2、3、4、 6次轴。 Oc 图4.1对称定律的证明 在分子和晶体中轴次最高的旋转轴通常被视为主轴,其它旋转轴视为副轴。各种对 称操作都可以用矩阵的形式表示。一般地,C操作可以表示为 cos-sin=0) cosk-sink0 C= sim经cos0 sin2k cos2 0 (4.5) 0 0 0 0 此外,C的逆操作C和C-相等。 (2)镜面(a) 镜面是平分物体的平面,通过反映操作可以复原。反映操作是使分子中的每一点 都反映到该点到镜面垂线的延长线上,在镜面另一侧等距离处。若镜面在xOy平面上, 则。用矩阵可以表示为 -100 (4.6) 连续进行两次反映操作相当于主操作,反映操作和它的逆操作相等。 g”= 了E,n为偶数 (4.7) o,n为奇数 根据镜面和旋转轴的位置关系,镜面共分为三种。与主轴垂直的镜面称为0,通 过主轴的镜面称为σ。,通过主轴且平分垂直于主轴的两个副轴的镜面称为4。通常情 况下,副轴均为C2轴。 图4.2三种镜面
− 8 − 第四讲 点对称操作 符合该条件的 n = 3, 2, 1, 0, −1,对应的 α 只能为 2π, π, 2π/3, π/2, π/3,即 1、2、3、4、 6 次轴。 图 4.1 对称定律的证明 在分子和晶体中轴次最高的旋转轴通常被视为主轴,其它旋转轴视为副轴。各种对 称操作都可以用矩阵的形式表示。一般地,Ck n 操作可以表示为 C k n = cos 2π n − sin 2π n 0 sin 2π n cos 2π n 0 0 0 1 k = cos 2π n k − sin 2π n k 0 sin 2π n k cos 2π n k 0 0 0 1 (4.5) 此外,Ck n 的逆操作 C−k n 和 Cn−k n 相等。 (2)镜面(σ) 镜面是平分物体的平面,通过反映操作可以复原。反映操作是使分子中的每一点 都反映到该点到镜面垂线的延长线上,在镜面另一侧等距离处。若镜面在 xOy 平面上, 则 σ 用矩阵可以表示为 σ = −1 0 0 0 −1 0 0 0 1 (4.6) 连续进行两次反映操作相当于主操作,反映操作和它的逆操作相等。 σ n = E, n为偶数 σ, n为奇数 (4.7) 根据镜面和旋转轴的位置关系,镜面共分为三种。与主轴垂直的镜面称为 σh,通 过主轴的镜面称为 σv,通过主轴且平分垂直于主轴的两个副轴的镜面称为 σd。通常情 况下,副轴均为 C2 轴。 图 4.2 三种镜面

第四讲点对称操作 -9 (3)对称中心() 当物体有对称中心时,从分子中任一原子至对称中心连一直线并延长,必可在和 对称中心等距离的另一侧找到另一相同的原子。和对称中心相应的对称操作称为反演。 若对称中心在原点,反演操作可以表示为 -100 i= 0-10 (4.8) 00-1 连续进行两次反演操作相当于主操作,反演操作和它的逆操作相等。 E,n为偶数 (4.9) i,n为奇数 (4)映轴(Sn) 映轴Sn所对应的基本操作为S,绕Sn轴旋转2r/n,接着按垂直于轴的平面反映, 即S=σC,它是一个联合操作。S1等于镜面,S等于对称中心,S=C3+,S4 是独立的对称元素,S5=C+h,S6=C3+i 对于映轴Sn,当n为奇数时,Sm=Cn+oh,有2n个操作;当n为偶数且不为 4的倍数时,Sn=C/2+i,有n个操作;当n为4的倍数时,Sn是独立的对称元素 且Sm和Cn2同时存在。 图4.3S4操作 (5)反轴(1n】 映轴Sm所对应的基本操作为S绕1n轴旋转2π/m,接着按中心点反演,即 -C,它是一个联合操作。1等于对称中心,2等于镜面,-C3+i-S,4 是独立的对称元素,15=C+i=S10,16=C3+=S3。 对于反轴In,当n为奇数时,In=Cn+i,有n个操作;当n为偶数且不为4的 倍数时,In=Cn/2+o,有n个操作;当n为4的倍数时,In是独立的对称元素,且 In和Cn2同时存在。 3.对称元素的组合 (1)两个旋转轴的组合 交角为2π/2的两个C2轴相组合,在其交点上必定出现一个垂直于这两个C2轴 的Cn轴,而垂直于Cn轴通过交点的平面内必有n个C2轴。反之,由旋转轴Cn与
第四讲 点对称操作 − 9 − (3)对称中心(i) 当物体有对称中心 i 时,从分子中任一原子至对称中心连一直线并延长,必可在和 对称中心等距离的另一侧找到另一相同的原子。和对称中心相应的对称操作称为反演。 若对称中心在原点,反演操作 i 可以表示为 i = −1 0 0 0 −1 0 0 0 −1 (4.8) 连续进行两次反演操作相当于主操作,反演操作和它的逆操作相等。 i n = E, n为偶数 i, n为奇数 (4.9) (4)映轴(Sn) 映轴 Sn 所对应的基本操作为 S 1 n 绕 Sn 轴旋转 2π/n,接着按垂直于轴的平面反映, 即 S 1 n = σC1 n,它是一个联合操作。S1 等于镜面,S2 等于对称中心,S3 = C3 + σh,S4 是独立的对称元素,S5 = C5 + σh,S6 = C3 + i。 对于映轴 Sn,当 n 为奇数时,Sn = Cn + σh,有 2n 个操作;当 n 为偶数且不为 4 的倍数时,Sn = Cn/2 + i,有 n 个操作;当 n 为 4 的倍数时,Sn 是独立的对称元素, 且 Sn 和 Cn/2 同时存在。 图 4.3 S4 操作 (5)反轴(In) 映轴 Sn 所对应的基本操作为 S 1 n 绕 In 轴旋转 2π/n,接着按中心点反演,即 I 1 n = iC1 n,它是一个联合操作。I1 等于对称中心,I2 等于镜面,I3 = C3 + i = S6,I4 是独立的对称元素,I5 = C5 + i = S10,I6 = C3 + σ = S3。 对于反轴 In,当 n 为奇数时,In = Cn + i,有 n 个操作;当 n 为偶数且不为 4 的 倍数时,In = Cn/2 + σ,有 n 个操作;当 n 为 4 的倍数时,In 是独立的对称元素,且 In 和 Cn/2 同时存在。 3. 对称元素的组合 (1)两个旋转轴的组合 交角为 2π/2n 的两个 C2 轴相组合,在其交点上必定出现一个垂直于这两个 C2 轴 的 Cn 轴,而垂直于 Cn 轴通过交点的平面内必有 n 个 C2 轴。反之,由旋转轴 Cn 与