应用:可逆矩阵:分块 算及简单应用:可逆 算:可逆矩阵的求 基本理论模糊不清: 矩阵:矩阵初等变换。 矩阵:分块矩阵:矩 法:矩阵初等变换。 基本计算缺乏演练: 2.掌握n阶行列式的计 阵初等变换。 2.基本掌握n阶行列 基本证明缺乏逻辑。 算方法和技巧:伴随矩 2.较好掌握n阶行列 式的计算方法:伴随 阵求逆。 式的计算方法和技 矩阵求逆。 3.熟练掌握矩阵秩的求 巧:伴随矩阵求逆。 3.基本掌握矩阵秩 法:线性方程组解的判 3.掌握矩阵秩的求 的求法:了解线性方 定。 法:线性方程组解的 程组解的判定。 4.熟练掌握向量组的线 判定。 4.了解向量组的线 性相关性的判断:向量 4.基本掌握向量组 性相关性:基本掌握 组秩的计算:n维向量空 的线性相关性的判 向量组秩的计算:了 间的判断:线性方程组 断:向量组秩的计 解n维向量空间:基 解的表达。 算:n维向量空间的 本掌握线性方程组 5.熟练掌握方阵特征值 判断:线性方程组解 解的表达。 和特征向量的计算方 的表达。 5.基本掌握方阵特 法:实对称矩阵对角化 5.掌握方阵特征值 征值和特征向量的 的条件。 和特征向量的计算 计算方法:了解实对 6.熟练掌握二次型的矩 方法:实对称矩阵对 称矩阵对角化的条 阵表示:化二次型为标 角化的条件。 件。 准形的方法:正定二次 6.掌握二次型的矩 6.基本掌握二次型 型和正定矩阵的判别条 阵表示:化二次型为 的矩阵表示:化二次 件。 标准形的方法:正定 型为标准形的方法: 二次型和正定矩阵 了解正定二次型和 的判别条件。 正定矩阵的判别条 件。 1.熟练掌握矩阵初等变 1.掌握矩阵初等变 1.基本掌握矩阵初 对矩阵的初等变换 换法求解线性方程组。 换法求解线性方程 等变换法求解线性 和基本计算方法掌 2.熟练掌握二次型的矩 组。 方程组。 握不够。 阵表达以及化二次型为 2.掌握二次型的矩 2.基本掌握二次型 标准形的方法: 阵表达以及化二次 的矩阵表达,了解化 课程学习目标2 3.掌握实对称矩阵对角 型为标准形的方法: 二次型为标准形的 化的思想和方法。 3.熟悉实对称矩阵 方法: 对角化的思想和方 3.基本了解实对称 法。 矩阵对角化的思想 和方法。 1.熟练掌握矩阵初等变 1.掌握矩阵初等变 1.基本掌握矩阵初 由于对本课程基本 换。 换。 等变换: 知识了解不够,基本 2.熟练掌握线性方程组 2.掌握线性方程组 2.了解线性方程组 理论掌握不牢,基本 的求解方法。 的求解方法。 的求解步骤: 计算技能欠缺,导致 课程学习目标3 3.熟练掌握方阵特征值 3.会求方阵特征值 3.了解方阵特征值 无法达到课程学习 和特征向量的求法。 和特征向量。 和特征向量的求法。 目标3. 4.熟练掌握正定二次型 4.会判定二次型和 4.了解正定二次型 和正定矩阵判定及应 矩阵是否正定。 和正定矩阵的判定。 用。 19
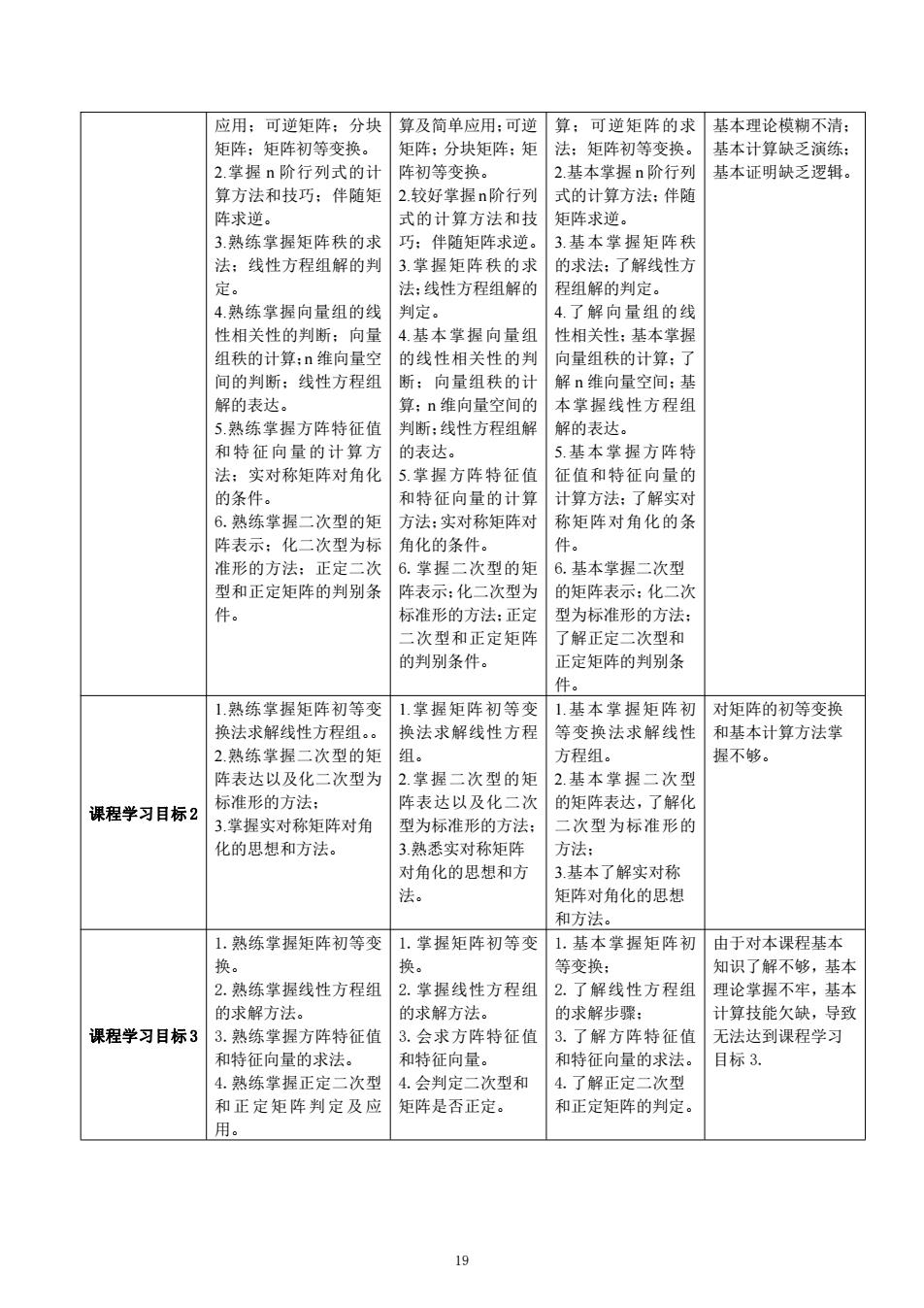
应用;可逆矩阵;分块 矩阵;矩阵初等变换。 2.掌握 n 阶行列式的计 算方法和技巧;伴随矩 阵求逆。 3.熟练掌握矩阵秩的求 法;线性方程组解的判 定。 4.熟练掌握向量组的线 性相关性的判断;向量 组秩的计算;n 维向量空 间的判断;线性方程组 解的表达。 5.熟练掌握方阵特征值 和特征 向量的计 算方 法;实对称矩阵对角化 的条件。 6.熟练掌握二次型的矩 阵表示;化二次型为标 准形的方法;正定二次 型和正定矩阵的判别条 件。 算及简单应用;可逆 矩阵;分块矩阵;矩 阵初等变换。 2.较好掌握n阶行列 式的计算方法和技 巧;伴随矩阵求逆。 3.掌握矩阵秩的求 法;线性方程组解的 判定。 4.基本掌握向量组 的线性相关性的判 断;向量组秩的计 算;n 维向量空间的 判断;线性方程组解 的表达。 5.掌握方阵特征值 和特征向量的计算 方法;实对称矩阵对 角化的条件。 6.掌握二次型的矩 阵表示;化二次型为 标准形的方法;正定 二次型和正定矩阵 的判别条件。 算;可逆矩阵的求 法;矩阵初等变换。 2.基本掌握 n 阶行列 式的计算方法;伴随 矩阵求逆。 3.基本掌握矩阵秩 的求法;了解线性方 程组解的判定。 4.了解向量组的线 性相关性;基本掌握 向量组秩的计算;了 解 n 维向量空间;基 本掌握线性方程组 解的表达。 5.基本掌握方阵特 征值和特征向量的 计算方法;了解实对 称矩阵对角化的条 件。 6.基本掌握二次型 的矩阵表示;化二次 型为标准形的方法; 了解正定二次型和 正定矩阵的判别条 件。 基本理论模糊不清; 基本计算缺乏演练; 基本证明缺乏逻辑。 课程学习目标 2 1.熟练掌握矩阵初等变 换法求解线性方程组。。 2.熟练掌握二次型的矩 阵表达以及化二次型为 标准形的方法; 3.掌握实对称矩阵对角 化的思想和方法。 1.掌握矩阵初等变 换法求解线性方程 组。 2.掌握二次型的矩 阵表达以及化二次 型为标准形的方法; 3.熟悉实对称矩阵 对角化的思想和方 法。 1.基本掌握矩阵初 等变换法求解线性 方程组。 2.基本掌握二次型 的矩阵表达,了解化 二次型为标准形的 方法; 3.基本了解实对称 矩阵对角化的思想 和方法。 对矩阵的初等变换 和基本计算方法掌 握不够。 课程学习目标 3 1.熟练掌握矩阵初等变 换。 2.熟练掌握线性方程组 的求解方法。 3.熟练掌握方阵特征值 和特征向量的求法。 4.熟练掌握正定二次型 和正定 矩阵判定 及应 用。 1.掌握矩阵初等变 换。 2.掌握线性方程组 的求解方法。 3.会求方阵特征值 和特征向量。 4.会判定二次型和 矩阵是否正定。 1.基本掌握矩阵初 等变换; 2.了解线性方程组 的求解步骤; 3.了解方阵特征值 和特征向量的求法。 4.了解正定二次型 和正定矩阵的判定。 由于对本课程基本 知识了解不够,基本 理论掌握不牢,基本 计算技能欠缺,导致 无法达到课程学习 目标 3. 19
《概率论与数理统计》课程教学大纲 一、课程基本信息 课程 课程 5103002 概率论与数理统计 编号 名称 学分/学时 4学分64学时 开课时间 第3学期 课程性质 专业必修课 先修课程 高等数学、线性代数 课程基 考核方式 考试(平时30%、期末考试70%) 本情况 课程负责人 教材:《概率论与数理统计》,同济大学数学系编,人民邮电出版社, 2017年。 参考书目: 教材及 ①《概率论与数理统计》(第四版),盛骤、谢式千、潘承毅编,高 参考书 等教育出版社,2008年: ②《概率论与数理统计教程》(第二版),茆诗松、程依明、濮晓龙 编,高等教育出版社,2011年: 《概率论与数理统计》是计算机科学与技术等理工科专业的专业必修课,主要研 究随机现象的统计规律性,目前己经成为科学、工程、管理等许多学科的重要工具, 在计算机系统、金融、气象设计、地震预测、遗传规律、卫星摄影等方面有重要应用。 课程 本课程主要讲授概率论与数理统计的基本概念、基本理论和基本方法,主要包括 简介 概率论和数理统计分析的理论介绍,概率和条件概率,连续型和离散型随机变量及其 概率分布,一维与多维随机变量的数学期望和方差等数字特征,大数定律与中心极限 定理,参数估计,假设检验等。 学习目标1:了解概率论与数理统计课程的地位与性质,系统掌握概率论与数理统计 的基本概念、基本理论和基本方法。 课程学习 学习目标2:建立必要的概率统计基本知识素养,掌握处理随机现象统计规律的思想 目标 和方法。 学习目标3:运用概率统计方法分析和解决实际不确定问题的基本素质和基本技能。 20
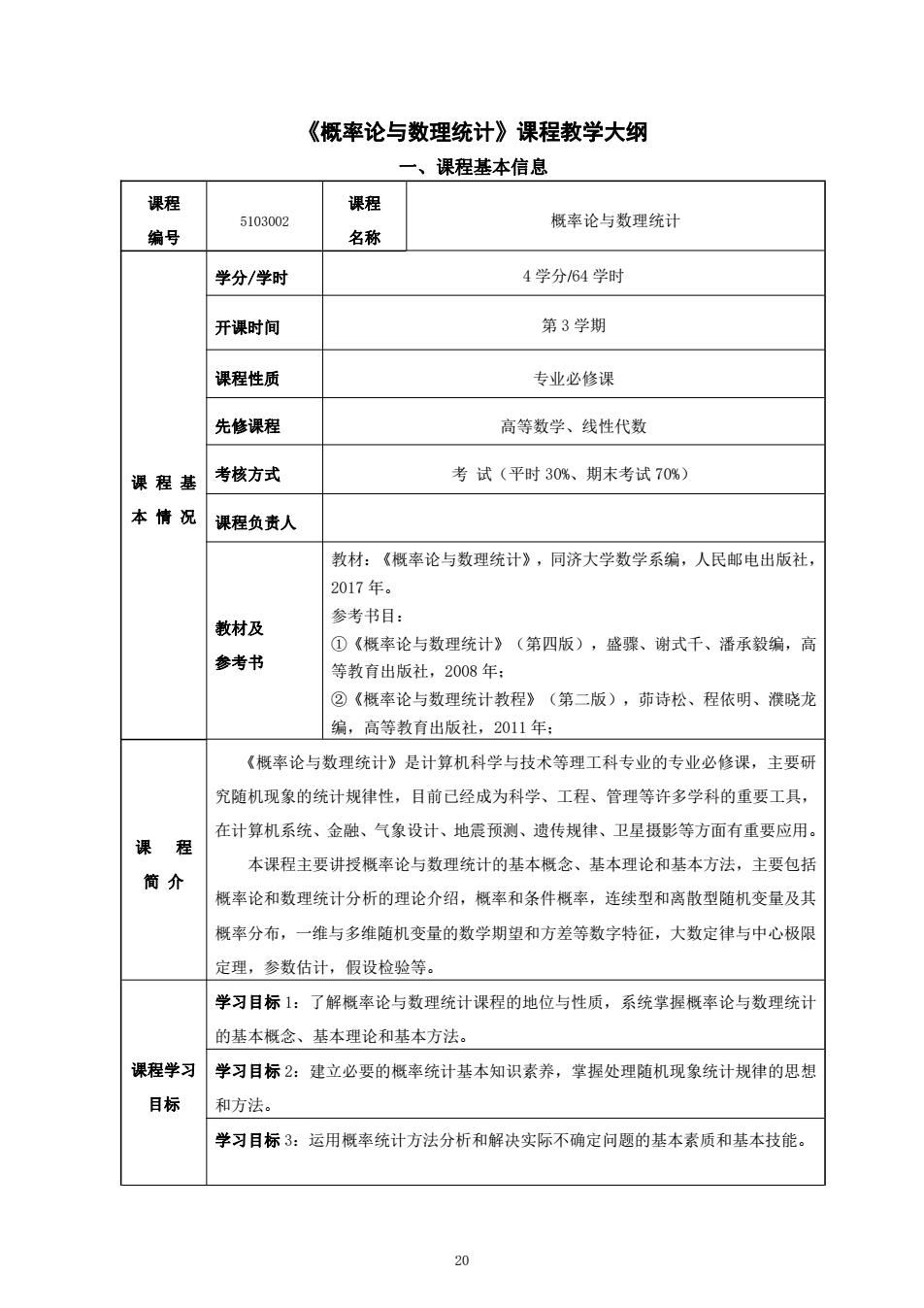
《概率论与数理统计》课程教学大纲 一、课程基本信息 课程 编号 5103002 课程 名称 概率论与数理统计 课 程 基 本 情 况 学分/学时 4 学分/64 学时 开课时间 第 3 学期 课程性质 专业必修课 先修课程 高等数学、线性代数 考核方式 考 试(平时 30%、期末考试 70%) 课程负责人 教材及 参考书 教材:《概率论与数理统计》,同济大学数学系编,人民邮电出版社, 2017 年。 参考书目: ①《概率论与数理统计》(第四版),盛骤、谢式千、潘承毅编,高 等教育出版社,2008 年; ②《概率论与数理统计教程》(第二版),茆诗松、程依明、濮晓龙 编,高等教育出版社,2011 年; 课 程 简 介 《概率论与数理统计》是计算机科学与技术等理工科专业的专业必修课,主要研 究随机现象的统计规律性,目前已经成为科学、工程、管理等许多学科的重要工具, 在计算机系统、金融、气象设计、地震预测、遗传规律、卫星摄影等方面有重要应用。 本课程主要讲授概率论与数理统计的基本概念、基本理论和基本方法,主要包括 概率论和数理统计分析的理论介绍,概率和条件概率,连续型和离散型随机变量及其 概率分布,一维与多维随机变量的数学期望和方差等数字特征,大数定律与中心极限 定理,参数估计,假设检验等。 课程学习 目标 学习目标 1:了解概率论与数理统计课程的地位与性质,系统掌握概率论与数理统计 的基本概念、基本理论和基本方法。 学习目标 2:建立必要的概率统计基本知识素养,掌握处理随机现象统计规律的思想 和方法。 学习目标 3:运用概率统计方法分析和解决实际不确定问题的基本素质和基本技能。 20

二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 了解概率论与数理统计的发展史及其在社会发展中的地 位以及重要作用,了解概率论与数理统计领域的一些最新研究 成果和教学方法;掌握教育学、心理学和计算机科学教育的基 2.3知识整合 本理论,熟悉中小学数学以及教育法规:学习人类文明进步 课程学习目标1、3 与文化发展的通识知识。具有整合数学、教育学、心理学等数 理知识和教育技术并进行知识与技能重构的能力,具有熟练运 用现代计算机及信息教育技术进行教研的能力。 具备良好的计算机学科素养,深入理解并掌握概率论与数 理统计方面的基本理论和方法,并能获得较强的逻辑推理能 力、抽象思维能力和解决随机问题的能力。初步掌握计算机科 2.4教学能力 学学科的基本思想方法,具有利用概率论与数理统计知识解决 课程学习目标1、2、3 实际问题等基本能力:具有较强的独立学习能力和创新思维方 式,懂得教育教学基本规律,掌握现代教育教学、心理学的基 本理论。 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:随机事件与概率(可支撑课程学习目标1、2、3) 1.教学目的和要求 了解随机试验、样本空间的概念:理解随机事件、条件概率、随机事件相互独立概念,古典概型和 几何概型、概率的公理化定义、全概率公式和贝叶斯公式;掌握随机事件的关系和运算、古典概型和几 何概型问题的求解、概率的基本性质、加法公式及减法公式的运用、用事件相互独立性及全概率公式和 贝叶斯公式进行概率计算的方法。 2.教学内容 第1.1节:随机事件及其运算 第1.2节:概率的定义及其性质 第1.3节:等可能概型 第1.4节:条件概率与事件的相互独立性 第15节:全概率公式与贝叶斯公式 21
二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 2.3 知识整合 了解概率论与数理统计的发展史及其在社会发展中的地 位以及重要作用,了解概率论与数理统计领域的一些最新研究 成果和教学方法;掌握教育学、心理学和计算机科学教育的基 本理论,熟悉中小学数学以及教育法规; 学习人类文明进步 与文化发展的通识知识。具有整合数学、教育学、心理学等数 理知识和教育技术并进行知识与技能重构的能力,具有熟练运 用现代计算机及信息教育技术进行教研的能力。 课程学习目标 1、3 2.4 教学能力 具备良好的计算机学科素养,深入理解并掌握概率论与数 理统计方面的基本理论和方法,并能获得较强的逻辑推理能 力、抽象思维能力和解决随机问题的能力。初步掌握计算机科 学学科的基本思想方法,具有利用概率论与数理统计知识解决 实际问题等基本能力;具有较强的独立学习能力和创新思维方 式,懂得教育教学基本规律,掌握现代教育教学、心理学的基 本理论。 课程学习目标 1、2、3 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:随机事件与概率(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 了解随机试验、样本空间的概念;理解随机事件、条件概率、随机事件相互独立概念,古典概型和 几何概型、概率的公理化定义、全概率公式和贝叶斯公式;掌握随机事件的关系和运算、古典概型和几 何概型问题的求解、概率的基本性质、加法公式及减法公式的运用、用事件相互独立性及全概率公式和 贝叶斯公式进行概率计算的方法。 2 . 教学内容 第 1.1 节:随机事件及其运算 第 1.2 节:概率的定义及其性质 第 1.3 节:等可能概型 第 1.4 节:条件概率与事件的相互独立性 第 1.5 节:全概率公式与贝叶斯公式 21

3.教学重点:随机事件的运算、概率的定义及其基本性质、古典概型和几何概型的计算、条件 概率和乘法公式以及全概率公式和贝叶斯公式的应用。 4.教学难点:概率的公理化定义的理解、概率模型的建立、全概率公式和贝叶斯公式在实际问 题中的应用。 5.学时:10学时 第二章随机变量及其分布(可支撑课程学习目标1、2、3) 1.教学目的和要求 理解随机变量的定义、分布律或密度函数与分布函数的关系:掌握随机变量分布函数、离散型随机 变量分布律及连续型随机变量的定义、性质与计算:掌握二项分布、泊松分布、均匀分布、指数分布和 正态分布的概率模型及相关概率问题的求解:掌握一维随机变量函数的分布的求解问题。 2.教学内容 第2.1节:随机变量及其分布 第2.2节:常用的离散型随机变量 第2.3节:常用的连续型随机变量 第2.4节:随机变量函数的分布 3.教学重点:常用的离散型随机变量的概率分布律,常用的连续型随机变量的概率分布。 4.教学难点:一维随机变量的函数的概率分布的计算。 5.学时:10学时 第三章二维随机变量及其分布(可支撑课程学习目标1、2、3) 1.教学目的和要求 理解二维随机变量的概念、二维随机变量的联合分布的概念、性质:理解随机变量的边缘分布及独 立性的概念:掌握离散型和连续型随机变量独立的条件:掌握二维均匀分布,了解二维正态分布的联合 概率密度,理解其中参数的概率意义:会利用二维概率分布求有关事件的概率,会求两个随机变量的简 单函数(和、差、积、商,最大最小值)的分布。 2.教学内容 第3.1节:二维随机变量及其联合分布 第3.2节:常用的二维随机变量 第3.3节:边缘分布 第3.5节:二维随机变量函数的分布 3.教学重点:二维随机变量的联合分布和边缘分布:随机变量的独立性的判断:两个随机变量 和、差、积、商等的分布律或密度函数及分布函数的计算:最大最小值分布的计算。 22
3 . 教学重点:随机事件的运算、概率的定义及其基本性质、古典概型和几何概型的计算、条件 概率和乘法公式以及全概率公式和贝叶斯公式的应用。 4 . 教学难点:概率的公理化定义的理解、概率模型的建立、全概率公式和贝叶斯公式在实际问 题中的应用。 5 . 学时:10 学时 第二章 随机变量及其分布(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 理解随机变量的定义、分布律或密度函数与分布函数的关系;掌握随机变量分布函数、离散型随机 变量分布律及连续型随机变量的定义、性质与计算;掌握二项分布、泊松分布、均匀分布、指数分布和 正态分布的概率模型及相关概率问题的求解;掌握一维随机变量函数的分布的求解问题。 2 . 教学内容 第 2.1 节:随机变量及其分布 第 2.2 节:常用的离散型随机变量 第 2.3 节:常用的连续型随机变量 第 2.4 节:随机变量函数的分布 3 . 教学重点:常用的离散型随机变量的概率分布律,常用的连续型随机变量的概率分布。 4 . 教学难点:一维随机变量的函数的概率分布的计算。 5 . 学时:10 学时 第三章 二维随机变量及其分布(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 理解二维随机变量的概念、二维随机变量的联合分布的概念、性质;理解随机变量的边缘分布及独 立性的概念;掌握离散型和连续型随机变量独立的条件;掌握二维均匀分布,了解二维正态分布的联合 概率密度,理解其中参数的概率意义;会利用二维概率分布求有关事件的概率,会求两个随机变量的简 单函数(和、差、积、商,最大最小值)的分布。 2 . 教学内容 第 3.1 节:二维随机变量及其联合分布 第 3.2 节:常用的二维随机变量 第 3.3 节:边缘分布 第 3.5 节:二维随机变量函数的分布 3 . 教学重点:二维随机变量的联合分布和边缘分布;随机变量的独立性的判断;两个随机变量 和、差、积、商等的分布律或密度函数及分布函数的计算;最大最小值分布的计算。 22

4.教学难点:二维随机变量的边缘分布与独立性的判断:两个随机变量和、差、积、商等的分 布律或密度函数及分布函数的计算:最大最小值分布的计算。 5.学时:10学时 第四章随机变量的数字特征(可支撑课程学习目标1、2) 1.教学目的和要求 理解离散型、连续型随机变量的数学期望、方差、协方差、相关系数的定义及其概率含义及k阶矩 的定义:熟悉数学期望、方差、协方差、相关系数的性质;掌握随机变量及其函数的期望、方差、协方 差、相关系数的计算公式,正态分布的k阶原点矩的计算公式(尤其标准正态分布):熟练常用随机变 量的数学期望、方差的计算:了解期望向量、协方差矩阵的定义及简单计算,变异系数、分位数、中位 数及众数的定义及简单计算。 2.教学内容 第4.1节:数学期望 第4.2节:方差和标准差 第4.3节:协方差和相关系数 第4.4节:其他数字特征 3.教学重点:数学期望和方差的概念、性质与求法,常用随机变量的数学期望与方差、随机变 量函数的数学期望的计算,协方差、相关系数的计算。 4.教学难点:随机变量函数的数学期望的计算。 5.学时:8学时 第五章大数定律及中心极限定理(可支撑课程学习目标1、2) 1.教学目的和要求 理解切比雪夫不等式的意义,依概率收敛的定义,大数定律在实际中的应用:掌握用切比雪夫不等 式求解概率PX-4≥ε)的上界;了解切比雪夫大数定律、伯努利大数定律、辛钦大数定律成立的条 件及结论,了解列维一林德伯格中心定理和棣莫弗一拉普拉斯中心极限定理的应用条件和结论,并会用 相关定理求解相互独立随机变量之和的近似概率值。 2.教学内容 第5.1节:大数定律 第5.2节:中心极限定理 3.教学重点:切比雪夫不等式的应用、大数定律。 4,教学难点:中心极限定理的运用。 5.学时:4学时 23
4 . 教学难点:二维随机变量的边缘分布与独立性的判断;两个随机变量和、差、积、商等的分 布律或密度函数及分布函数的计算;最大最小值分布的计算。 5 . 学时:10 学时 第四章 随机变量的数字特征(可支撑课程学习目标 1、2) 1. 教学目的和要求 理解离散型、连续型随机变量的数学期望、方差、协方差、相关系数的定义及其概率含义及 k 阶矩 的定义;熟悉数学期望、方差、协方差、相关系数的性质;掌握随机变量及其函数的期望、方差、协方 差、相关系数的计算公式,正态分布的 k 阶原点矩的计算公式(尤其标准正态分布);熟练常用随机变 量的数学期望、方差的计算;了解期望向量、协方差矩阵的定义及简单计算,变异系数、分位数、中位 数及众数的定义及简单计算。 2 . 教学内容 第 4.1 节:数学期望 第 4.2 节:方差和标准差 第 4.3 节:协方差和相关系数 第 4.4 节:其他数字特征 3 . 教学重点:数学期望和方差的概念、性质与求法,常用随机变量的数学期望与方差、随机变 量函数的数学期望的计算,协方差、相关系数的计算。 4 . 教学难点:随机变量函数的数学期望的计算 。 5 . 学时:8 学时 第五章 大数定律及中心极限定理(可支撑课程学习目标 1、2) 1 . 教学目的和要求 理解切比雪夫不等式的意义,依概率收敛的定义,大数定律在实际中的应用;掌握用切比雪夫不等 式求解概率 P X( ) 的上界;了解切比雪夫大数定律、伯努利大数定律、辛钦大数定律成立的条 件及结论,了解列维—林德伯格中心定理和棣莫弗—拉普拉斯中心极限定理的应用条件和结论,并会用 相关定理求解相互独立随机变量之和的近似概率值。 2 . 教学内容 第 5.1 节:大数定律 第 5.2 节:中心极限定理 3 . 教学重点:切比雪夫不等式的应用、大数定律。 4 . 教学难点:中心极限定理的运用。 5 . 学时:4 学时 23