
实验一LC串联电路特性的研究 电阻、电容及电感是电路中的基本元件,由C、RL、LC构成的串联电路具有不同 的特性,包括暂态特性、稳态特性、谐振特性.它们在实际应用中都起着重要的作用. 【实验目的】 1.通过研究RC、L和RLC串联电路的暂态过程,加深对电容充、放电规律,电感 的电磁感应特性及振荡回路特点的认识: 2.掌握RC、RL和RLC串联电路的幅频特性和相频特性的测量方法: 3.用实验的方法测量LC电路的谐振频率,利用幅频曲线求出电路的品质因数Q值. 【实验原理】 1.RC、RL、RLC暂态过程 (1)RC串联电路 在由R、C组成的电路中,暂态过程是电容的充放电的过程.图1为RC串联电路.其 中信号源用方波信号.在上半个周期内,方波电压+E,其对电容充电:在下半个周期内, 方波电压为零,电容对地放电.充电过程中的回路方程为 RCUE+Ue=E (1) dt 由初始条件1=0时,Uc=0,得解为 Uc=E(1-e RC) (2) Ug=iR=Ee RC 图1RC串联电路 从Uc、UR二式可见,UC是随时间1按指数函数规律增长,而电阻电压UR随时间1按指 数函数规律衰减,如图2中U-1、Uc-1及UR-1曲线所示. 在放电过程中的回路方程为 Rcd0e+U。=0 (3) dt 由初始条件t=0时,Uc=E,得解为 Ue =Ee (4) UR=iR=-Ee定 从UC、U式可见,它们都随时间1按指数函数规律衰减.式中的RC=x具有时间的量纲, -1-
实验一 RLC 串联电路特性的研究 电阻、电容及电感是电路中的基本元件,由 RC、RL、RLC 构成的串联电路具有不同 的特性,包括暂态特性、稳态特性、谐振特性.它们在实际应用中都起着重要的作用. 【实验目的】 1.通过研究 RC、RL 和 RLC 串联电路的暂态过程,加深对电容充、放电规律,电感 的电磁感应特性及振荡回路特点的认识; 2.掌握 RC、RL 和 RLC 串联电路的幅频特性和相频特性的测量方法; 3.用实验的方法测量 RLC 电路的谐振频率,利用幅频曲线求出电路的品质因数 Q 值. 【实验原理】 1.RC、RL、RLC 暂态过程 (1)RC 串联电路 在由 R、C 组成的电路中,暂态过程是电容的充放电的过程.图 1 为 RC 串联电路.其 中信号源用方波信号.在上半个周期内,方波电压+E,其对电容充电;在下半个周期内, 方波电压为零,电容对地放电.充电过程中的回路方程为 EU t U RC C C =+ d d (1) 图 1 RC 串联电路 由初始条件t = 0 时,UC = 0,得解为 RC t R RC t C EeiRU eEU − − == −= )1( (2) 从UC、UR 二式可见,UC 是随时间 t 按指数函数规律增长,而电阻电压UR 随时间 t 按指 数函数规律衰减,如图2中U – t、UC – t 及UR – t 曲线所示. 在放电过程中的回路方程为 0 d d C =+ C U t U RC (3) 由初始条件t = 0 时,UC = E,得解为 RC t R RC t C EeiRU EeU − − −== = (4) 从UC、UR式可见,它们都随时间 t 按指数函数规律衰减.式中的RC = τ 具有时间的量纲, - 1 -

称为时间常数,是表征暂态过程进行得快慢的一个重 要物理量.与时间常数π有关的另一个在实验中较容 U E 易测定的特征值,称为半衰期T12,即当Uc(t)下降 到初值(或上升至终值)一半时所需要的时间,它同 样反映了暂态过程的快慢程度,与x的关系为 T2=tln2=0.693x(或x=1.443Tn)(5) (2)L串联电路 与RC串联电路进行类似分析可得,RL串联电路 的时间常数r及半衰期Ti2分别为: ,7:=0.693r=0.693 T=L (6) R E (3)RLC串联电路 先讨论LC电路中突然接入电源,电容器上电压 满足的微分方程为 LCUE+RC UE+Uc-E (7) dr2 dt E 等式边同除以LC,并令 图2RC串联电路充放电曲线 B=R/2L0。= (8) VLC 则上式可化为 dU+2BaC+oU。=aE dr2 (9) dt 式(9)为一阻尼振荡方程,B为阻尼系数,o为电路的固有频率.又由本过程的两个初始 条件 Ucl-o=0; =0 (10) dt 所以(10)式最终解的形式取决于B和oo的相对大小. 下面就分三种情况给出结果 (1)欠阻尼 当B2-o<0时,称为欠阻尼, 其解为 U=E-Ee cos+sin o (11) -2-
E 0 t UC T E 0 U t T E 0 t UR T -E 图 2 RC 串联电路充放电曲线 称为时间常数,是表征暂态过程进行得快慢的一个重 要物理量.与时间常数τ 有关的另一个在实验中较容 易测定的特征值,称为半衰期T1/2,即当UC(t)下降 到初值(或上升至终值)一半时所需要的时间,它同 样反映了暂态过程的快慢程度,与τ 的关系为 T1/2 = τ ln2 = 0.693 τ (或τ = 1.443T1/2) (5) (2)RL串联电路 与RC 串联电路进行类似分析可得,RL串联电路 的时间常数τ 及半衰期T1/2分别为: R L T R L 693.0693.0 , τ = 2/1 τ == (6) (3)RLC 串联电路 先讨论 RLC 电路中突然接入电源,电容器上电压 满足的微分方程为 EU t U RC t U LC C C C + =+ d d d d 2 2 (7) 等式边同除以 LC,并令 β = 2LR LC 1 ω0 = (8) 则上式可化为 EU t U t U C C C 2 0 2 2 0 2 d d 2 d d =++ ωωβ (9) 式(9)为一阻尼振荡方程,β为阻尼系数,ω 0为电路的固有频率.又由本过程的两个初始 条件 0 0 = C t = U ; 0 d d 0 = t= C t U (10) 所以(10)式最终解的形式取决于β 和ω 0的相对大小. 下面就分三种情况给出结果 (1)欠阻尼 当 2 ωβ 0 2 <− 0 时,称为欠阻尼, 其解为 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= + − ttEeEU t C ω ω β ω β cos sin (11) - 2 -
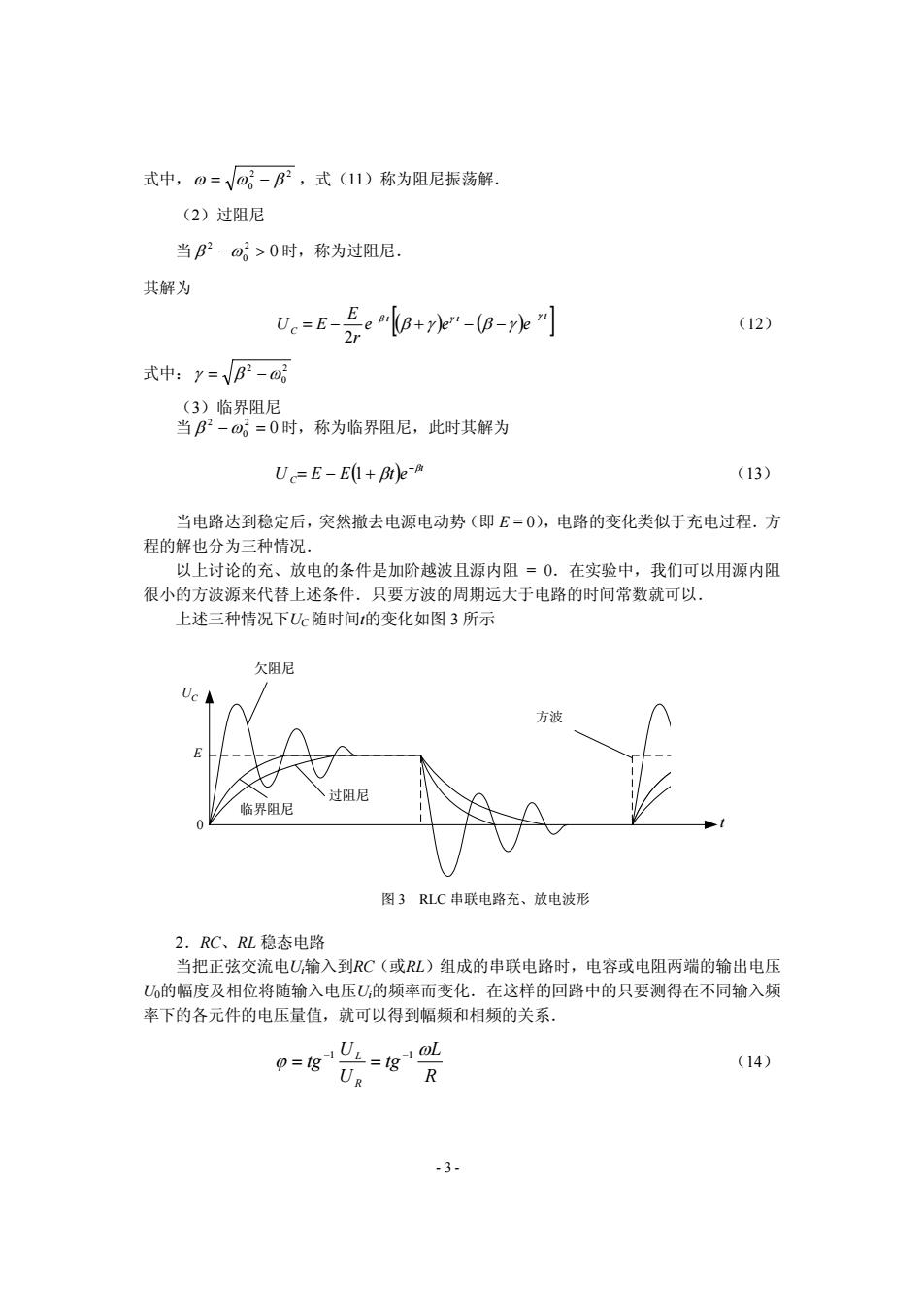
式中,o=√o-B2,式(11)称为阻尼振荡解. (2)过阻尼 当B2-o>0时,称为过阻尼. 其解为 u=E号ela+--h叫 (12) 式中:y=VB2-o6 (3)临界阻尼 当B2-⊙。=0时,称为临界阻尼,此时其解为 UC=E-E(1+Bt)e- (13) 当电路达到稳定后,突然撤去电源电动势(即£=0),电路的变化类似于充电过程.方 程的解也分为三种情况 以上讨论的充、放电的条件是加阶越波且源内阻=0.在实验中,我们可以用源内阻 很小的方波源来代替上述条件.只要方波的周期远大于电路的时间常数就可以. 上述三种情况下Uc随时间的变化如图3所示 欠阻尼 方波 过阻尼 临界阻尼 图3RLC串联电路充、放电波形 2.RC、RL稳态电路 当把正弦交流电U,输入到RC(或L)组成的串联电路时,电容或电阻两端的输出电压 U6的幅度及相位将随输入电压U的频率而变化.在这样的回路中的只要测得在不同输入频 率下的各元件的电压量值,就可以得到幅频和相频的关系, 0-8UL (14) UR R -3-
式中, 22 0 −= βωω ,式(11)称为阻尼振荡解. (2)过阻尼 当 2 ωβ 0 2 >− 0 时,称为过阻尼. 其解为 [( )( ) ]t t t C ee e r E EU 2 γ β γ γβγβ − − −= −−+ (12) 式中: 2 0 2 −= ωβγ (3)临界阻尼 当 2 ωβ 0 2 =− 0 时,称为临界阻尼,此时其解为 ( ) t C etEEU β β − 1+−= (13) 当电路达到稳定后,突然撤去电源电动势(即 E = 0),电路的变化类似于充电过程.方 程的解也分为三种情况. 以上讨论的充、放电的条件是加阶越波且源内阻 = 0.在实验中,我们可以用源内阻 很小的方波源来代替上述条件.只要方波的周期远大于电路的时间常数就可以. 上述三种情况下UC 随时间t的变化如图 3 所示 图 3 RLC 串联电路充、放电波形 0 t UC E 欠阻尼 临界阻尼 过阻尼 方波 2.RC、RL 稳态电路 当把正弦交流电Ui输入到RC(或RL)组成的串联电路时,电容或电阻两端的输出电压 U0的幅度及相位将随输入电压Ui的频率而变化.在这样的回路中的只要测得在不同输入频 率下的各元件的电压量值,就可以得到幅频和相频的关系. R L tg U U tg R L ω ϕ −1 −1 == (14) - 3 -

0=g1C=g(-R (15) 3.RLC谐振电路 UL-Uc 图4RLC串联电路 (1)如图4所示的是RLC串联电路.RLC串联电路的阻抗和相位差可通过矢量图的 方法计算,因为通过各元件的电流是共同的.取电流矢量I为水平基准,又由于各分电压 与电流的相位差为 m,=0,以=受0=号 2 所以各元件的电压有效值为 Ug=IZ IR,U IZ loL,Uc=IZc =1/@C (16) 总电压 U=0+0,-万度U=R+- (17) 电路总阻抗为 Z=1 R2+(@L-- (18) 电流与信号电压的位相差为 p=g二Uc=g l、1 (19) UR R -4-
) 1 ( 1 1 CR tg U U tg R C ω ϕ −= − = − − (15) 3.RLC 谐振电路 图 4 RLC 串联电路 (1)如图 4 所示的是 RLC 串联电路.RLC 串联电路的阻抗和相位差可通过矢量图的 方法计算,因为通过各元件的电流是共同的.取电流矢量 I 为水平基准,又由于各分电压 与电流的相位差为 ϕ R = 0 , 2 π ϕ L = , 2 π ϕc −= 所以各元件的电压有效值为 R == , L = L = ω , C = C = /ωCIIZULIIZUIRIZU (16) 总电压 2 2 )( R −+= UUUU CL 或 2 2 ) 1 ( C LRIU ω ω −+= (17) 电路总阻抗为 2 2 ) 1 ( C LRZ ω ω −+= (18) 电流与信号电压的位相差为 R C L tg U UU tg R CL ω ω ϕ 1 1 1 − = − = − − (19) - 4 -
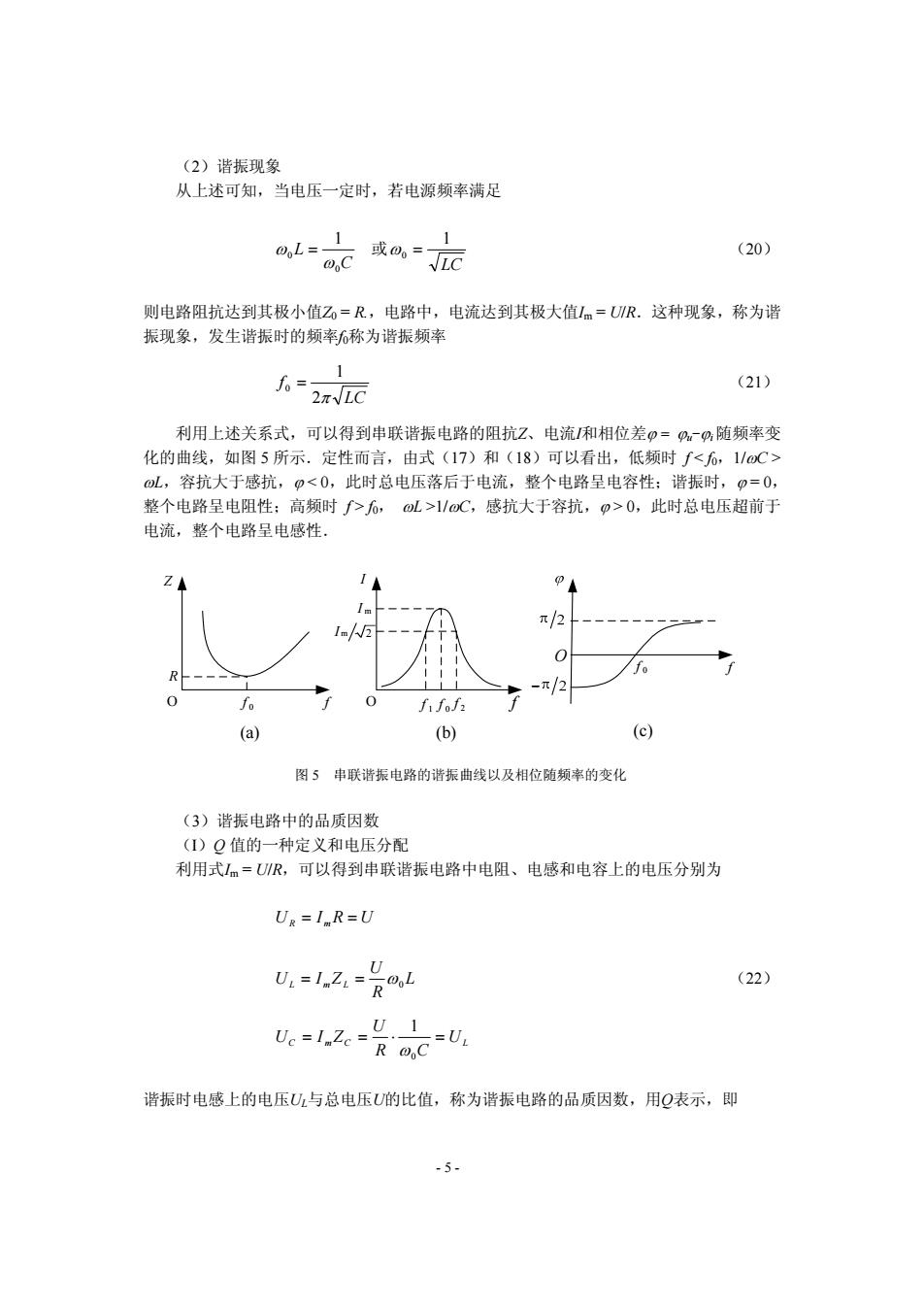
(2)谐振现象 从上述可知,当电压一定时,若电源频率满足 0L= (20) 0C LC 则电路阻抗达到其极小值Zo=R,电路中,电流达到其极大值Im=R.这种现象,称为谐 振现象,发生谐振时的频率6称为谐振频率 1 人=2m0 (21) 利用上述关系式,可以得到串联谐振电路的阻抗Z、电流和相位差p=p,随频率变 化的曲线,如图5所示.定性而言,由式(17)和(18)可以看出,低频时f<f,1/oC> L,容抗大于感抗,p<0,此时总电压落后于电流,整个电路呈电容性:谐振时,p=0, 整个电路呈电阻性:高频时f>6,oL>1/oC,感抗大于容抗,p>0,此时总电压超前于 电流,整个电路呈电感性。 π/2 fo -π/2 10 fifof2 (a) (b) (c) 图5串联谐振电路的谐振曲线以及相位随频率的变化 (3)谐振电路中的品质因数 (I)Q值的一种定义和电压分配 利用式I=UR,可以得到串联谐振电路中电阻、电感和电容上的电压分别为 UR=I R=U U,=1.Z,=R05 (22) Uc=IZe=RO _U1 -=UL 谐振时电感上的电压U与总电压U的比值,称为谐振电路的品质因数,用Q表示,即 -5-
(2)谐振现象 从上述可知,当电压一定时,若电源频率满足 C L 0 0 1 ω ω = 或 LC 1 ω0 = (20) 则电路阻抗达到其极小值Z0 = R.,电路中,电流达到其极大值Im = U/R.这种现象,称为谐 振现象,发生谐振时的频率f0称为谐振频率 LC f 2π 1 0 = (21) 利用上述关系式,可以得到串联谐振电路的阻抗Z、电流I和相位差ϕ = ϕu-ϕi 随频率变 化的曲线,如图 5 所示.定性而言,由式(17)和(18)可以看出,低频时 f < f0,1/ωC > ωL,容抗大于感抗,ϕ < 0,此时总电压落后于电流,整个电路呈电容性;谐振时,ϕ = 0, 整个电路呈电阻性;高频时 f > f0, ωL >1/ωC,感抗大于容抗,ϕ > 0,此时总电压超前于 电流,整个电路呈电感性. O f R Z f 0 f 0 f 1 f 2 O I I m I m 2 f f 0 O f (a) (b) (c) 图 5 串联谐振电路的谐振曲线以及相位随频率的变化 (3)谐振电路中的品质因数 (I)Q 值的一种定义和电压分配 利用式Im = U/R,可以得到串联谐振电路中电阻、电感和电容上的电压分别为 mR == URIU L R U ZIU LmL == ω0 (22) CmC UL CR U ZIU =⋅== 0 1 ω 谐振时电感上的电压UL与总电压U的比值,称为谐振电路的品质因数,用Q表示,即 - 5 -