归本程子末军 3.哈夫曼树和哈夫曼编码 HANDONG UNIVERSITY OF TECINOLOGY 哈夫曼树: 假设有n个权值{w1w2w,构造一颗有n个叶子 结,点的二叉树,每个叶子结点所带权值为“,则 其中WL最小的二叉树称为最优二叉树或哈夫曼 树。其中,WPL的计算公式为: wPL=∑wklk 例如:由w1=1,w2=3,w3=7 组成的哈夫曼树为: 2025/413
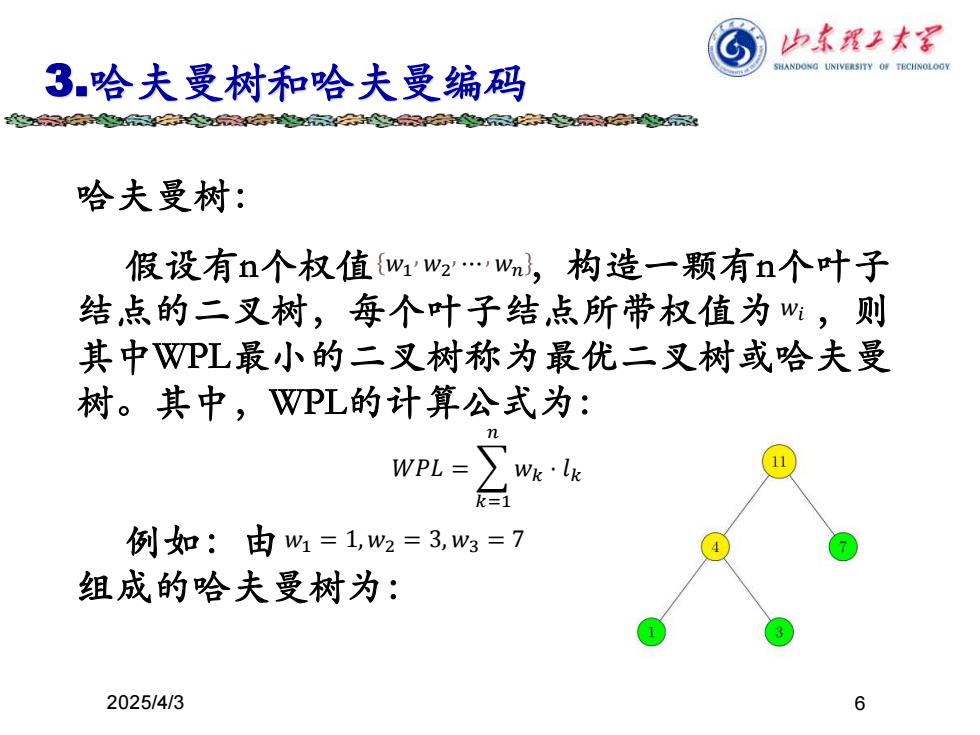
6 3.哈夫曼树和哈夫曼编码 2025/4/3 哈夫曼树: 假设有n个权值 ,构造一颗有n个叶子 结点的二叉树,每个叶子结点所带权值为 ,则 其中WPL最小的二叉树称为最优二叉树或哈夫曼 树。其中,WPL的计算公式为: 𝑊𝑃𝐿 = 𝑘=1 𝑛 𝑤𝑘 ⋅ 𝑙𝑘 𝑤1 𝑤2 ⋯ 𝑤𝑛 𝑤𝑖 例如:由 组成的哈夫曼树为: 𝑤1 = 1, 𝑤2 = 3, 𝑤3 = 7

归本程上太军 3.哈夫曼树和哈夫曼编码 SHANDONG UNIVERSITY OF TECINOLOGY 如何构造哈夫曼树: 1,根据给定的n个权值W'WzWn},构造包含n颗 二叉树的集合F={阳2Tn,其中每颗二叉树中均只 含一个带权值为的根结点,其左、右子树为空树; 2,在F中选取其根结,点的权值最小的两颗二叉树, 分别作为左、右子树构造一个新的二叉树,并置这 颗新的二叉树根节点的权值为其左、右子树根结点 的权值之和; 3,从F中删去这两颗树,同时加入刚生成的新树; 4,重复2和3两步,直至F中只含一颗树为止。 2025/413
7 3.哈夫曼树和哈夫曼编码 如何构造哈夫曼树: 1,根据给定的n个权值 ,构造包含n颗 二叉树的集合 ,其中每颗二叉树中均只 含一个带权值为 的根结点,其左、右子树为空树; 2,在F中选取其根结点的权值最小的两颗二叉树, 分别作为左、右子树构造一个新的二叉树,并置这 颗新的二叉树根节点的权值为其左、右子树根结点 的权值之和; 3,从F中删去这两颗树,同时加入刚生成的新树; 4,重复2和3两步,直至F中只含一颗树为止。 2025/4/3 𝑤1 𝑤2 ⋯ 𝑤𝑛 F = 𝑇1 𝑇2 ⋯ 𝑇𝑛 𝑤𝑖
归东程子太军 HANDONG UNIVERSITY OF TECHNOLOOY 3.哈夫曼树和哈夫曼编码 如果我们规定Iuffman {5,6,2,9,7},构造哈夫 树的左分支编码为0,右分 支编码为1,则字符的编码 0 就是从根到该字符所在的 13 16 叶结点的路径上的分支编 9 号序列,称为Iuffman编码 d 显然这是一 假如字符v={A,B,C,D,E} 个前缀码 的权值分别为 w={5,6,2,9,7}。那么字符v A B E 的Huffman编码结果为: 101 00 100 11 01 2025/413
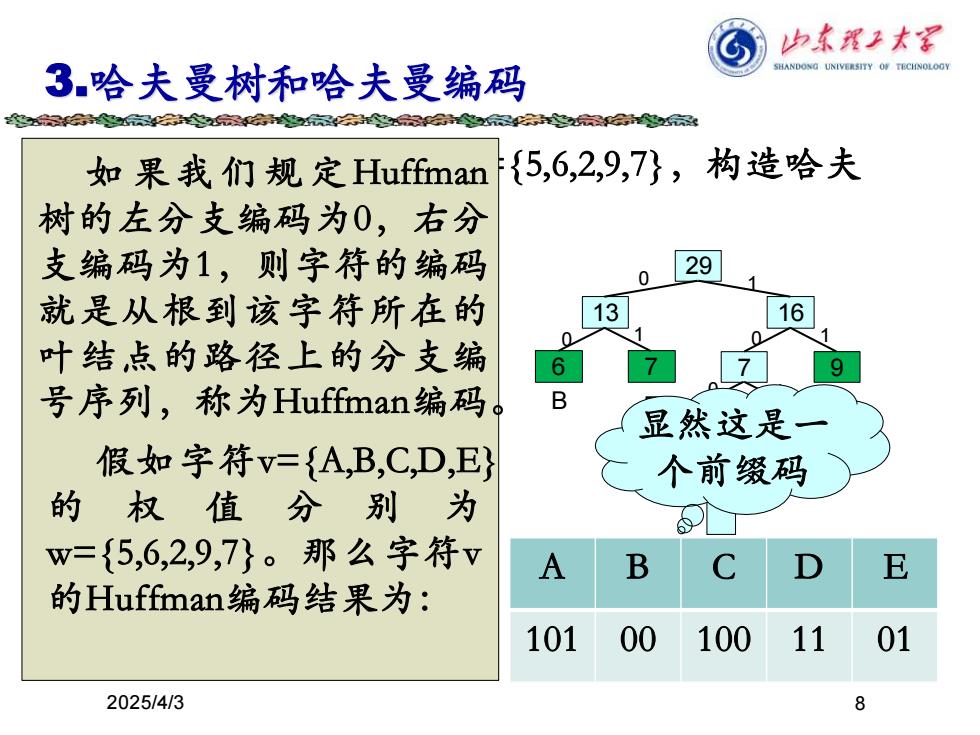
8 3.哈夫曼树和哈夫曼编码 例:已知权值的集合W={5,6,2,9,7},构造哈夫 曼树。 2025/4/3 5 6 2 9 7 6 9 7 7 2 5 9 13 7 6 7 2 5 7 9 13 7 2 5 6 16 7 9 13 7 2 5 6 16 29 0 0 0 0 1 1 1 1 如 果我 们规定 Huffman 树的左分支编码为0,右分 支编码为1,则字符的编码 就是从根到该字符所在的 叶结点的路径上的分支编 号序列,称为Huffman编码。 假如字符v={A,B,C,D,E} 的 权 值 分 别 为 w={5,6,2,9,7}。那么字符v 的Huffman编码结果为: A B C D E 101 00 100 11 01 E D C B A 显然这是一 个前缀码