
第4卷第4期 智能系统学报 Vol.4 No.4 2009年8月 CAAI Transactions on Intelligent Systems Ag.2009 doi:10.3969/j.issn.16734785.2009.04.010 一种新型自适应RBF神经网络滑模制导律 章钱,李士勇 (哈尔滨工业大学航天学院,黑龙江哈尔滨150001) 摘要:针对导弹拦截问题,提出一种自适应RBF神经网络滑模制导律.首先根据准平行接近原理和变结构控制理 论设计滑模面,然后将滑模面作为RBF神经网络的输入变量,输出量即为导弹的加速度.为了使得导弹系统能够到 达滑模面,采用自适应算法实时在线调整RBF神经网络的连接权值.该导引律将目标机动视为干扰量,在拦截过程 中不需要测量目标加速度,因此该导引律对目标机动具有较强的鲁棒性.在执行上,只用到了视线角速率,因而实现 简单.仿真结果表明,所提出的导引律和比例导引相比在脱靶量、拦截时间等方面有了很大的提高. 关键词:自适应控制;RBF神经网络;导弹拦截;滑模控制:比例导引律 中图分类号:T叮765.3文献标识码:A文章编号:16734785(2009)04033906 A new adaptive RBFNN sliding mode guidance law for intercepting maneuvering targets ZHANG Qian,LI Shi-yong (School of Astronautics,Harbin Institute of Technology,Harbin 150001,China) Abstract:A new adaptive radial basis function neural network (RBFNN)sliding mode guidance law was proposed for intercepting maneuvering targets.First of all,we designed a sliding-surface using a quasi-parallel approach principle and variable structure control theory.We then used the sliding surface to input variables to the RBF neu- ral network.In this case,the output was missile acceleration.In order to place the missile system on the sliding surface,we employed an adaptive algorithm that adjusts in real-time the connection weights of the RBF neural net- work.The missile acceleration in a given direction was determined by considering the targets acceleration as a dis- turbance,and thus it was not necessary to measure the targets acceleration directly.Therefore,this guidance law has strong robustness to target maneuvering.The new guidance law,which utilizes line-of-sight (LOS)measure- ment only,is simple to implement.Numerical simulations showed that the proposed guidance law yields better per- formance than proportional navigation. Keywords:adaptive control;RBFNN;missile intercept;sliding model control;proportional navigation 自从20世纪50年代提出比例导引律后,由于较复杂,不利于工程实现. 其实现简单,能有效对付低速小机动目标,因而获得 变结构控制(sliding model control)理论对外部 了较快的发展,先后出现了纯比例导引(PPN)、真比 干扰和参数摄动具有较强的鲁棒性,因此采用滑模 例导引(TPN)以及扩展比例导引(APN)等.但到了 变结构控制是解决导弹制导问题较好的途径.近几 20世纪80年代,高速、大机动目标的出现使得传统 年在该方面的研究较多,设计出了很多制导律.针对 的比例导引律不能达到满意的拦截效果。 线性时变系统的滑动模态运动对于扰动和参数摄动 自适应控制对参数不确定或未知的系统具有较 具有鲁棒性的特点,D.Zou等提出了一种自适应滑 好的控制效果.近年来,基于自适应控制的制导 模制导律ASMG4;文献[5]在非线性系统的基础 律131得到较快发展,它们在对付高速大机动目标 上,应用变结构控制,推导出一种非线性变结构制导 时的拦截精度优于传统制导律.但它们的形式都比 律.虽然上述文献中的变结构制导律在制导过程中 无需测量目标机动的精确值,但无一例外,都需要知 收稿日期:200904-15, 基金项目:国家自然科学基金资助项目(60773065). 道目标机动的上限值.而在实际导弹拦截系统中,目 通信作者:章钱.E-mai:qz50306@163.com. 标机动的上界值一般很难预先测量,且由于存在抖

·340 智能系统学报 第4卷 振6,因此限制了其应用 sin g(t)=ja(t)/R(t). (1) RBF神经网络(RBFNN)由于具有良好的逼近 式中:R(t)为导弹与目标之间的相对距离;少3(t)为 非线性光滑函数以及快速运算的能力而被广泛应用 △t时间内y3方向上的相对位移.若△t足够小,则 到控制系统设计中?1.Abedi等人8]考虑了目标机 ()为小量,故可近似为 动和导弹动态不确定性,使用RBF神经网络来自适 g(t)=y3(t)/R(t): (2) 应地补偿模型的非线性.RBF网络的权值采用Lya- 将式(2)对时间3次微分,得到 punov理论来设计,另外还采用了自适应补偿器来 9=-2(t)-(k1+石2))(t)-系9+ 测量误差和外界干扰.胡云安等1o]使用RBF神经 3(t)+353(t). (3) 网络在线辨识和补偿系统中存在的不确定性,并采 式中: 用自适应律来调节RBF网络的权重.Gu等人)提 R(t) 出了基于RBF神经网络的三维纯比例制导律 h=R(t)' (PNGLRBF),由于传统的比例导引律的导航比系数 固定,因此会造成较大脱靶量,针对这个问题,文中 6智, 提出利用RBF神经网络在线实时调整导航比系数, 1 产生最优的加速度指令.仿真结果表明作者提出的 店=R(G)' 制导律能够显著地减小脱靶量. 3(t)=-aa(t)+a3(t). (4) 本文设计了一种新的自适应RBF滑模控制器 式中:am3(t)与a3(t)分别为导弹和目标机动加速 adaptive RBFNN sliding model controller,ARBF- 度在y3方向上的分量.将式(4)代入式(3)可得: SM),综合了变结构控制、自适应算法以及RBFNN (t)=a19(t)+a2(t)+ 的优点,并将其应用于导弹制导中.控制策略是设计 a3q as +u(t)ua(t). (5) 特定的滑模面,然后将滑模面作为RBFNN的输入 式中: 变量,输出量即为导弹控制量加速度.自适应算法根 a1=-k2,a2=-(k1+2), 据可达条件实时在线调整RBF神经网络的连接权 a3=-无1,a4=-k3dm3(t), 值,从而使得系统最终到达滑模面,完成制导.仿真 ua(t)=ka(aca(t)+aga(t)), 结果表明了该制导律的有效性, u(t)=3am3(t). 1导弹一目标运动方程 选取状态变量x1=9,x2=9,则式(5)可表示为 「1=2, 为了研究导引规律,选取某一时间区间△:起始 (6) =f(t)-u(t)+u(t) 时刻的视线坐标系(x3y)作为末制导过程中目 标一导弹相对运动的参考坐标系),如图1所示. 式中:f()=a1(t)+a2(t)+a39+a4,是知时变函 原点o取为导弹当前时刻的质心,x3轴取为导弹初 数;u(t)为控制量,uu(t)视为外界干扰. 始视线角方向,y3轴与3轴垂直且指向上为正,3 2 制导律设计 轴由右手定则确定.在△内,此参考系仅随导弹平 动,这样末制导过程中的相对运动可以解耦成纵向 根据准平行接近原理希望(t)在制导过程中 平面0xy3内的运动和侧向平面x3内的运动. 趋于零,因此可选取滑模面415] s(t)=g(t)+入9(t). (7) 式中:A=const>O,ARBFSM的原理是将滑模面s作 为RBFNN的输入量,RBFNN的输出为控制量u(t). 在制导过程中,通过自适应算法不断调整RBFNN o(M 隐含层神经元与输出层神经元之间的连接权重,产 生的控制量使得系统逐渐趋向滑模面并最终停留在 滑模面上,最终完成拦截任务。 图1视线坐标系 设RBF网络的径向基向量h=[h,h2…hm]T, Fig.1 The LOS coordinate system 其中为高斯基函数16] 以纵向平面内的运动为例,设在△:内,视线倾 6=c(-1X-)=ep(-1-5), 角的增量为(t)(为简化,用(t)表示g,(t),则

第4期 章钱,等:一种新型自适应RBF神经网络滑模制导律 ·341· j=1,2,…,m (8) 上述分析,可得出ARBFSM制导律的系统方框图如 式中:m为隐含层神经元个数,c;=[ccn 图2所示.另外,一般应用中,高斯函数中的参数σ c]T为RBFNN的第j个隐含层单元的中心向量; 和c,可以固定为常数, 0=[σ102…0m],0为第j个隐含层单元的 3稳定性分析 基宽参数,且大于零,即为高斯型函数的基宽 设RBFNN的权向量为 Lyapunov稳定性分析方法较广泛地应用于证 w=[0102 …0n] (9) 明非线性系统的收敛中,下面利用Lyapunov法来检 故RBF网络的输出为 验提出的ARBFSM控制器的稳定性, 4=w,ep(--9). 若式(6)中时变函数f(t)精确已知,则理想的 (10) 控制律可以写为 由Lyapunov理论可知,滑模面可达的条件是ss<O. uag =f(t)+ua(t)-2(t)+s(t)+As(t). 如果能够选择适当的控制量u(t),使可达条件成 (16) 立,那么控制系统将会收敛于设计的滑模面上.由于 将式(16)代入式(6),可得 RBFNN用来近似滑模面与输出控制量之间的非线 s(t)+As(t)=0. (17) 性映射,因此RBFNN的连接权值应该根据可达条 由于入>0,故必有s(t)s(t)<0,因此滑模面s 件s“<0来不断地调整.故采用自适应算法来寻找 将收敛于0.由方程(7)定义的滑模面可知,系统输 最优权值,从而最小化$的值,使其不断趋向于零. 出(t)也会收敛于0,进而最终完成拦截要求.在分 由上述分析可知,RBFNN的权值调整指标可写为 析中,RBFNN用来近似滑模面s与输出控制量u(t) E=s(t)s(t). (11) 的非线性映射,而取代了传统的基于精确模型的计 则根据梯度下降法有 算,因此输出控制量u(t)与理想控制量“之间可能 4=-yas9=-yas909 会存在误差.由式(6)与式(16)可得 0o,(t) au(t)o;(t) s(t)=-As(t)+(uo -u(t)). (18) (12) 理论上,RBFNN能够以任何精度逼近任何非线 式中:y为自适应律参数.由于 性函数,因此可以做出如下假设: as()()=()( =-s(t), (13) 假设存在最优权值向量W,使得RBNN输出 0u(t) au(t) 控制量u(t)与理想控制量uw之间的最大误差为 au(t) aw;(t) =exp(-s=9. (14) 也即 max|u(x,W)-ug|≤5 (19) 故式(12)可写为 号=50ep(-s-5)=04. 式中:u(x,W)=∑-1whk=Wh,ug=Wh+专,专 (15) 为一小正数 设W=W-巾为最优权向量与当前估计权向 量之间的误差,则式(18)可改写为 攻角c s(t)=-As(t)+(h+专). (20) ()=AG()+(t) 俯仰通道 选择Lyapunov函数为 v-2+ (21) 自适应律 w=ys(t)hAs} 将式(21)对时间进行微分得 )导弹-日标 导弹力学系统 p=s对+1mm. (22) 相对运动 目标运动 将方程(15)、(20)代人(22),可得 图2 ARBFSM制导系统方框图 V=s[-As(t)+(rh+)]-s= Fig.2 The block diagram of ARBFSM guidance system -As2+s装≤1s1(-A1s1+).(23) 如果选择|s|>/入,则V<0.这意味着Lya 通过式(15)可以使得隐含层神经元与输出层 punov函数将逐渐减小,滑模面s将会收敛于s=O 神经元之间的连接权值w实时调整,以实现 的界限层/入内.从上述分析可知,提出的ARBFSM RBFNN的在线学习,因此,的初始值可以为O.由 控制器是稳定的,由滑模面的定义可知,I(t)I会
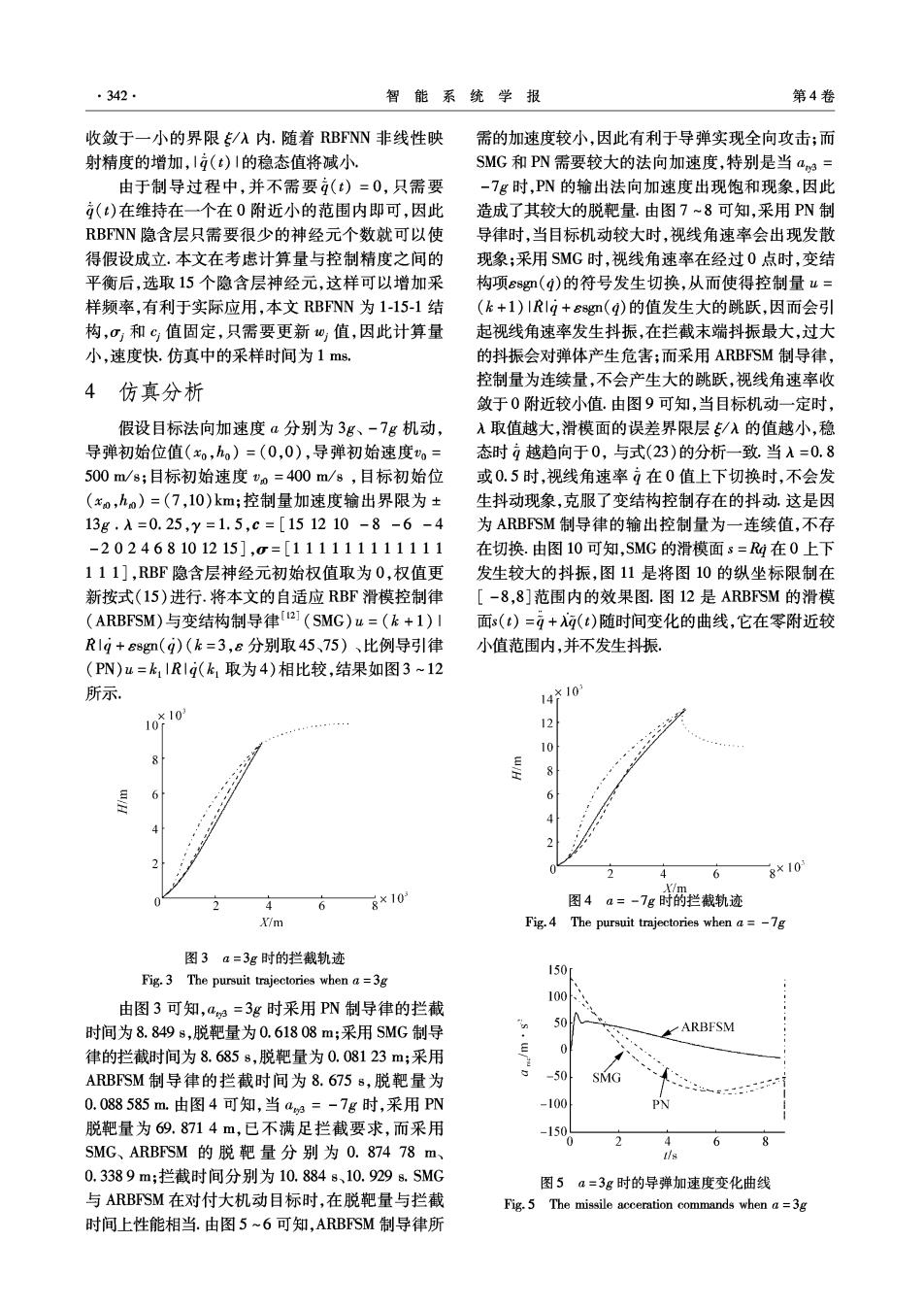
342. 智能系统学报 第4卷 收敛于一小的界限/入内.随着RBFNN非线性映 需的加速度较小,因此有利于导弹实现全向攻击;而 射精度的增加,I(t)1的稳态值将减小 SMG和PN需要较大的法向加速度,特别是当a3= 由于制导过程中,并不需要(t)=0,只需要 -7g时,PN的输出法向加速度出现饱和现象,因此 ()在维持在一个在0附近小的范围内即可,因此 造成了其较大的脱靶量.由图7~8可知,采用PN制 RBFNN隐含层只需要很少的神经元个数就可以使 导律时,当目标机动较大时,视线角速率会出现发散 得假设成立.本文在考虑计算量与控制精度之间的 现象;采用SMG时,视线角速率在经过0点时,变结 平衡后,选取15个隐含层神经元,这样可以增加采 构项εsg(q)的符号发生切换,从而使得控制量w= 样频率,有利于实际应用,本文RBFNN为1-15-1结 (k+1)川R19+6g(q)的值发生大的跳跃,因而会引 构,σ和℃值固定,只需要更新0值,因此计算量 起视线角速率发生抖振,在拦截末端抖振最大,过大 小,速度快.仿真中的采样时间为1ms. 的抖振会对弹体产生危害;而采用ARBFSM制导律, 4 仿真分析 控制量为连续量,不会产生大的跳跃,视线角速率收 敛于0附近较小值.由图9可知,当目标机动一定时, 假设目标法向加速度a分别为3g、-7g机动, 入取值越大,滑模面的误差界限层/入的值越小,稳 导弹初始位值(o,h)=(0,0),导弹初始速度o= 态时越趋向于0,与式(23)的分析一致.当入=0.8 500m/s;目标初始速度vo=400m/s,目标初始位 或0.5时,视线角速率在0值上下切换时,不会发 (xo,ho)=(7,l0)km;控制量加速度输出界限为± 生抖动现象,克服了变结构控制存在的抖动.这是因 13g.入=0.25,y=1.5,c=[151210-8-6-4 为ARBFSM制导律的输出控制量为一连续值,不存 -202468101215],0=[111111111111 在切换.由图10可知,SMG的滑模面s=R4在0上下 111],RBF隐含层神经元初始权值取为0,权值更 发生较大的抖振,图11是将图10的纵坐标限制在 新按式(15)进行.将本文的自适应RBF滑模控制律 [-8,8]范围内的效果图.图12是ARBFSM的滑模 (ARBFSM)与变结构制导律2I(SMG)u=(k+1)I 面s(t)=g+()随时间变化的曲线,它在零附近较 R1g+88g(9)(k=3,8分别取45、75)、比例导引律 小值范围内,并不发生抖振 (PN)u=kIR1g(k1取为4)相比较,结果如图3~12 所示 14*10 ×10 10 12 10 8 6 2 4 6 8×10 X/m 4 8×10 图4a=-7g时的拦截轨迹 X/m Fig.4 The pursuit trajectories when a=-7g 图3a=3g时的拦截轨迹 150r Fig.3 The pursuit trajectories when a=3g 100 由图3可知,ag=3g时采用PN制导律的拦截 时间为8.849s,脱靶量为0.61808m;采用SMG制导 50八 ARBFSM 律的拦截时间为8.685s,脱靶量为0.08123m;采用 0 ARBFSM制导律的拦截时间为8.675s,脱靶量为 -50 SMG 0.088585m.由图4可知,当aa=-7g时,采用PN -100 PN 脱靶量为69.8714m,已不满足拦截要求,而采用 -150 6 R SMG、ARBFSM的脱靶量分别为0.87478m、 t/s 0.3389m;拦截时间分别为10.884s、10.9298.SMG 图5a=3g时的导弹加速度变化曲线 与ARBFSM在对付大机动目标时,在脱靶量与拦截 Fig.5 The missile acceration commands when a=3g 时间上性能相当.由图5~6可知,ARBFSM制导律所
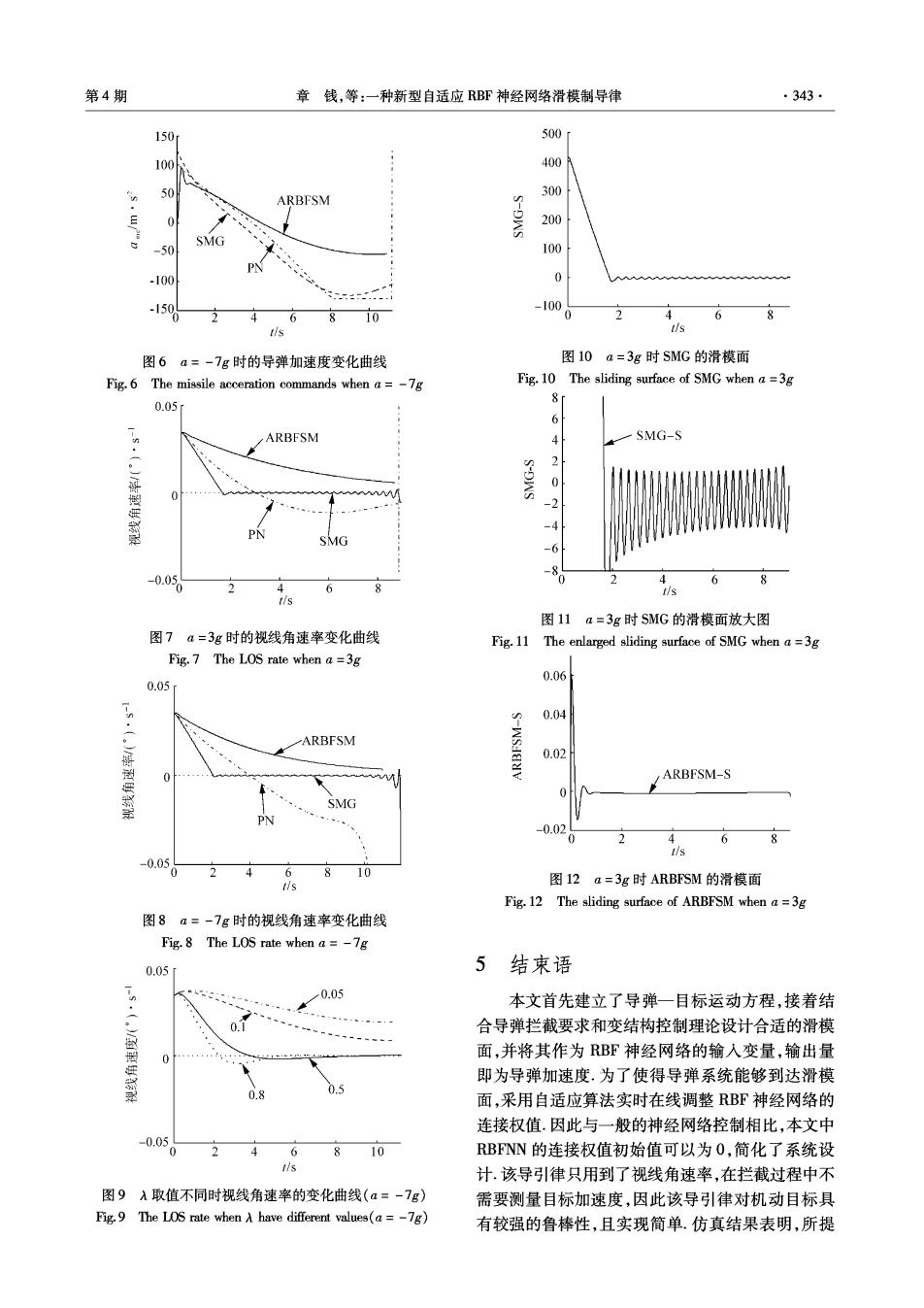
第4期 章钱,等:一种新型自适应RBF神经网络滑模制导律 343. 150 500 100 400 50 300 ARBFSM 0 200 SMG -50 100 PN -100 -100 6 810 4 6 8 tis t/s 图6 a=-7g时的导弹加速度变化曲线 图10a=3g时SMG的滑模面 Fig.6 The missile acceration commands when a =-7g Fig.10 The sliding surface of SMG when a=3g 0.05 f 6 ARBFSM SMG-S 2 0 0 S-DWS -2 PN -4 SMG -6 0.056 -8 0 6 4 tis t/s 图11a=3g时SMG的滑模面放大图 图7a=3g时的视线角速率变化曲线 Fig.11 The enlarged sliding surface of SMG when a=3g Fig.7 The LOS rate when a=3g 0.06 0.05 0.04 ARBFSM 0.02 0 ARBFSM-S SMG PN -0.02 68 ts -0.0 0 2 4 6 810 图12a=3g时ARBFSM的滑模面 Fig.12 The sliding surface of ARBFSM when a=3g 图8α=-7g时的视线角速率变化曲线 Fig.8 The LOS rate when a=-7g 0.05 5结束语 0.05 本文首先建立了导弹一目标运动方程,接着结 合导弹拦截要求和变结构控制理论设计合适的滑模 - 面,并将其作为RBF神经网络的输入变量,输出量 即为导弹加速度.为了使得导弹系统能够到达滑模 0.8 0.5 面,采用自适应算法实时在线调整RBF神经网络的 连接权值.因此与一般的神经网络控制相比,本文中 -0.05 0 4 6 RBFNN的连接权值初始值可以为O,简化了系统设 dis 计.该导引律只用到了视线角速率,在拦截过程中不 图9入取值不同时视线角速率的变化曲线(a=-7g) 需要测量目标加速度,因此该导引律对机动目标具 Fig.9 The LOS rate when A have different values(a =-7g) 有较强的鲁棒性,且实现简单.仿真结果表明,所提