
China-pub.com 下载 第1章1 MATLAB是什么 没有MATLAB就没有乐趣。 Nachtigal,M.N.,Reddy,S.C.,Trefethen,L.N.(1990). 不对称矩阵迭代有多快? 关于迭代方法的Copper Mountain会议论文集, Copper Mountain C0,1-5,1990年4月。 1.1 MATLAB能做什么 MATLAB是一个可视化的计算程序,被广泛地使用于从个人计算机到超级计算机范围内 的各种计算机上。 MATLAB包括命令控制、可编程,有上百个预先定义好的命令和函数。这些函数能通过 用户自定义函数进一步扩展。 MATLAB有许多强有力的命令。例如,MATLAB能够用一个单一的命令求解线性系统, 能完成大量的高级矩阵处理。 MATLAB有强有力的二维、三维图形工具。 MATLAB能与其他程序一起使用。例如,MATLAB的图形功能,可以在一个FORTRAN 程序中完成可视化计算。 25个不同的MATLAB工具箱可应用于特殊的应用领域。 MATLAB在以下的领域里解决各种问题是一个十分有效的工具: ·工业研究与开发。 ·数学教学,特别是线性代数。所有基本概念都能涉及。 ·在数值分析和科学计算方面的教学与研究。能够详细地研究和比较各种算法。 ·在诸如电子学、控制理论和物理学等工程和科学学科方面的教学与研究。 ·在诸如经济学、化学和生物学等有计算问题的所有其他领域中的教学与研究。 ·在MATLAB中创建的组是矩阵,MATLAB的名字取自矩阵实验室(MATrix LABoratory)。 1.2 MATLAB实例 本节中的实例恰当而简洁地展示了MATLAB能做什么。在一些实例中给出了完整的 MATLAB命令:而在另一些实例中,为简化仅给出部分命令。 在本书中出现的MATLAB代码用的是一种特殊的字体以区别于书中别的文字。 MATLAB的输出是斜体字,即:我们输给MATLAB的命令是正体:MATLAB给出的输出答 案是斜体。 百分符号%在MATLAB中用做注释符号,在本书中全部都是这样使用。采用的其他表示 方法是:数量和预定义函数用斜体字,矩阵、向量和用户自定义函数用黑体字。矩阵用大写
下载 第1章 M AT L A B是什么 没有M AT L A B就没有乐趣。 Nachtigal, M. N., Reddy, S. C., Trefethen, L.N.(1990)。 不对称矩阵迭代有多快? 关于迭代方法的Copper Mountain会议论文集, Copper Mountain CO, 1-5,1990年4月。 1.1 MAT L A B能做什么 M AT L A B是一个可视化的计算程序,被广泛地使用于从个人计算机到超级计算机范围内 的各种计算机上。 M AT L A B包括命令控制、可编程,有上百个预先定义好的命令和函数。这些函数能通过 用户自定义函数进一步扩展。 M AT L A B有许多强有力的命令。例如, M AT L A B能够用一个单一的命令求解线性系统, 能完成大量的高级矩阵处理。 M AT L A B有强有力的二维、三维图形工具。 M AT L A B能与其他程序一起使用。例如, M AT L A B的图形功能,可以在一个 F O RT R A N 程序中完成可视化计算。 2 5个不同的M AT L A B工具箱可应用于特殊的应用领域。 M AT L A B在以下的领域里解决各种问题是一个十分有效的工具: • 工业研究与开发。 • 数学教学,特别是线性代数。所有基本概念都能涉及。 • 在数值分析和科学计算方面的教学与研究。能够详细地研究和比较各种算法。 • 在诸如电子学、控制理论和物理学等工程和科学学科方面的教学与研究。 • 在诸如经济学、化学和生物学等有计算问题的所有其他领域中的教学与研究。 • 在M AT L A B中创建的组是矩阵,M AT L A B的名字取自矩阵实验室( M ATrix LABoratory)。 1.2 MAT L A B实例 本节中的实例恰当而简洁地展示了 M AT L A B能做什么。在一些实例中给出了完整的 M AT L A B命令;而在另一些实例中,为简化仅给出部分命令。 在本书中出现的 M AT L A B 代码用的是一种特殊的字体以区别于书中别的文字。 M AT L A B的输出是斜体字,即:我们输给 M AT L A B的命令是正体; M AT L A B给出的输出答 案是斜体。 百分符号%在M AT L A B中用做注释符号,在本书中全部都是这样使用。采用的其他表示 方法是:数量和预定义函数用斜体字,矩阵、向量和用户自定义函数用黑体字。矩阵用大写

China-pub.com MATLAB5手册 下载 字母开头命名,而向量以小写字母开头。细胞矩阵是如同矩阵或向量的概念,也采用黑体字, 其结构和对象也是如此。在命令表中,用斜体字表示那些可选的函数参数。例如, command(parl,par2),参数parl总是需要的,而par2是可选的。 ■例1.1二维和三维函数 MATLAB能用于计算,并以二维和三维图形显示各种函数。在MATLAB函数中包括了所 有主要的数学函数和大量的高级函数。 (a)用简短的MATLAB命令计算并绘制在0≤x≤6范围内的sin(2x)、sinr和sinx。 x=linspace(0,6);号创建一个向量x y1=sin(2*x);告向量y1等于x坐标上某一x的sin(2x)值。 y2=sin(x.^2); 号向量y2等于sin(x.^2),同上。 y3=(sin(x).2;号向量y3等于(sin(x).^2,同上。 命令p1ot(x,y1)绘制向量y1,y1作为向量x的一个函数,p1ot命令的定义可参见第13 章。由此能够很容易地在一个图上绘制sin(2x)、sin(x2)和sinx的曲线并正确地标记它们(图1-1)。 02 : 20 图11同一图上的三条曲线 (b)两个变量的函数需要用三维来恰当地图示,MATLAB能够给出很好的三维图。在图-2中,用 四个不同的方法展示了函数x,)=cosx)·sin)的图形:左上图用urf命令和heding interp:右 上图用mesh:左下图用waterfall以及右下图用contour。关于图像命令的详细信息可参见第3章。 用surf和shading interp绘图 用mesh绘图 00 用mesh和隐藏线绘图 用contour绘图 30 图1-2四种方法绘制双变量的一个函数的图形
字母开头命名,而向量以小写字母开头。细胞矩阵是如同矩阵或向量的概念,也采用黑体字, 其结构和对象也是如此。在命令表中,用斜体字表示那些可选的函数参数。例如, c o m m a n d (parl, p a r2),参数p a r 1总是需要的,而p a r2是可选的。 ■ 例1.1 二维和三维函数 M AT L A B能用于计算,并以二维和三维图形显示各种函数。在 M AT L A B函数中包括了所 有主要的数学函数和大量的高级函数。 (a) 用简短的M AT L A B命令计算并绘制在0≤x≤6范围内的s i n ( 2x)、s i nx 2和s i n2x。 x = l i n s p a c e ( 0 , 6 ) ; % 创建一个向量x。 y 1 = s i n ( 2*x ) ; % 向量y 1等于x坐标上某一x的s i n ( 2 x )值。 y 2 = s i n ( x . ^ 2 ) ; % 向量y 2等于s i n ( x . ^ 2 ),同上。 y 3 = ( s i n ( x ) ) . ^ 2 ; % 向量y 3等于( s i n ( x ) ) . ^ 2,同上。 命令p l o t ( x , y 1 )绘制向量y 1,y 1作为向量x的一个函数,p l o t命令的定义可参见第 1 3 章。由此能够很容易地在一个图上绘制 s i n ( 2x)、s i n (x 2 )和s i n2x的曲线并正确地标记它们(图1 - 1 )。 图1-1 同一图上的三条曲线 (b) 两个变量的函数需要用三维来恰当地图示,M AT L A B能够给出很好的三维图。在图1 - 2中,用 四个不同的方法展示了函数f(x, y) = cos (x)·sin (y)的图形:左上图用s u r f命令和shading interp ;右 上图用m e s h;左下图用w a t e r f a l l以及右下图用c o n t o u r。关于图像命令的详细信息可参见第1 3章。 图1-2 四种方法绘制双变量的一个函数的图形 2 M ATLAB 5 手册 下载 用surf和shading interp绘图 用mesh绘图 用mesh和隐藏线绘图 用contour绘图
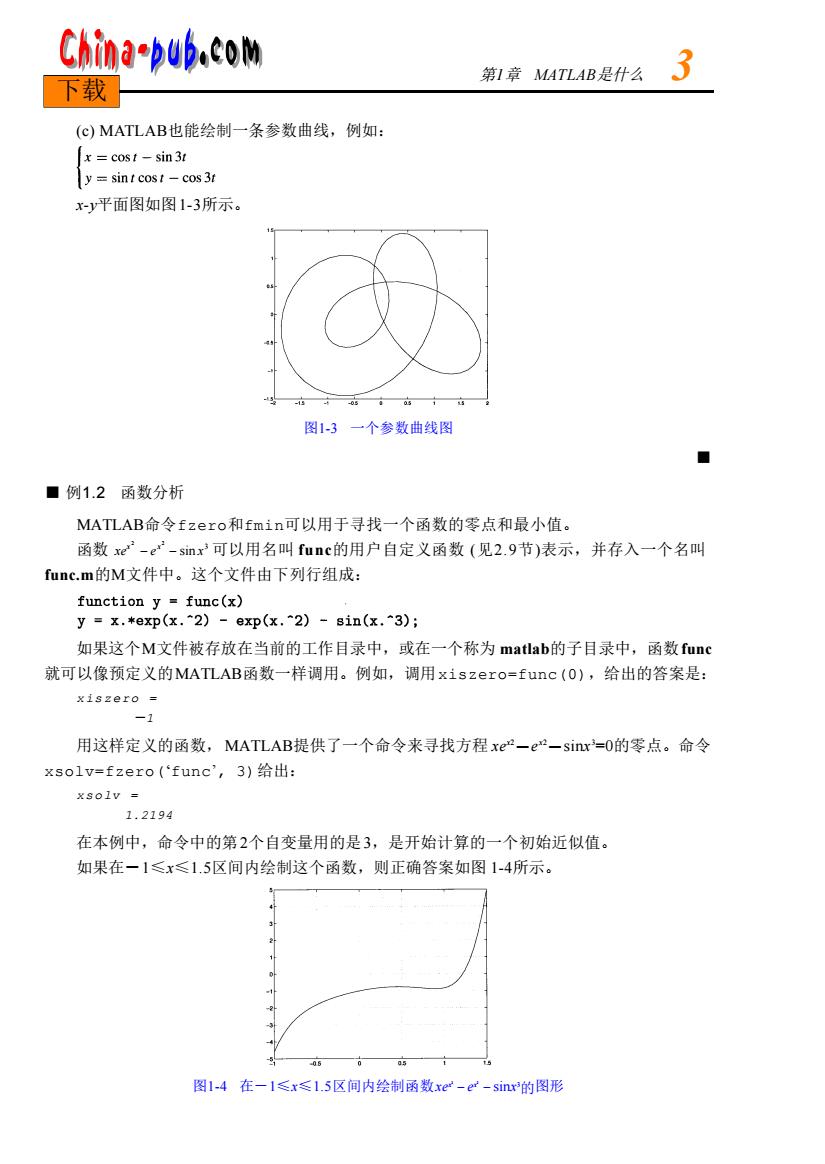
China-pub.com 第I章ATLAB是什么 下载 (c)MATLAB也能绘制一条参数曲线,例如: x cost-sin 3t y sint cost -cos 3t x-y平面图如图1-3所示。 -05 图1-3一个参数曲线图 ■ ■例1.2函数分析 MATLAB命令fzero和fmin可以用于寻找一个函数的零点和最小值。 函数xe-e-smr可以用名叫func的用户自定义函数(见2.9节)表示,并存入一个名叫 func.m的M文件中。这个文件由下列行组成: function y=func(x) y=x.*exp(x.2)-exp(x.2)-8in(x.^3); 如果这个M文件被存放在当前的工作目录中,或在一个称为matlab的子目录中,函数func 就可以像预定义的MATLAB函数一样调用。例如,调用xiszero=func(O),给出的答案是: xiszero -1 用这样定义的函数,MATLAB提供了一个命令来寻找方程xe2一e2一sinx=0的零点。命令 xsolv=fzero(‘func',3)给出: xsolv 1.2194 在本例中,命令中的第2个自变量用的是3,是开始计算的一个初始近似值。 如果在一1≤x≤1.5区间内绘制这个函数,则正确答案如图1-4所示。 0 05 图1-4在-1≤x≤1.5区间内绘制函数xe-e-sinr的图形
(c) MAT L A B也能绘制一条参数曲线,例如: x-y平面图如图1 - 3所示。 图1-3 一个参数曲线图 ■ 例1.2 函数分析 M AT L A B命令f z e r o和f m i n可以用于寻找一个函数的零点和最小值。 函数 可以用名叫 f u n c的用户自定义函数 (见2 . 9节)表示,并存入一个名叫 f u n c . m的M文件中。这个文件由下列行组成: 如果这个M文件被存放在当前的工作目录中,或在一个称为 m a t l a b的子目录中,函数f u n c 就可以像预定义的M AT L A B函数一样调用。例如,调用x i s z e r o = f u n c ( 0 ),给出的答案是: xiszero = -1 用这样定义的函数,M AT L A B提供了一个命令来寻找方程 x ex2-e x2-s i nx 3= 0的零点。命令 x s o l v = f z e r o (‘f u n c’, 3)给出: xsolv = 1 . 2 1 9 4 在本例中,命令中的第2个自变量用的是3,是开始计算的一个初始近似值。 如果在-1≤x≤1 . 5区间内绘制这个函数,则正确答案如图 1 - 4所示。 图1-4 在-1≤x≤1 . 5区间内绘制函数xex 2-e x 2-sinx 3的图形 xe x 2 - e x 2 - sin x 3 第1章 M AT L A B是什么 3 下载 ■

China-pub.com MATLAB5手册 下载 当x在0.5和1之间时,这个函数看起来有一个极小值,为正确找出这个极小值,用命令 mpoint=fmin(‘func',0.5,1)其结果为: mpoint 0.8954 用于检查MATLAB中用户自定义函数的命令可参见第10章和第11章。 ■ ■例1.3线性系统与特征值 ()MATLAB可以用一个简单的命令行求解线性系统,系数矩阵A和右侧b定义如下: -(-(韵 6 .1 这对应于线性系统Ax=b,如下所示: 3x1+x2-x3=3.6 x1+2x2+4x3=2.1 -x1+4x2+5x3=-1.4 这可由如下命令求解: x=A\b 其结果为: X 1.4818 -0.4606 0.3848 (b)还有许多矩阵控制命令。例如,例()中矩阵A的特征值很容易地可以由下列命令得到: [EigenVectors,EigenValues]eig(A) 其给出: EigenVectors -0.9482 -0.3129 -0.0553 -0.2887 0.7756 0.5613 0.1328 -0.5482 0.8258 EigenValues 3.4445 0 0 0 -1.2305 0 0 0 7.7860 矩阵Eigen Vectors的列是A的特征向量,Eigen Values中对角线元素是特征值。由于矩阵A 是对称的,因此,所有的特征值都是实数,三个特征向量是相互正交的。 ■ MATLAB中的基本概念是矩阵。基本的矩阵命令在第3章描述,更多的命令将在第4、7、 8、9章中描述。 ■例1.4曲线拟合与插值 ()如果有两个向量x和y表示的x-y平面上的一组点,那么,可以对它们进行插值点或者拟 合一条曲线。令 x=(11.534566.578)
当x在0 . 5和1之间时,这个函数看起来有一个极小值,为正确找出这个极小值,用命令 m p o i n t = f m i n (‘f u n c’, 0.5, 1),其结果为: mpoint = 0 . 8 9 5 4 用于检查M AT L A B中用户自定义函数的命令可参见第 1 0章和第11章。 ■ 例1.3 线性系统与特征值 (a) MAT L A B可以用一个简单的命令行求解线性系统,系数矩阵 A和右侧b定义如下: 这对应于线性系统A x = b,如下所示: 这可由如下命令求解: x = A \ b 其结果为: (b) 还有许多矩阵控制命令。例如,例 ( a )中矩阵A的特征值很容易地可以由下列命令得到: 其给出: 矩阵E i g e n Ve c t o r s的列是A的特征向量,E i g e n Va l u e s中对角线元素是特征值。由于矩阵 A 是对称的,因此,所有的特征值都是实数,三个特征向量是相互正交的。 M AT L A B中的基本概念是矩阵。基本的矩阵命令在第 3章描述,更多的命令将在第 4、7、 8、9章中描述。 ■ 例1.4 曲线拟合与插值 (a) 如果有两个向量x和y表示的x-y平面上的一组点,那么,可以对它们进行插值点或者拟 合一条曲线。令 4 M ATLAB 5 手册 下载 ■ ■
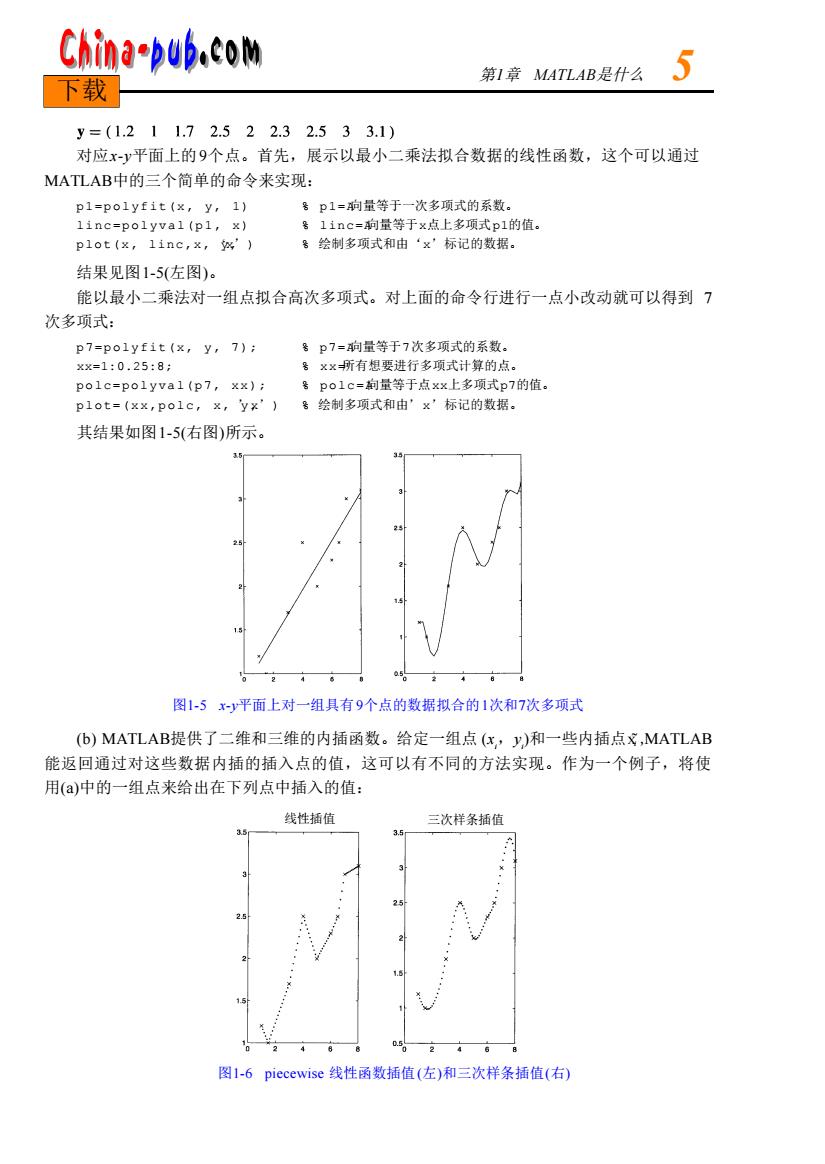
China-pub.com 第I章ATLAB是什么 下载 y=(1.211.72.522.32.533.1) 对应x-y平面上的9个点。首先,展示以最小二乘法拟合数据的线性函数,这个可以通过 MATLAB中的三个简单的命令来实现: pl=polyfit(x,y,1) 号P1=向量等于一次多项式的系数。 linc=polyval(pl,x) 号1inc=向量等于x点上多项式p1的值。 plot(x,linc,x,) 告绘制多项式和由‘x'标记的数据。 结果见图1-5(左图)。 能以最小二乘法对一组点拟合高次多项式。对上面的命令行进行一点小改动就可以得到7 次多项式: p7=polyfit(x,y,7); 号p7=向量等于7次多项式的系数。 xx=1:0.25:8: 号xx所有想要进行多项式计算的点。 po1c=po1yva1(p7,x);号po1c=甸量等于点xx上多项式p7的值。 P1ot=(xx,Po1c,,y×”)号绘制多项式和由'x'标记的数据。 其结果如图1-5(右图)所示。 图1-5xy平面上对一组具有9个点的数据拟合的1次和7次多项式 (b)MATLAB提供了二维和三维的内插函数。给定一组点(x,y)和一些内插点X,MATLAB 能返回通过对这些数据内插的插入点的值,这可以有不同的方法实现。作为一个例子,将使 用(a)中的一组点来给出在下列点中插入的值: 线性插值 三次样条插值 0.5 图1-6.piecewise线性函数插值(左)和三次样条插值(右)
对应x-y平面上的9个点。首先,展示以最小二乘法拟合数据的线性函数,这个可以通过 M AT L A B中的三个简单的命令来实现: p1=polyfit(x, y, 1) % p1=A向量等于一次多项式的系数。 linc=polyval(p1, x) % linc=A向量等于x点上多项式p 1的值。 plot(x, linc,x, y,‘x’) % 绘制多项式和由‘x’标记的数据。 结果见图1 - 5 (左图)。 能以最小二乘法对一组点拟合高次多项式。对上面的命令行进行一点小改动就可以得到 7 次多项式: p7=polyfit(x, y, 7); % p7=A向量等于7次多项式的系数。 x x = 1 : 0 . 2 5 : 8 ; % xx=所有想要进行多项式计算的点。 polc=polyval(p7, xx); % polc=A向量等于点x x上多项式p 7的值。 plot=(xx,polc, x, y, ’x’) % 绘制多项式和由’x’标记的数据。 其结果如图1 - 5 (右图)所示。 图1-5 x-y平面上对一组具有9个点的数据拟合的1次和7次多项式 (b) MAT L A B提供了二维和三维的内插函数。给定一组点 (x i,y i )和一些内插点x˜i ,M AT L A B 能返回通过对这些数据内插的插入点的值,这可以有不同的方法实现。作为一个例子,将使 用( a )中的一组点来给出在下列点中插入的值: 图1-6 piecewise 线性函数插值(左)和三次样条插值(右) 第1章 M AT L A B是什么 5 下载 线性插值 三次样条插值