
归本程上太军 SHANDONG UNIVERSITY OF TECHNOLOGY 建立递归关系 可以递归地定义m[i,j]为: 0 i=i mli,j]= min {mli,k]+mk+1,j]+ppxpi i< i<k<i k∈(i,i+1,.j-1) k的位置只有j一种可能 2025年4月3日 26
2025年4月3日 26 建立递归关系 + + + = = − m i k m k j p p p i j i j m i j i k j min { [ , ] [ 1, ] } 0 [ , ] 1 i k j k 的位置只有 j − i 种可能 ◼可以递归地定义m[i,j]为: k∈(i,i+1,.j-1)

2.3.3计算最优值 白东程子太程 HANDONG UNIVERSITY OF TECHNOLOOY 会清合会六会8会的是 对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问 题。因此,不同子问题的个数最多只有 n=⊙(n2) 。 由此可见,在递归计算时,许多子问题被重复计算多 次。这也是该问题可用动态规划算法求解的又一显著 特征。 。 用动态规划算法解此问题,可依据其递归式以自底向 上的方式进行计算。在计算过程中,保存已解决的子 问题答案。每个子问题只计算一次,而在后面需要时 只要简单查一下,从而避免大量的重复计算,最终得 到多项式时间的算法 2025年4月3日 27
2025年4月3日 27 2.3.3计算最优值 ⚫ 对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问 题。因此,不同子问题的个数最多只有 ⚫ 由此可见,在递归计算时,许多子问题被重复计算多 次。这也是该问题可用动态规划算法求解的又一显著 特征。 ⚫ 用动态规划算法解此问题,可依据其递归式以自底向 上的方式进行计算。在计算过程中,保存已解决的子 问题答案。每个子问题只计算一次,而在后面需要时 只要简单查一下,从而避免大量的重复计算,最终得 到多项式时间的算法 ( ) 2 2 n n n + =
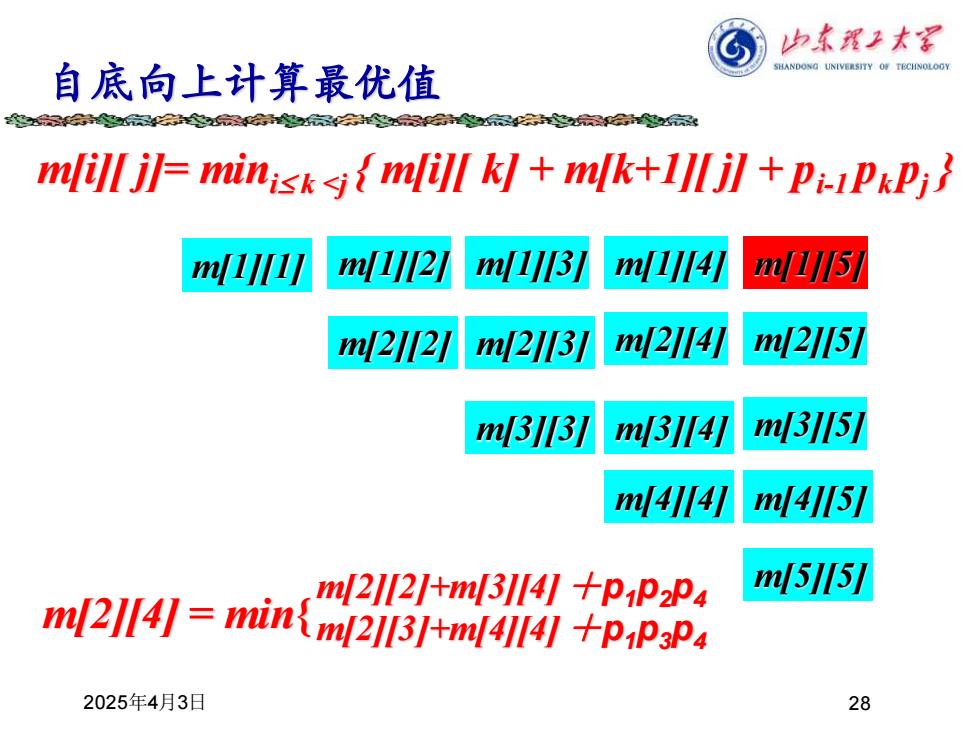
归本程上太军 自底向上计算最优值 SHANDONG UNIVERSITY OF TECINOLOGY mfill jl=minisk{mfill kl+mlk+lljl pi-PkPi m(II m[Il[21 m(I[3] m/I4] 1/5/ ml21121 m[21131 m[21141 mW215/ l33 l3∥4 l3l5/ ml41141 ml41[51 m2l2I+ml3l4十pP2P4 m[51[5] m[21141=min{m/21131+m/41141 +PP3P4 2025年4月3日 28
2025年4月3日 28 自底向上计算最优值 m[i][ j]= mini k <j { m[i][ k] + m[k+1][ j] + pi-1 pk pj } m[1][1] m[1][5] m[4][4] m[5][5] m[2][2] m[3][3] m[4][5] m[3][4] m[2][3] m[1][2] m[1][3] m[2][4] m[3][5] m[1][4] m[2][5] m[2][4] = min{ m[2][2]+m[3][4] +p1p2p4 m[2][3]+m[4][4] +p1p3p4
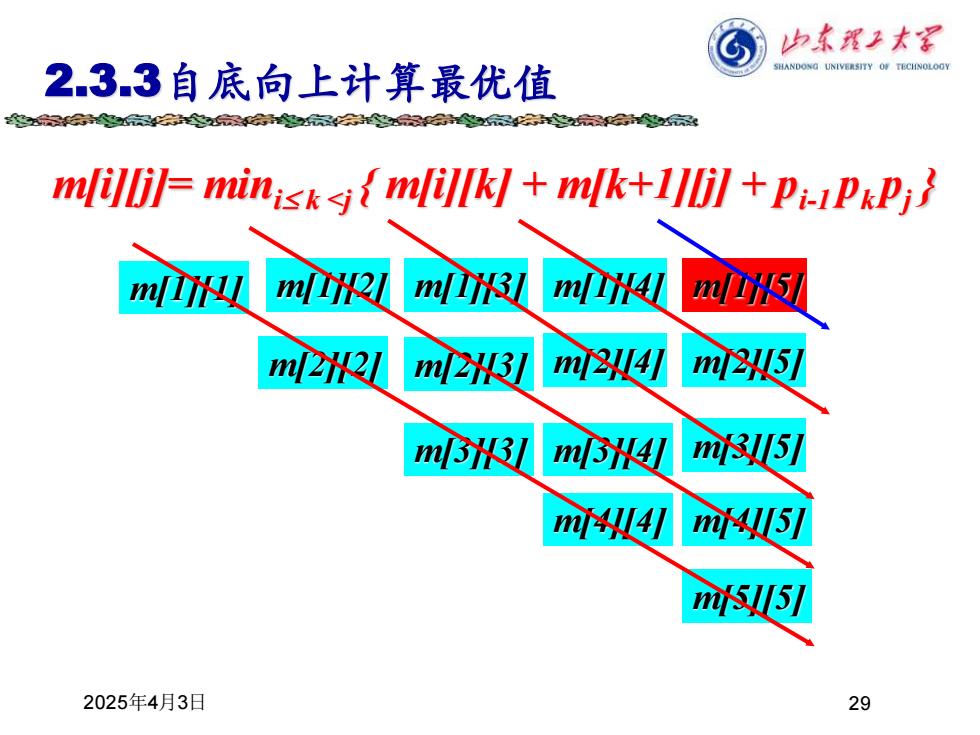
白东程子太军 2.3.3自底向上计算最优值 SHANDONG UNIVERSITY OF TECINOLOGY 会清然是3公3✉ mlillil=minisk{mlillkl mlk+lllil +Pi-PxPi m/义 mti2l mlTi3l m m m2121 m[2431 m火4 m m31331 mB3H441 m35] m义4l mi45] m 2025年4月3日 29
2025年4月3日 29 2.3.3自底向上计算最优值 m[i][j]= mini k <j { m[i][k] + m[k+1][j] + pi-1 pk pj } m[1][1] m[1][5] m[4][4] m[5][5] m[2][2] m[3][3] m[4][5] m[3][4] m[2][3] m[1][2] m[1][3] m[2][4] m[3][5] m[1][4] m[2][5]

归东程子末军 2.3.3自底向上计算最优值 SHANDONG UNIVERSITY OF TECINOLOGY 华器会空空合安会空会的会路 void MatrixChain(int *p,int n,int **m,int **s) { for (int i=1;i<=n;i++)m[i][i]0; for (int r=2;r<=n;r++) 计算第个对角线 for (int i=1;i<=n-r+1;i++){ int j=i+r-1; 体计算m* m0]l=mi+1]]+p[i-1]*p[0*pl: s[i]]=i; for (int k i+1;k<j:k++){int t m[i][k]m[k+1][j]p[i-1]*p[k]*p[] if (t m[i]u]){m[i]l]t;s[=k;)} 获取构造最优解的信息: } S]]记录A[:门的最优 次序的断开位置 2025年4月3日
2025年4月3日 30 2.3.3自底向上计算最优值 void MatrixChain(int *p,int n,int **m,int **s) { for (int i = 1; i <= n; i++) m[i][i] = 0; for (int r = 2; r <= n; r++) /* 计算第r个对角线 */ for (int i = 1; i <= n - r+1; i++) { int j=i+r-1; /* 计算m[i][j] */ m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j]; s[i][j] = i; for (int k = i+1; k < j; k++) {int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;} } } } 获取构造最优解的信息: S[i][j]记录A[i:j]的最优 次序的断开位置k