山东理工大学：《计算机算法设计与分析》课程教学课件（PPT讲稿）第三章 动态规划 Dynamic Programming

归本程子末军 SHANDONG UNIVERSITY OF TECHNOLOOY 华器纹修空条品的深品 ●Catalan数是组合数学中一个常出现在各种计数问 题中出现的数列。由以比利时的数学家欧仁·查 理·卡塔兰（1814-1894)命名。 原理： ● 令h(0)=1,h(1)=1,catalan数满足递归式： ● h(n)=h(0)*h(n-1)+h(1)*h(n-2)+.+h(n- 1)h(0)(其中n>=2) 该递推关系的解为： h(n)=C(2n,n)/(n+1)(n=1,2,3,) 2025年4月3日 21

2025年4月3日 21 ⚫ Catalan数是组合数学中一个常出现在各种计数问 题中出现的数列。由以比利时的数学家欧仁·查 理·卡塔兰 (1814–1894)命名。 ⚫ 原理： ⚫ 令h(0)=1,h(1)＝1,catalan数满足递归式： ⚫ h(n)= h(0)*h(n-1) + h(1)*h(n-2) + . + h(n- 1)h(0) (其中n>=2) ⚫ 该递推关系的解为： ⚫ h(n)=C(2n,n)/(n + 1) (n=1,2,3,.)

归东程子末军 SHANDONG UNIVERSITY OF TECHNOLOGY 2.3求解矩阵连乘问题的动态规划算法 s绿是会空会3分3会深会器会 ●分析最优解的结构； ●递归地定义最优值； ●自底向上地计算出最优值，并获取构造最优解 的信息； ●根据构造最优解的信息构造优化解。 2025年4月3日 22

2025年4月3日 22 2.3求解矩阵连乘问题的动态规划算法 ⚫ 分析最优解的结构； ⚫ 递归地定义最优值； ⚫ 自底向上地计算出最优值，并获取构造最优解 的信息； ⚫ 根据构造最优解的信息构造优化解

白东程子太军 2.3.1分析最优解的结构 SHANDONG UNIVERSITY OF TECINOLOGY 会是3会公☆ ●两个记号 ■A[ij]=AxAi+1X.×Aj ■m[叮]=计算A[ij]的最少乘法次数 ● 最优解的结构 ■若计算A[1:n]的最优顺序在k处断开矩阵链，即 A[1:n]=A[1:k]×A[k+1:n],则在A[1:n]的最优顺序 中，对应于子问题A[1:k]的解必须是A[1:k]的最优解 对应于子问题A[k+1:n]的解必须是A[k+1:n]的最优 解。 具有最优子结钓： 间题的最优解包格子问题的最优解 2025年4月3日 23

2025年4月3日 23 2.3.1 分析最优解的结构 ⚫ 两个记号 ◼ A[i:j]=AiAi+1.Aj ◼ m[i][j]=计算A[i:j]的最少乘法次数 ⚫ 最优解的结构 ◼ 若计算A[1:n]的最优顺序在k处断开矩阵链, 即 A[1:n]=A[1:k]A[k+1:n]，则在A[1:n]的最优顺序 中，对应于子问题A[1:k]的解必须是A[1:k]的最优解， 对应于子问题A[k+1:n]的解必须是A[k+1:n]的最优 解。 具有最优子结构： 问题的最优解包括子问题的最优解

归本程子末军 2.3.1分析最优解的结构 SHANDONG UNIVERSITY OF TECINOLOGY 会会是会S会会 ●子问题重叠性 AXA2XA3XA (A)x(A2XA3XA (A×A2)X(A3×A4) (AA2×A3)x(A4) (A2xA) (A3×A) (A×A2) (A3×A) (A×Az) (AxA:) 具有子问题重叠性 2025年4月3日 24

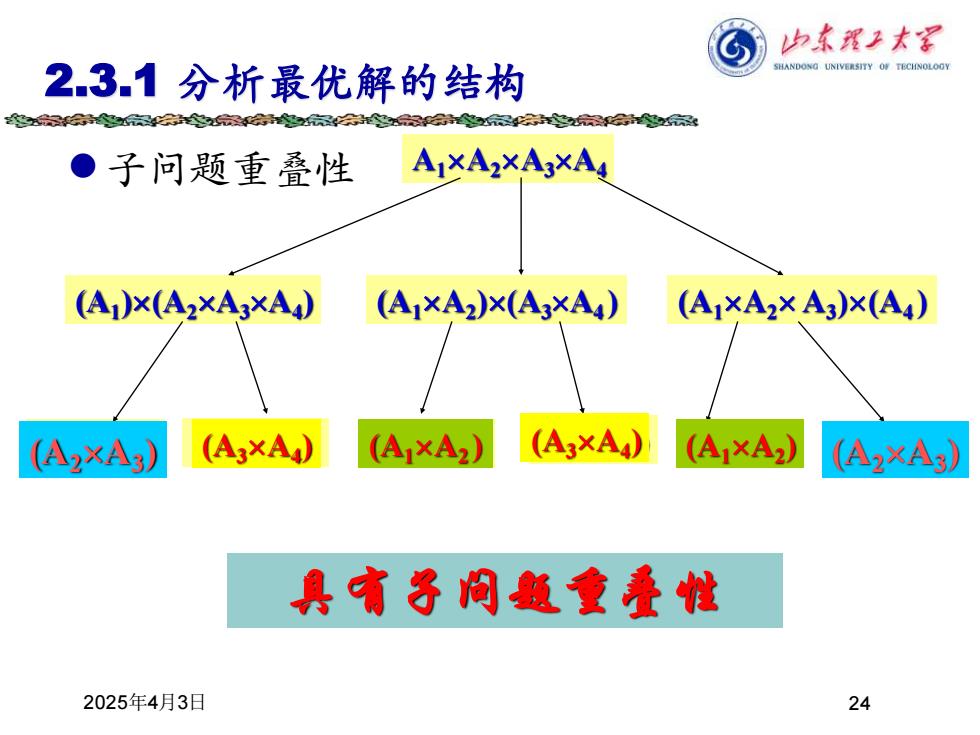
2025年4月3日 24 2.3.1 分析最优解的结构 ⚫子问题重叠性 A1A2A3A4 (A1 )(A2A3A4 ) (A1A2 )(A3A4 ) (A1A2 A3 )(A4 ) (A2A3) (A3 A4) (A1A2 ) (A2A3 ) (A3A4 (A ) 1 A2 (A ) 3A4 ) (A3A4 (A ) 1A2 ) (A1A2 ) 具有子问题重叠性 (A2A3 ) (A2A3 )

白东程子太军 2.3.2递归地定义最优值 SHANDONG UNIVERSITY OF TECINOLOGY 8会清合会的品冷空3品会是 ●假设 ■mll=计算A[i:j的最小乘法数 ■设(AAk)（Ak+1.A)是最优化解(k实际上是 不可预知 考虑到所有的k,最优值的递归方程为： m[ill j]=0 if i-j m[ill jl=minisksi{mlill k]+m[k+1][jl+pi Pk Pi}if i<j 其中，PPP;是计算A:k×Ak+1l所需乘法 数，A[i:k和A[k+1:j分别是pP和pkP矩阵. 这里A的维数为P-1×P 2025年4月3日 25

2025年4月3日 25 2.3.2递归地定义最优值 ⚫ 假设 ◼m[i][j]=计算A[i:j]的最小乘法数 ◼设（Ai .Ak）（Ak+1 .Aj )是最优化解(k实际上是 不可预知) 考虑到所有的k，最优值的递归方程为： m[i][ j]= 0 if i=j m[i][ j]= minik<j{ m[i][ k]+m[k+1][ j]+pi-1 pk pj } if i<j 其 中 , pi-1pkpj 是计算 A[i:k]A[k+1:j] 所需乘法 数,A[i:k]和A[k+1:j]分别是pi-1pk和pkpj矩阵. 这里 Ai 的维数为 pi−1  pi