
3.单位Jnits:压力的单位最多 有Pa、atm、kgf/cm(at)、mmHg、mH,0、bar等,它们之间的换算关系为: 1atm=101325Pa=1.01325bar =1.0332kgf/cm2(at)=10.332mH,0=760mmHg 1kgf/cm2(at)=10mH,O=735.56mmHg =9.807x104Pa=0.9807bar=0.9678atm 生基准Datum (1)绝对压力和表压:绝对压力以零压力(绝对真空)为基准,表压则以当地大气压为基准 测定压力 绝 当地大气压(表压为零) 力 业压 零压力、绝对真空(绝对压力为零 所以表压=绝对压力大气压 (2)真空度:真空度也以当地大气压为基准,但真空度与表压的计算方向相反,即低于大气压的 数值称为真空度 当地大气压(真空度为零)(表压为零) 大 测定压力 零压力、绝对真空(绝对压力为零) 所以 真空度=大气压-绝对压力 表压=一真空度
3. 单位Units:压力的单位最多 有Pa、atm、kgf/cm2 (at)、mmHg、mH2O、bar等,它们之间的换算关系为: 1atm=101325Pa=1.01325bar =1.0332kgf/cm2 (at)=10.332mH2O=760mmHg 1kgf/cm2 (at)=10mH2O=735.56mmHg =9.807104Pa=0.9807bar=0.9678atm 4. 基准Datum (1)绝对压力和表压:绝对压力以零压力(绝对真空)为基准,表压则以当地大气压为基准 测定压力 当地大气压(表压为零) 零压力、绝对真空(绝对压力为零 所以 表压=绝对压力-大气压 (2)真空度:真空度也以当地大气压为基准,但真空度与表压的计算方向相反,即低于大气压的 数值称为真空度 当地大气压(真空度为零)(表压为零) 测定压力 零压力、绝对真空(绝对压力为零) 所以 真空度 = 大气压-绝对压力 表压=-真空度 绝 对 压 力 表 压 大 气 压 大 气 压 真 空 度 绝 对 压 力
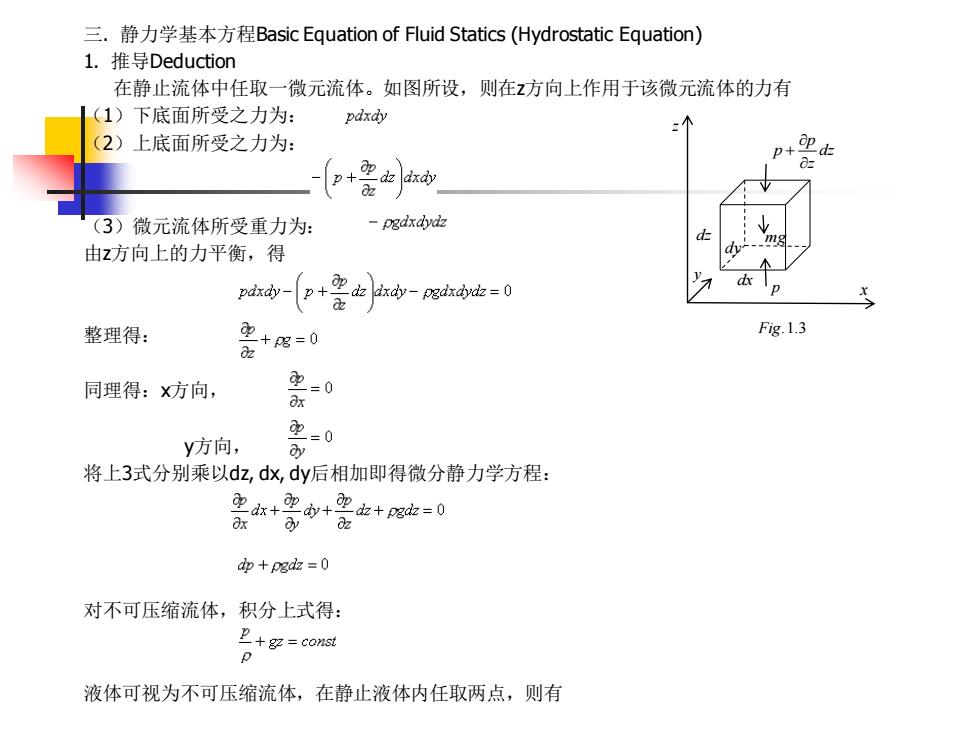
三.静力学基本方程Basic Equation of Fluid Statics(Hydrostatic Equation) 1.推导Deduction 在静止流体中任取一微元流体。如图所设,则在z方向上作用于该微元流体的力有 (1)下底面所受之力为: pdxdy (2)上底面所受之力为: p+pd p+ dz drdy (3)微元流体所受重力为: -pgdxdydz 由z方向上的力平衡,得 1 pdxdy- o, p+ -dz2ry-pgdxdyd边=0 整理得: 电+g=0 Fig.1.3 同理得:方向, 2-0 8x y方向, 2-0 y 将上3式分别乘以dz,dx,dy后相加即得微分静力学方程: 、+四y+2+8三0 dp+pgdz =0 对不可压缩流体,积分上式得: g=comst p 液体可视为不可压缩流体,在静止液体内任取两点,则有
三. 静力学基本方程Basic Equation of Fluid Statics (Hydrostatic Equation) 1. 推导Deduction 在静止流体中任取一微元流体。如图所设,则在z方向上作用于该微元流体的力有 (1)下底面所受之力为: (2)上底面所受之力为: (3)微元流体所受重力为: 由z方向上的力平衡,得 整理得: 同理得:x方向, y方向, 将上3式分别乘以dz, dx, dy后相加即得微分静力学方程: 对不可压缩流体,积分上式得: 液体可视为不可压缩流体,在静止液体内任取两点,则有 dz z p p + p dx dy dz x z y Fig.1.3 mg

L+g1=2+8 或 P2=P1+Pg31-22) h=Z1-22 则得液体静力学基本方程: P2=p1+Pg的 结陀Conclusions (1)在静止连续的同一液体内,水平面必为等压面。 (2)静止液体内任何一点压力的变化,将传至液体内的所有各点。 (3)可以用液柱高度来表示压力差或压力。 由 P2=p1+pgh 得 h=P-凸 唱 当 P1=0,P2=p 时 得 h=卫 g 上两式说明压力差或压力与一定液体的液柱高度一一对应。 由于气体的密度随高度的变化甚微,所以液体静力学方程在高度不大时也适用于气体。 3.气压方程Barometric equation 将理想气体状态方程 代入 迎+pgz=0 得 迎+84z=0 p RT
或 令 则得液体静力学基本方程: 2. 结论Conclusions (1) 在静止连续的同一液体内,水平面必为等压面。 (2) 静止液体内任何一点压力的变化,将传至液体内的所有各点。 (3) 可以用液柱高度来表示压力差或压力。 由 得 当 时 得 上两式说明压力差或压力与一定液体的液柱高度一一对应。 由于气体的密度随高度的变化甚微,所以液体静力学方程在高度不大时也适用于气体。 3. 气压方程Barometric equation 将理想气体状态方程 代入 得