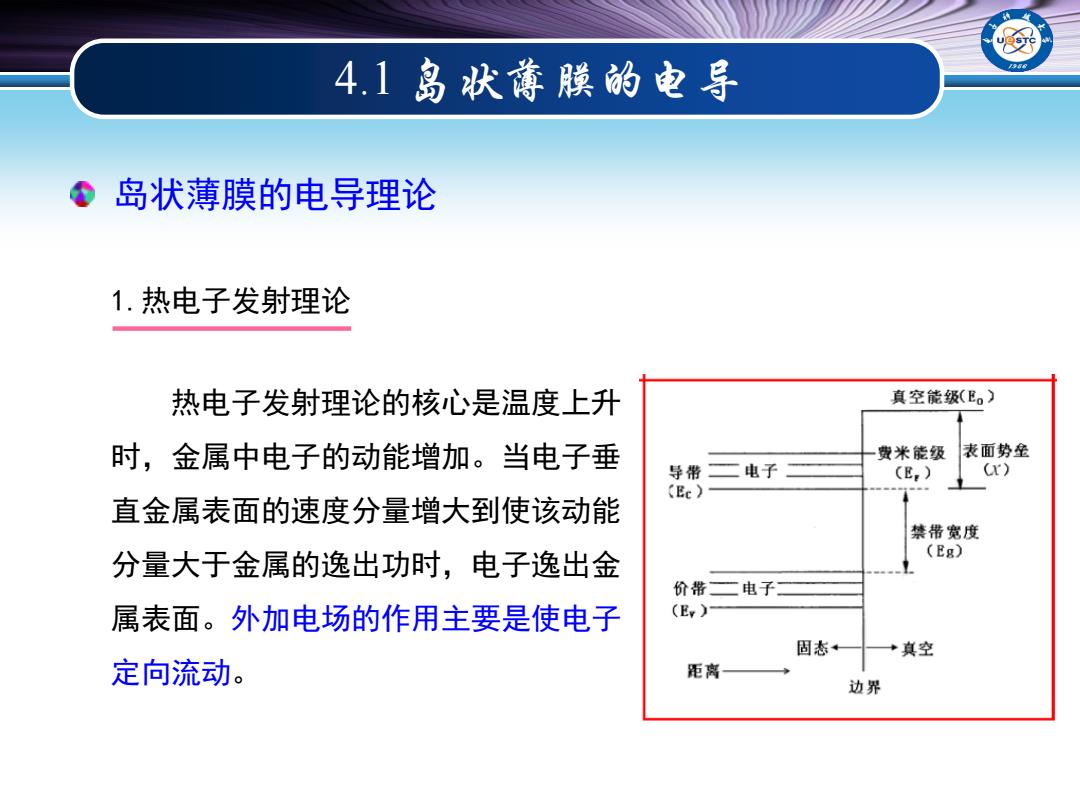
4.1岛次薄膜的电导 岛状薄膜的电导理论 1.热电子发射理论 热电子发射理论的核心是温度上升 真空能级(E。) 时,金属中电子的动能增加。当电子垂 费米能级 表面势垒 导带二 电子 (E,) ( cEc) 直金属表面的速度分量增大到使该动能 禁带宽度 分量大于金属的逸出功时,电子逸出金 (Eg) 价带二电子 属表面。外加电场的作用主要是使电子 (E,) 固态←一 →真空 定向流动。 距离 边界
4.1 岛状薄膜的电导 热电子发射理论的核心是温度上升 时,金属中电子的动能增加。当电子垂 直金属表面的速度分量增大到使该动能 分量大于金属的逸出功时,电子逸出金 属表面。外加电场的作用主要是使电子 定向流动。 岛状薄膜的电导理论 1.热电子发射理论

4.1岛状薄膜的电导 假设电子的位能在表面发生突变,温度为时,在金属中向 表面运动的一个电子的速度分量分别为Vx、.', 假设V为垂 直金属表面的速度分量,则电子逸出金属的条件是: (4-1) 式中m是电子的有效质量。 热电子发射的电流密度可由对单位时间内到 达单位表面的,能量具备逸出条件的电子数计 算获得。 Eo
4.1 岛状薄膜的电导 2 2 2 1 2 1 2 3 m m x k T 式中m是电子的有效质量。 热电子发射的电流密度可由对单位时间内到 达单位表面的,能量具备逸出条件的电子数计 算获得。 (4-1) 假设电子的位能在表面发生突变,温度为T时,在金属中向 表面运动的一个电子的速度分量分别为Vx、Vy、 Vz,假设Vx为垂 直金属表面的速度分量,则电子逸出金属的条件是:
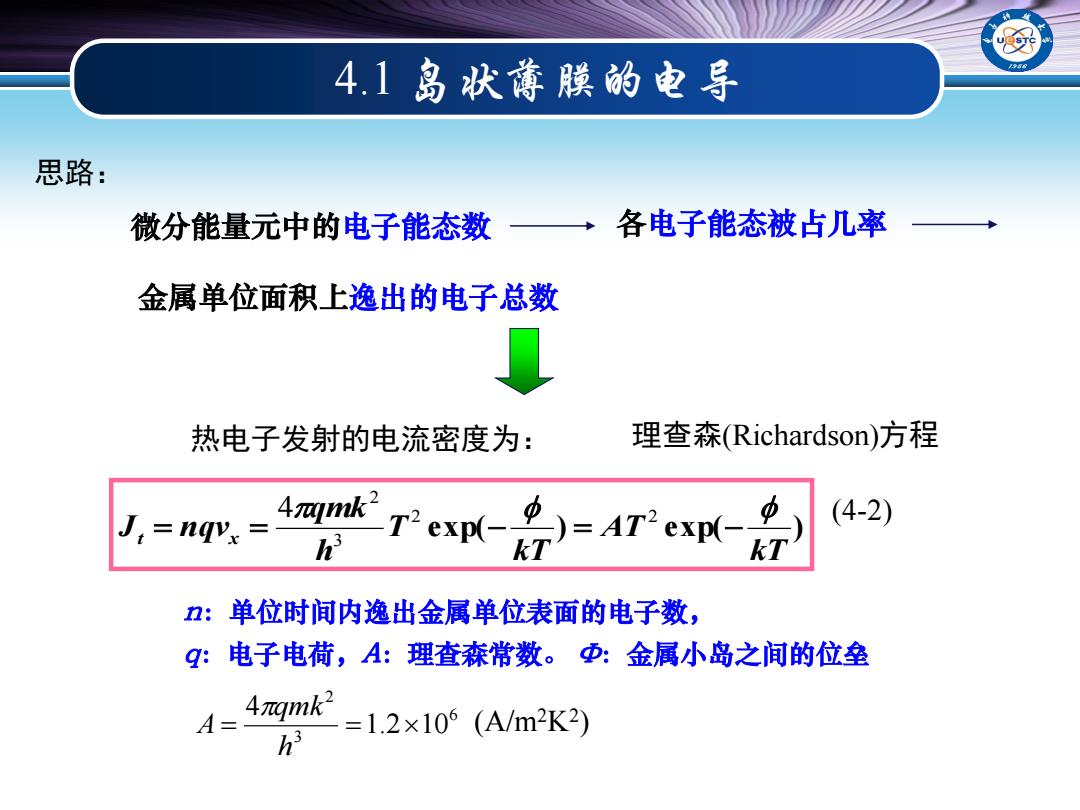
4.1岛次薄膜的电导 思路: 微分能量元中的电子能态数一→各电子能态被占几率 金属单位面积上逸出的电子总数 热电子发射的电流密度为: 理查森(Richardson)方程 J,=ngv.= Te-导=r产e (4-2) h kT n:单位时间内逸出金属单位表面的电子数, q:电子电荷,A:理查森常数。Φ:金属小岛之间的位垒 4mk=-1.2x10(A/m2K2) 3
4.1 岛状薄膜的电导 exp( ) exp( ) kT AT kT T h qmk J nqv t x 2 2 3 2 4 热电子发射的电流密度为: (4-2) n:单位时间内逸出金属单位表面的电子数, q:电子电荷,A:理查森常数。 Φ:金属小岛之间的位垒 6 3 2 1.2 10 4 h qmk A (A/m2K2 ) 微分能量元中的电子能态数 各电子能态被占几率 金属单位面积上逸出的电子总数 思路: 理查森(Richardson)方程

4.1岛状薄膜的电导 4mTcw爱)=T产e(-岩=gq,r=d1w 0,=1 m 3k ng'r ngv d T个,J1,p 得出:电导温度系数为正,电阻温度系数为负 该理论的缺陷:①未引入外加电场的影响;无F-p关系; ②电流密度未考虑小岛尺寸的影响, 电阻率与小岛尺寸的关系与实际相反; ③位垒高度却比实验值大1~2个数量级,计算出的 电流密度远小于实际值(相差几个数量级)。 该理论只能近似应用于高温、低位垒和大距离岛间距的情况
4.1 岛状薄膜的电导 该理论的缺陷:① 未引入外加电场的影响;无F -ρ关系; ② 电流密度未考虑小岛尺寸的影响, 电阻率与小岛尺寸的关系与实际相反; ③位垒高度却比实验值大1~2个数量级,计算出的 电流密度远小于实际值(相差几个数量级)。 该理论只能近似应用于高温、低位垒和大距离岛间距的情况。 得出:电导温度系数为正,电阻温度系数为负 nqv d v kT AT kT T h qmk Jt exp( ) exp( ) / 3 2 2 , 2 4 T↑,Jt↑,ρ↓ exp( ) m q d kT kT h nqv d mv nq m x x t 2 2 3 2 4 1 3

4.1岛次薄膜的电导 2.肖特基发射理论(理查森一肖特基理论) 以热电子发射理论的为基础; 考虑到:1、电子脱离小岛需克服的势垒是渐变的,非突变的; 2、热电子发射理论所得到的电流密度太小; 在电子逸出金属小岛表面所需要克服的位垒中,引入境像力和外加 电场的影响。 位垒降低 电流密度计算值增加
4.1 岛状薄膜的电导 在电子逸出金属小岛表面所需要克服的位垒中,引入境像力和外加 电场的影响。 2.肖特基发射理论(理查森—肖特基理论) 以热电子发射理论的为基础; 位垒降低 电流密度计算值增加 考虑到:1、电子脱离小岛需克服的势垒是渐变的,非突变的; 2、热电子发射理论所得到的电流密度太小;