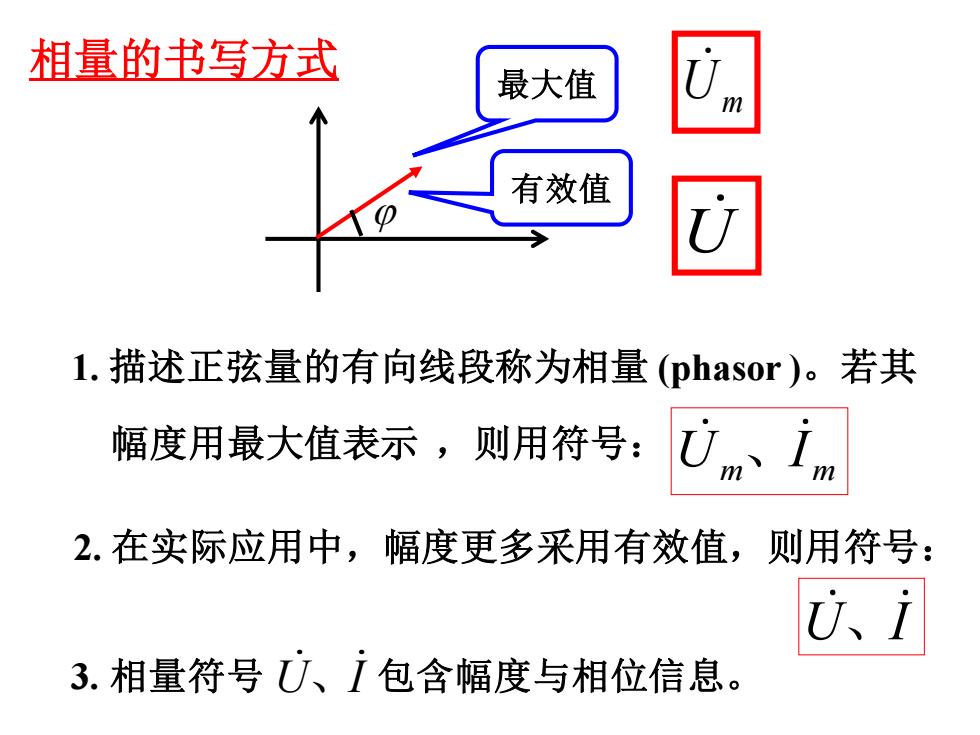
相量的书写方式 最大值 有效值 1.描述正弦量的有向线段称为相量(phasor)。若其 幅度用最大值表示,则用符号: Un、im 2.在实际应用中,幅度更多采用有效值,则用符号: u、i 3.相量符号U、包含幅度与相位信息
U I 3. 相量符号 、 包含幅度与相位信息。 有效值 1. 描述正弦量的有向线段称为相量 (phasor )。若其 幅度用最大值表示 ,则用符号: m m U I 、 Um U 相量的书写方式 最大值 2. 在实际应用中,幅度更多采用有效值,则用符号: U I
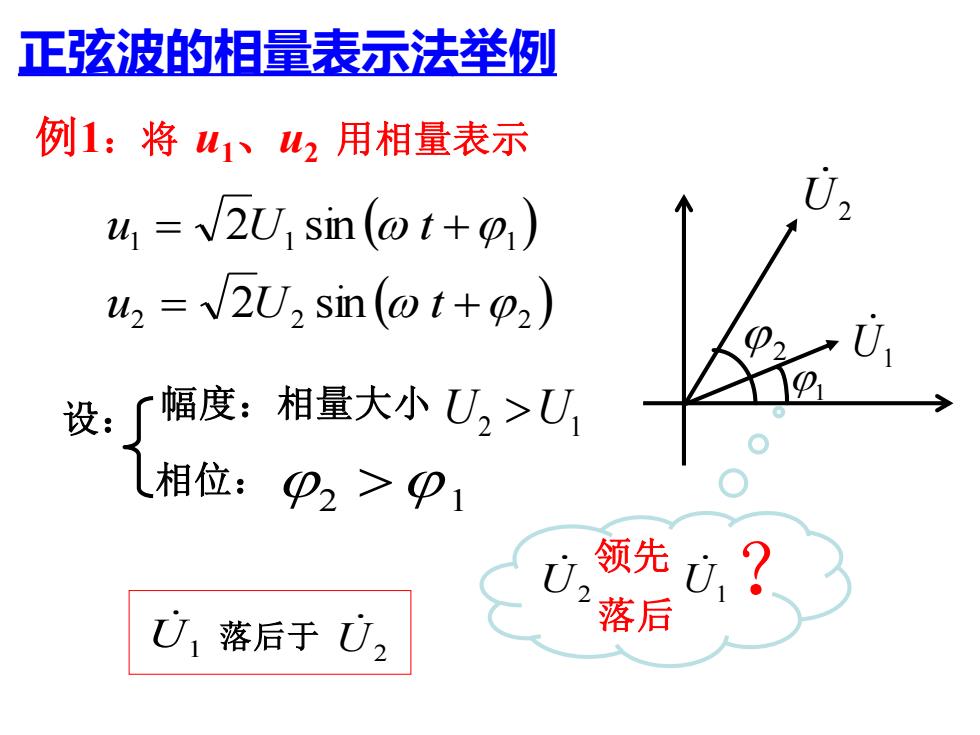
正弦波的相量表示法举例 例1:将u12用相量表示 u v2U sin (@t+p) uz J2U2 sin (t+o2) (0 设:了幅度:相量大小U2>U 相位:P2>P1 0. 领先ù,? U 落后于U2 落
( ) ( ) 2 2 2 1 1 1 2 sin 2 sin = + = + u U t u U t U1 1 U2 2 U2 落后于 U1 U1 U2 领先 落后 ? 正弦波的相量表示法举例 例1:将 u1、u2 用相量表示 相位: 幅度:相量大小 U2 U1 2 1 设:
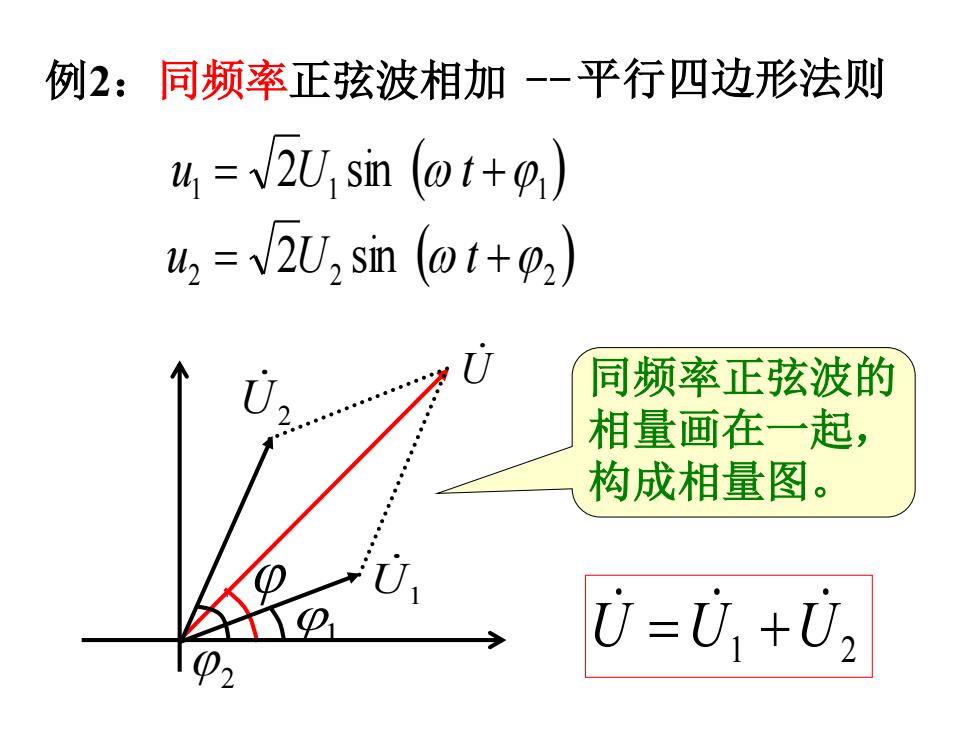
例2:同频率正弦波相加-平行四边形法则 4=2U,sn(@t+0,) 4,=v2U2sn(ot+p2) 同频率正弦波的 相量画在一起, 构成相量图。 0=U+U
U U1 U2 = + U ( ) ( ) 2 2 2 1 1 1 2 sin 2 sin = + = + u U t u U t 同频率正弦波的 相量画在一起, 构成相量图。 例2:同频率正弦波相加 -平行四边形法则 2 U2 U1 1
注意 1.只有正弦量才能用相量表示,非正弦量不可以。 2.只有同频率的正弦量才能画在一张相量图上, 不同频率不行。 新问题提出: 平行四边形法则可以用于相量运算,但不方便。 故引入相量的复数运算法。 相量一→复数表示法→复数运算
注意 : 1. 只有正弦量才能用相量表示,非正弦量不可以。 2. 只有同频率的正弦量才能画在一张相量图上, 不同频率不行。 新问题提出: 平行四边形法则可以用于相量运算,但不方便。 故引入相量的复数运算法。 相量 复数表示法 复数运算
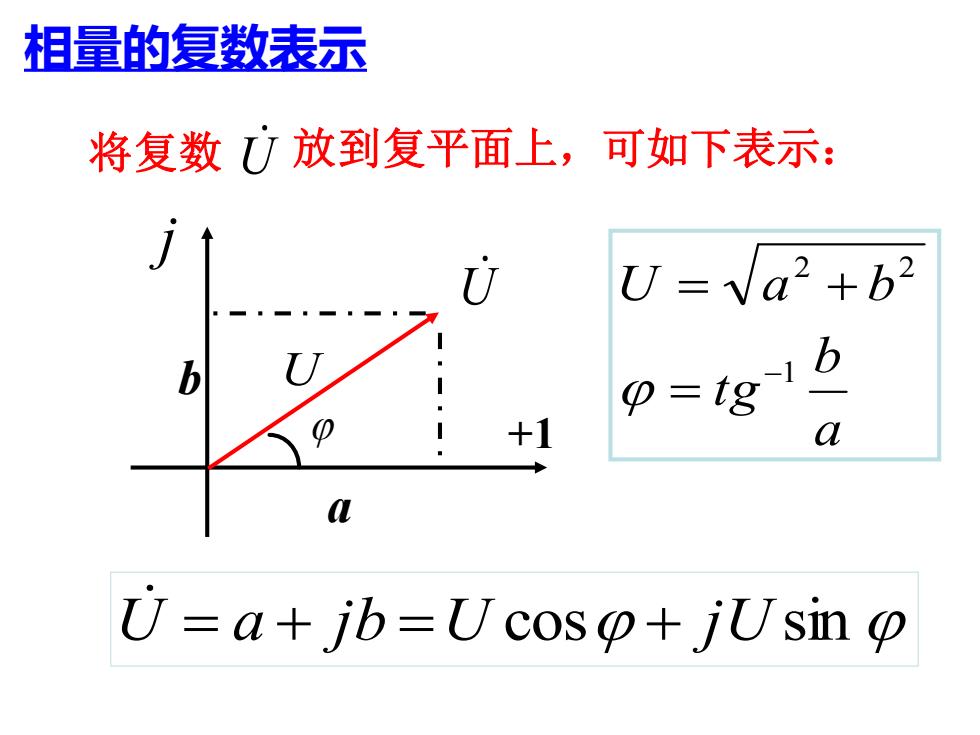
相量的复数表示 将复数)放到复平面上,可如下表示: U=Va2+b2 b o=tg +1 a U=a+jb=Ucosp+jUsin p
U = a + j b =U cos + j U sin 相量的复数表示 a b U U j +1 将复数 U 放到复平面上,可如下表示: a b t g U a b 1 2 2 − = = +