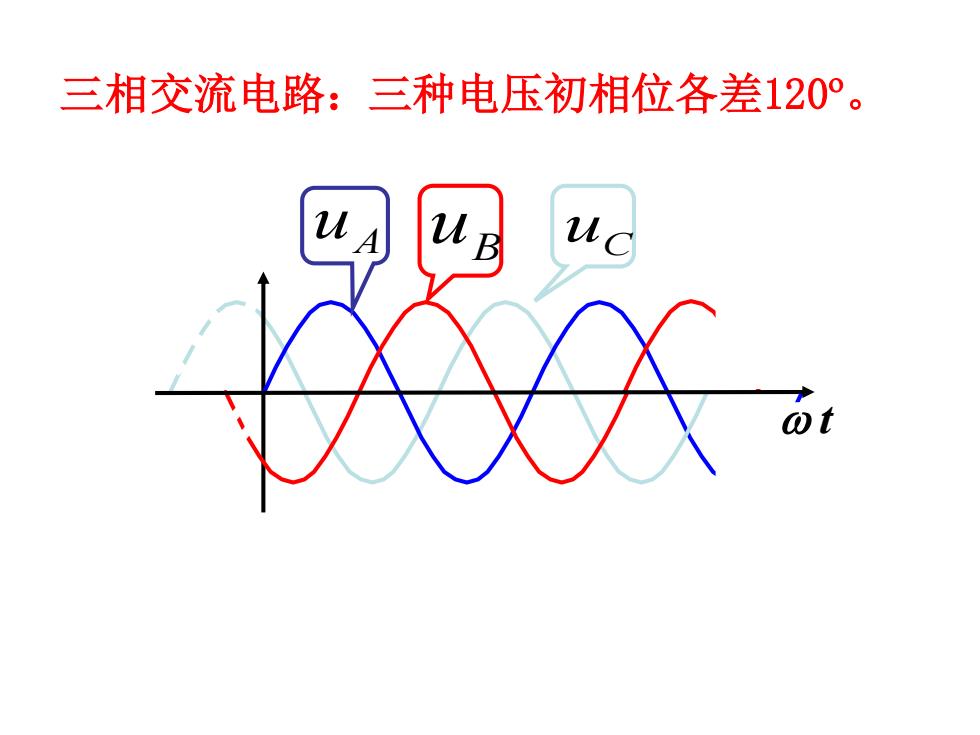
三相交流电路:三种电压初相位各差120°
三相交流电路:三种电压初相位各差120 。 A uB uC u t

可以证明同频率正弦波运算后,频率不变。 如:∫4,=V2U1sin(ot+0,)》 Lu2=√2U2sin(wt+p2) u =u +u2 =2Uin (@t+)+22 sin (@t+2) -2Usin (@t+o) 幅度、相位变化 频率不变 结论: 因角频率(0)不变,所以以下讨论同频率正弦波 时,ω可不考虑,主要研究幅度与初相位的变化
可以证明同频率正弦波运算后,频率不变。 ( ) ( ) 2 2 2 1 1 1 2 sin 2 sin = + = + u U t u U t 如: 结论: 因角频率()不变,所以以下讨论同频率正弦波 时, 可不考虑,主要研究幅度与初相位的变化。 ( ) ( ) ( ) = + = + + + = + U t U t U t u u u 2 sin 2 sin 2 sin 1 1 2 2 1 2 幅度、相位变化 频率不变

例 己知:i=sin(1000t+30°) 幅度: 1-1A1= 等=0701公 频率: @=1000 rad/s 1000 f= =159Hz 2元 2π 初相位: p=30°
例 幅度: 0.707A 2 1 I m =1A I = = 已知: i = sin(1000t +30) 159 Hz 2 1000 2 1000 rad/s = = = = f 频率: 初相位: = 30
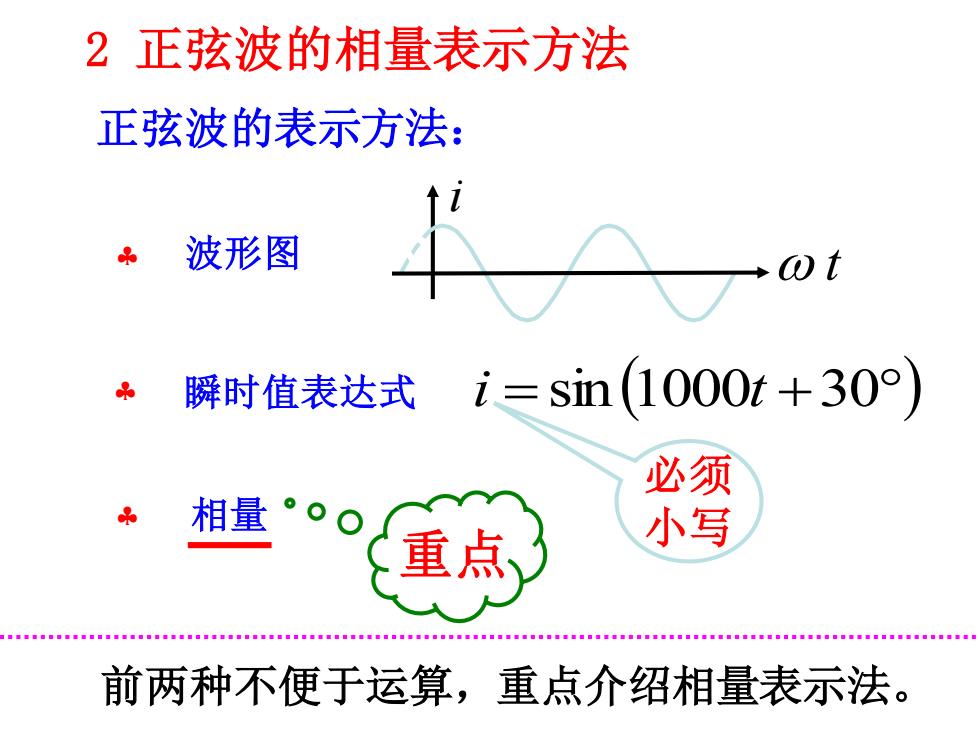
2正弦波的相量表示方法 正弦波的表示方法: 波形图 .ωt 。瞬时值表达式 i=sin(1000t+30°) 必须 相量°o 重点、 小写 前两种不便于运算,重点介绍相量表示法
2 正弦波的相量表示方法 瞬时值表达式 i = sin(1000t +30) 相量 必须 小写 前两种不便于运算,重点介绍相量表示法。 波形图 i t 正弦波的表示方法: 重点
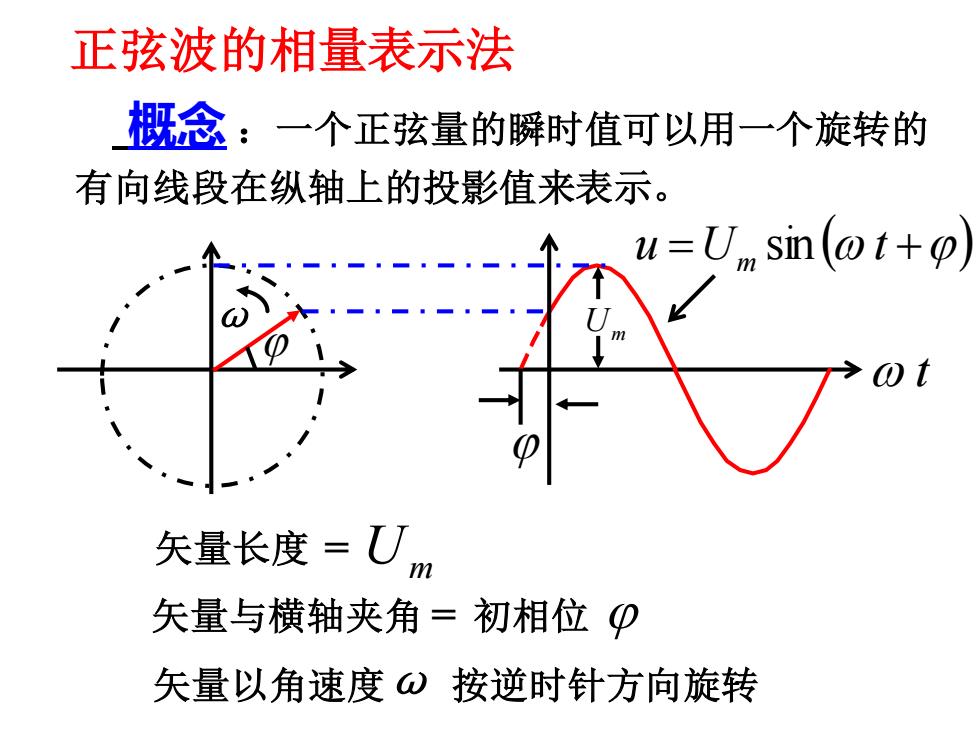
正弦波的相量表示法 概念:一个正弦量的瞬时值可以用一个旋转的 有向线段在纵轴上的投影值来表示。 u=U sin(@t+o 矢量长度=J 矢量与横轴夹角=初相位0 矢量以角速度⊙按逆时针方向旋转
概念 :一个正弦量的瞬时值可以用一个旋转的 有向线段在纵轴上的投影值来表示。 正弦波的相量表示法 矢量长度 = Um 矢量与横轴夹角 = 初相位 矢量以角速度ω 按逆时针方向旋转 u =U ( t +) m sin Um t ω