
)特殊矩阵的压缩存储 ◆对称矩阵 0 a01 a0(n-1) 210 811 a1(-1) 4(n-1)0 a(-1)川 .。 a(-l0 按行序为主序: aoo aio al az0 a21 . a(m-1)0 . a(n-1)(n-1) 元素的位序:k=0 1234 n(n-1)/2 n(n+1)/2-1 前行存储元素的总数为?+)-少 n=
1) 特殊矩阵的压缩存储 u对称矩阵 a00 a01 . . . a0(n-1) a10 a11 . . . a(n-1)0 . a(n-1)(n-1) . . . . . . . . a00 a10 a11 a20 a21 . a(n-1)0 . a(n-1)(n -1) 元素的位序: k = 0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 2 ( 1) ( 1) 1 0 i i p i p

1)当i>j时,在下三角中,a是第(i+1)行第(j+1)列的元素。 a之前有行元素,共有∑(p+1)=近+ 2个: 在第(i+1)行上,a之前有j个元素。 aoo ao1 . a0(-1) a10 a11 .(-1) k=0+) a(m-l00aa-1)1.a(m-1m-1 2 2)当iK时,在上三角中,ⅰ台j即可得到结果。 k=U+1) 2 令I=maxi,j},J=min{i,j},则 k=1(1+D)+J 2 .Loc(a;)=Loc(a[k])=Loc(a[O])+kxd
a00 a01 . . a0(n-1) a10 a11 . . a(n-1)0 . a(n-1)(n-1) . . . . . . 1)当i>=j时,在下三角中,aij是第(i+1)行第(j+1)列的元素。 2 ( 1) ( 1) 1 0 i i p i p j i i k 2 ( 1) 2)当i<j时,在上三角中 i j j k 2 ( 1) J I I k 2 ( 1) Loc(aij) Loc(a[k]) Loc(a[0]) k d j ,i j 即可得到结果
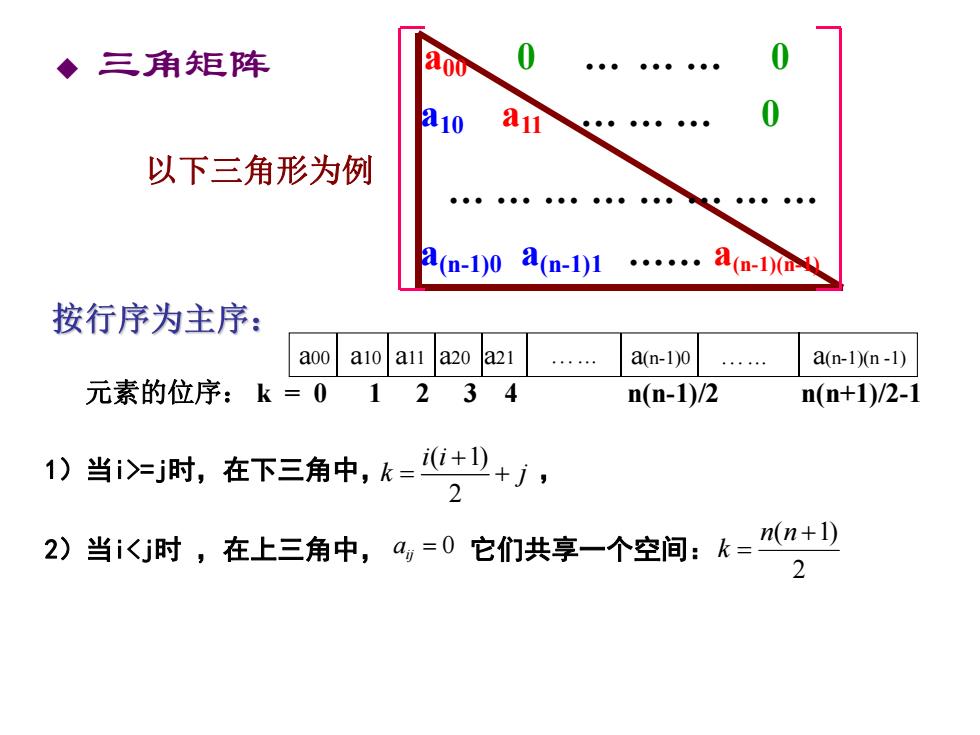
◆三角矩阵 a10 以下三角形为例 a(n-1)0 a(n-1)1 a(m-10 按行序为主序: a00 aio al a20 a21 a(n-1)0 . a(n-1)n-l) 元素的位序:k=01234 n(n-1)/2 n(n+1)/2-1 1) 当1>j时,在下三角中,k=+D+j, 2 2) 当i心j时,在上三角中,a,=0它们共享一个空间:k=n+少 2
u 三角矩阵 以下三角形为例 a00 0 . . . 0 a10 a11 . . . 0 a(n-1)0 a(n-1)1 . a(n-1)(n-1) . . . . . . . . a00 a10 a11 a20 a21 . a(n-1)0 . a(n-1)(n -1) 元素的位序: k = 0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 1)当i>=j时,在下三角中, , 2)当i<j时 ,在上三角中, a ij 0 它们共享一个空间: 2 ( 1) n n k ( 1) 2 i i k j
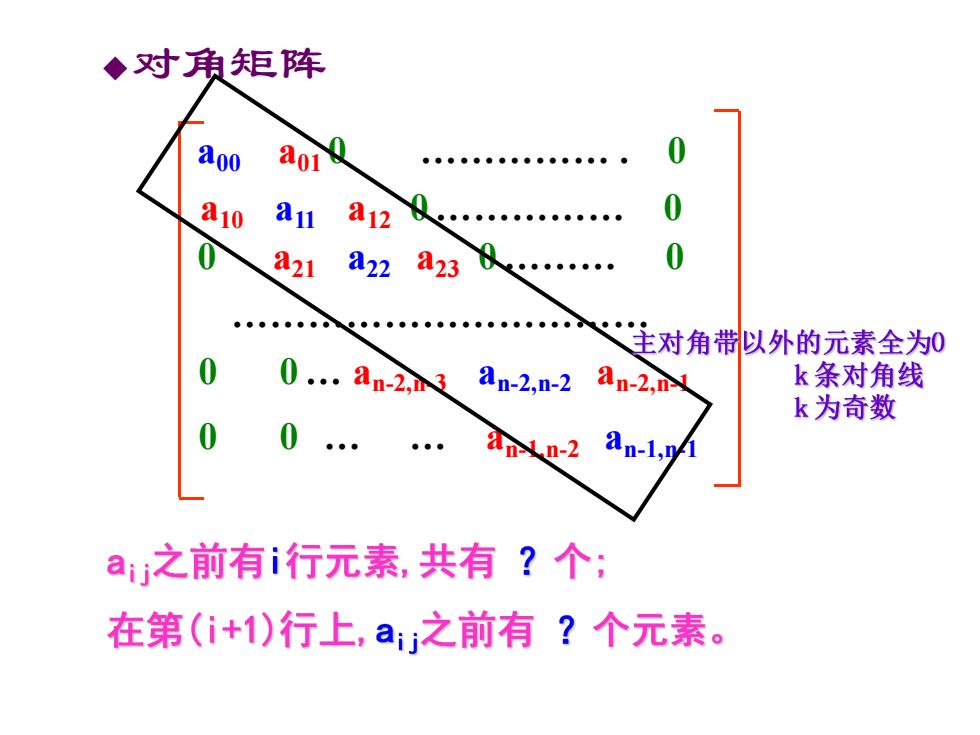
◆对角矩阵 a00 a01 810 a11 a12 ●●●●● 0 821 A22 823 主对角带以外的元素全为0 0.an-2,3 an-2.n-2 an-2,n k条对角线 k为奇数 n-2 an-1, a之前有i行元素,共有?个: 在第(i+1)行上,a之前有?个元素
u对角矩阵 a00 a01 0 . . 0 a10 a11 a12 0. 0 0 0. an-2,n-3 an-2,n-2 an-2,n-1 0 0 . . an-1,n-2 an-1,n-1 0 a21 a22 a23 0. 0

a之前共有i行,共?个元素, 当i=0时,0个; 当n>i>0时,3i-1个。∥每行3个元素,第1行2个 在第(i+1)行上,a之前有?个元素。 当i=0时,j个; 当n>i>0时,(j-i)+1个。∥a-1),ai,a+ k=1,当=0时 2i+j,当n>i>0时 ∴.Loc(a)=Loc(a[k])=Loc(a0])+k×d
当i=0时,0个; 当n>i>0时,3i-1个。// 每行3个元素,第1行2个 当i=0时,j个; 当n>i>0时,(j-i)+1个。// ( 1) ( 1) , , ai i aii ai i , 0 2 , 0 j i k i j n i 当 时 当 时 Loc(aij) Loc(a[k]) Loc(a[0]) k d