电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》课程教学资源（课件讲稿）第6讲 网络函数拓扑法

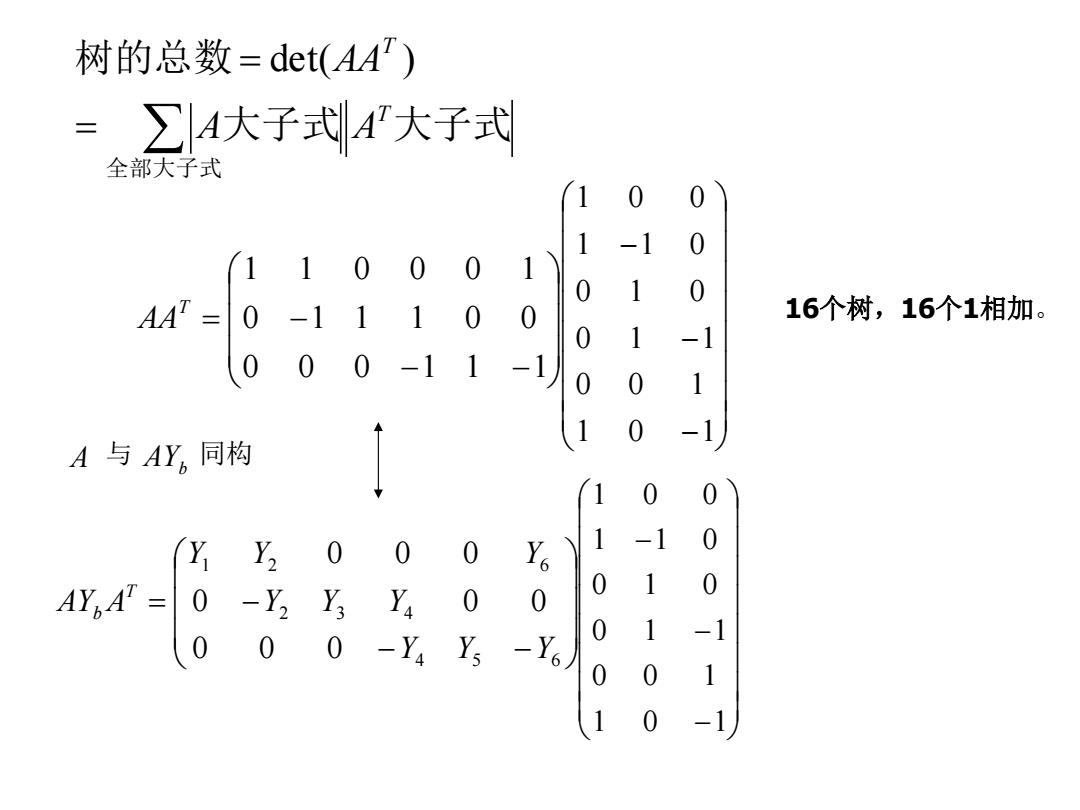
树的总数=det(AAT) = ∑A大子式A大子式 全部大子式 1 110 001Y 0 AA" 0-11 00 16个树，16个1相加。 0 -1 000-11-1 0 A与AY,同构 5 Y 0 0 0 Yo 1 0 AY,AT=0-Y2 0 Y3 Ya 0 0 0 00-Y4 Ys -Yo) 0 0 0 1 1 0 -1

              0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 T AA                        1 0 1 0 0 1 0 1 1 0 1 0 1 1 0 1 0 0 16个树，16个1相加。    全部大子式 大子式 大子式 树的总数 T T A A det(AA )               4 5 6 2 3 4 1 2 6 0 0 0 0 0 0 0 0 0 Y Y Y Y Y Y Y Y Y AY A T b A 与 AYb 同构                        1 0 1 0 0 1 0 1 1 0 1 0 1 1 0 1 0 0

AT是A的转置，非奇异(N-1)阶子阵必对应于 图G的同一树。因此，AT、A对应的大子式 必同为+1或-1，故： det AY4=>det(AY(4') det AYA"=>det(-AY)(-A) 1、△的拓扑求解 △=det Ar.A'=)Ty)=>树支导纳积 (3-4-8) 全部树 全部树

AT是A的转置，非奇异(N-1)阶子阵必对应于 图G的同一树。因此， AT 、A对应的大子式 必同为+1或-1，故： （ ）（ ） （ ） T b T b T b T b AY A AY A AY A AY A       det det det det ( )       全部树 全部树 det AYb A T T(y) 树支导纳积 1、△的拓扑求解 （3-4-8）