二叉树(Binary Tree) .二叉树的定义 一棵二叉树是结点的一个有限集合,该集合 或者为空,或者是由一个根结点加上两棵分 别称为左子树和右子树的、互不相交的二叉 树组成。 ☑ R 二叉树的五种不同形态 11
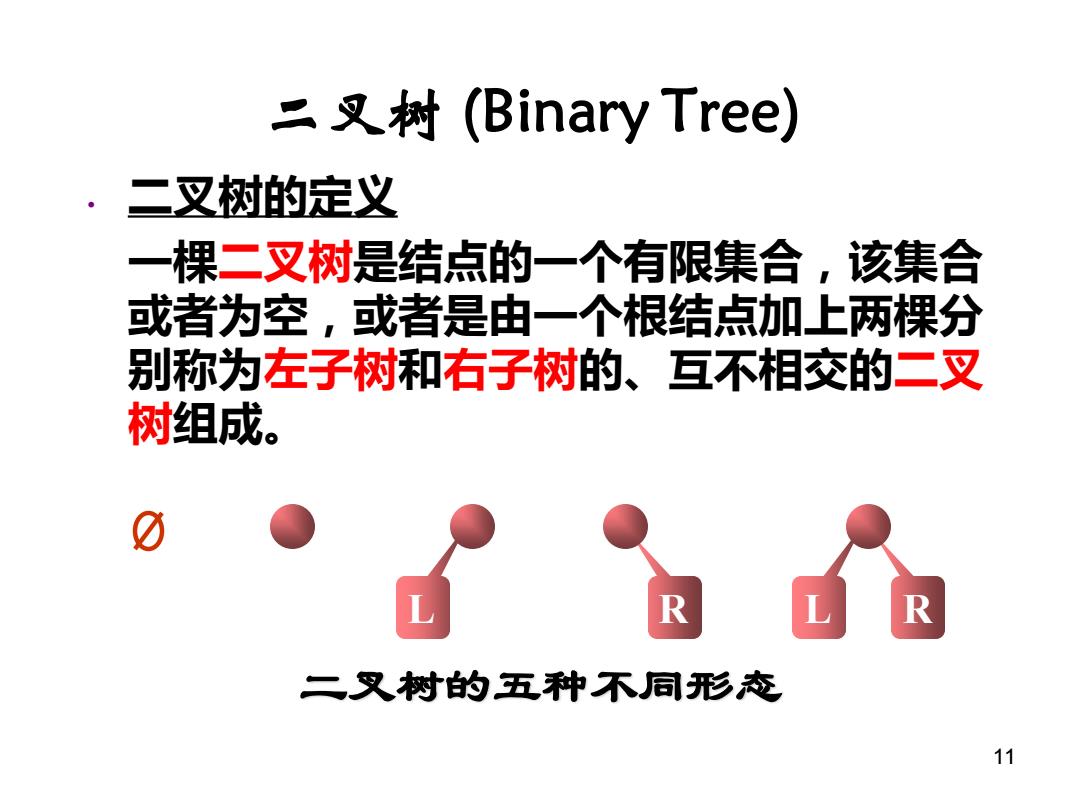
二叉树的五种不同形态 L R L R 二叉树 (Binary Tree) • 二叉树的定义 一棵二叉树是结点的一个有限集合,该集合 或者为空,或者是由一个根结点加上两棵分 别称为左子树和右子树的、互不相交的二叉 树组成。 11

二叉树的性质 ·性质1若二叉树结点的层次从1开始,则在 二叉树的第i层最多有2-1个结点。(≥1) 证明用数学归纳法] 性质2深度为k的二叉树最少有k个结点, 最多有2k-1个结点。(k≥1) 因为每一层最少要有1个结点,因此,最少 结点数为k。最多结点个数借助性质1:用 求等比级数前项和的公式 20+21+22+..+2k-1=2k-1 12
二叉树的性质 • 性质1 若二叉树结点的层次从 1 开始, 则在 二叉树的第 i 层最多有 2 i-1个结点。( i≥1) [证明用数学归纳法] • 性质2 深度为 k 的二叉树最少有 k 个结点, 最多有 2 k-1个结点。( k≥1 ) 因为每一层最少要有1个结点,因此,最少 结点数为 k。最多结点个数借助性质1:用 求等比级数前k项和的公式 2 0 +21 +22 + …+2k-1 = 2k-1 12

.性质3 对任何一棵二叉树,如果其叶结点有 n个,度为2的非叶结点有n2个,则有 no =n2+1 若设度为1的结点有n1个,总结点数为n, 总边数为e,则根据二叉树的定义 n notn+nz e=2n+n=n-1 因此,有n2+以=no+什h-1 n2=0-1→no=n2+1 13
• 性质3 对任何一棵二叉树,如果其叶结点有 n0 个, 度为 2 的非叶结点有 n2 个, 则有 n0=n2+1 若设度为 1 的结点有 n1 个,总结点数为n, 总边数为e,则根据二叉树的定义, n = n0+n1+n2 e = 2n2+n1 = n-1 因此,有 2n2+n1 = n0+n1+n2-1 n2 = n0-1 n0 = n2+1 13
定义1满二叉树(Full Binary Tree) 一深度为k的满二叉树是有2k-1个结点的二叉树。 定义2完全二叉树(Complete Binary Tree) 若设二叉树的深度为k,则共有k层。除第k 层外,其它各层(1~k-1)的结点数都达到最大 个数,第层从右向左连续缺若干结点,这就是 完全二叉树。 14
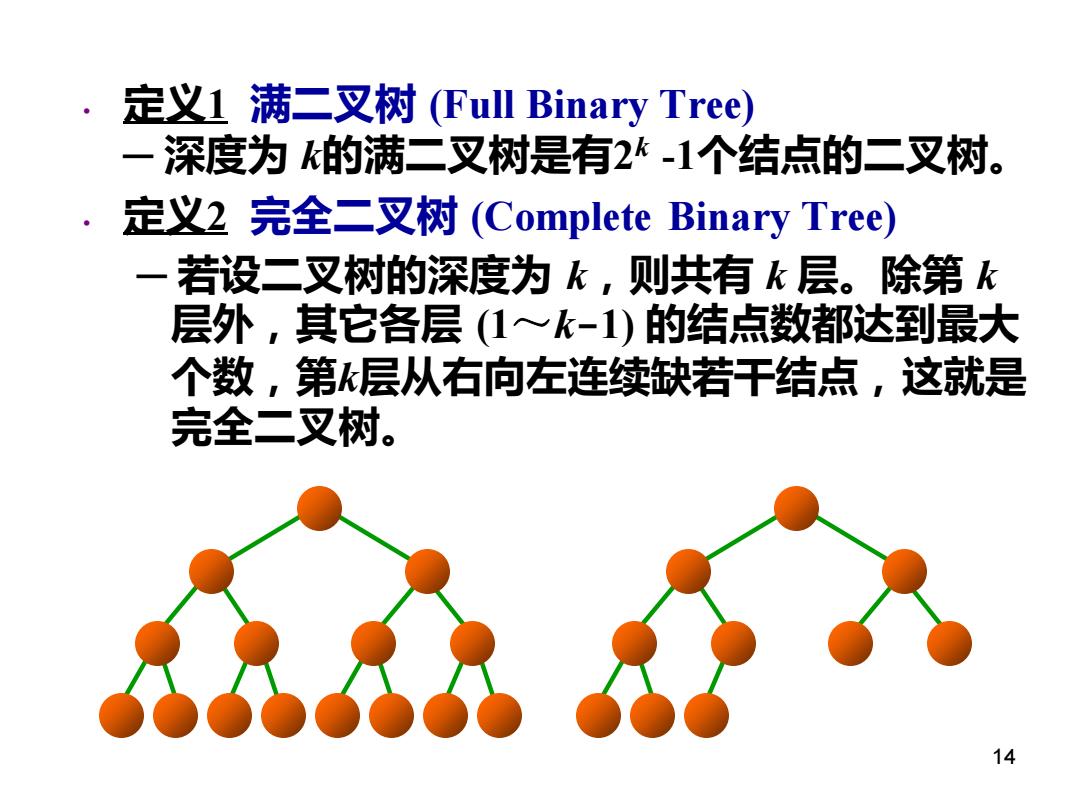
• 定义1 满二叉树 (Full Binary Tree) ─ 深度为 k的满二叉树是有2 k -1个结点的二叉树。 • 定义2 完全二叉树 (Complete Binary Tree) ─ 若设二叉树的深度为 k,则共有 k 层。除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大 个数,第k层从右向左连续缺若干结点,这就是 完全二叉树。 14

性质4具有n(n≥0)个结点的完全二叉树的 深度为「1og2(n+1)门 设完全二叉树的深度为k,则有 2<n≤2J 上面k-1层结点数 包括第k层的最大结点数 变形2k-1<n+1≤2k 取对数 231 k-1<log2(n+1)≤k 得到 , 1og2(+1)7=k 15
• 性质4 具有 n (n≥0) 个结点的完全二叉树的 深度为 log2 (n+1) 设完全二叉树的深度为k,则有 2 k-1-1 < n ≤ 2 k-1 变形 2 k-1 < n+1≤2 k 取对数 k-1< log2 (n+1) ≤k 得到 log2 (n+1) = k 上面k-1层结点数 包括第k层的最大结点数 2 3 -1 2 4 -1 15