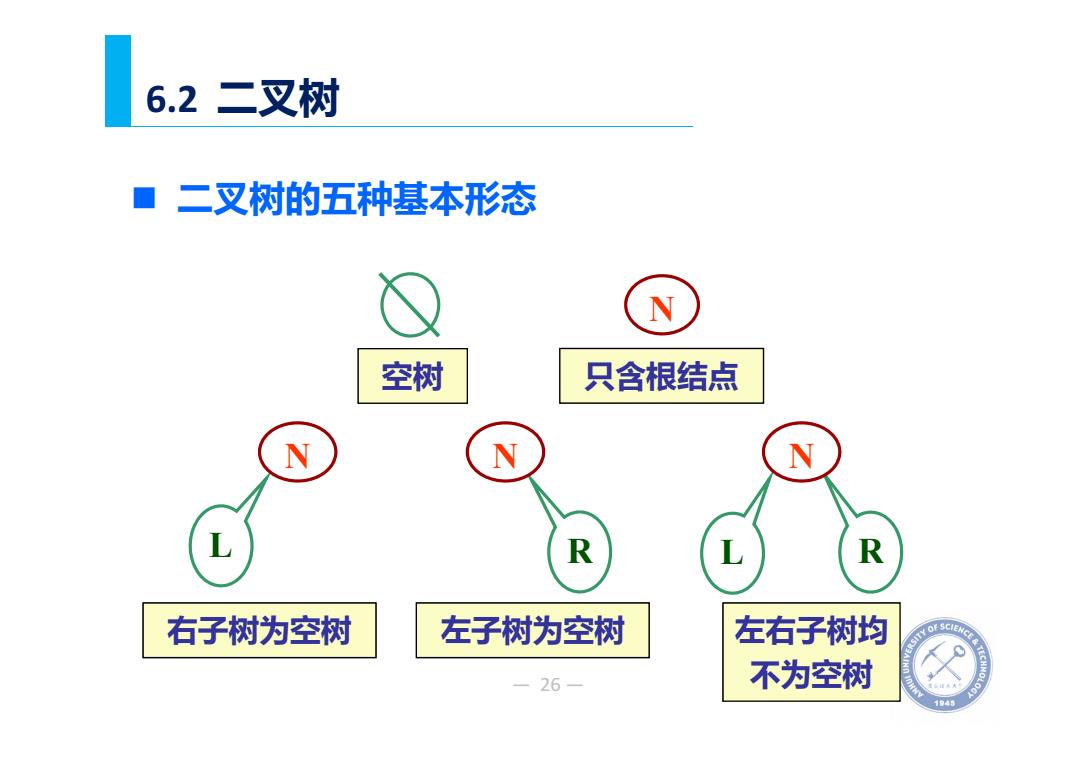
6.2二叉树 ■二叉树的五种基本形态 N 空树 只含根结点 N N N R R 右子树为空树 左子树为空树 左右子树均 -26 不为空树 1945
— 26 — 6.2 二叉树 二叉树的五种基本形态 N L R L R 空树 只含根结点 N N N 右子树为空树 左子树为空树 左右子树均 不为空树

6.2二叉树 6.2.2二叉树的性质 ■性质1:在二叉树的第i层上至多有21个结点(伦1)。 用归纳法证明: 归纳基:i=1层时,只有一个根结点: 2-1=20=1 归纳假设:假设对所有的j,1≤j<i,命题成立; 归纳证明:二叉树上每个结点至多有两棵子树, 则第i层的结点数=2-2×2=21 -27 1945
— 27 — 6.2 二叉树 用归纳法证明: 归纳基: 归纳假设: 归纳证明: i = 1 层时,只有一个根结点: 2i-1 = 20 = 1 假设对所有的 j,1≤ j i,命题成立; 二叉树上每个结点至多有两棵子树, 则第 i 层的结点数 = 2i-2 2 = 2i-1 6.2.2 二叉树的性质 性质1:在二叉树的第 i 层上至多有2i-1 个结点(i≥1)

6.2二叉树 6.2.2二叉树的性质 ■性质2:深度为k的二叉树上至多含2k-1个结 点21)。 证明:基于上一条性质,深度为k的二叉树上 的结点数至多为 20+2+.·,·..+2k-1=2k-1 -28 145
— 28 — 6.2 二叉树 性质2:深度为 k 的二叉树上至多含 2k-1 个结 点(k≥1)。 证明:基于上一条性质,深度为 k 的二叉树上 的结点数至多为 20+21+ +2k-1 = 2k-1 6.2.2 二叉树的性质

6.2二叉树 6.2.2二叉树的性质 性质3:对任何一棵二叉树,若它含有o个叶 子结点、2个度为2的结点,则必存在关系式: no=n2+l。 证明: 设二叉树上结点总数n=n,+n,+n2 又二叉树上分支总数b=n+2n2 而b=n-1=no+n1+n2-1 由此,n,=n2+1。 -29- 145
— 29 — 6.2 二叉树 证明: 设 二叉树上结点总数 n = n0 + n1 + n2 又 二叉树上分支总数 b = n1+2n2 而 b = n-1 = n0 + n1 + n2 - 1 由此, n0 = n2 + 1 。 性质3:对任何一棵二叉树,若它含有n0 个叶 子结点、n2 个度为 2 的结点,则必存在关系式: n0 = n2+1。 6.2.2 二叉树的性质
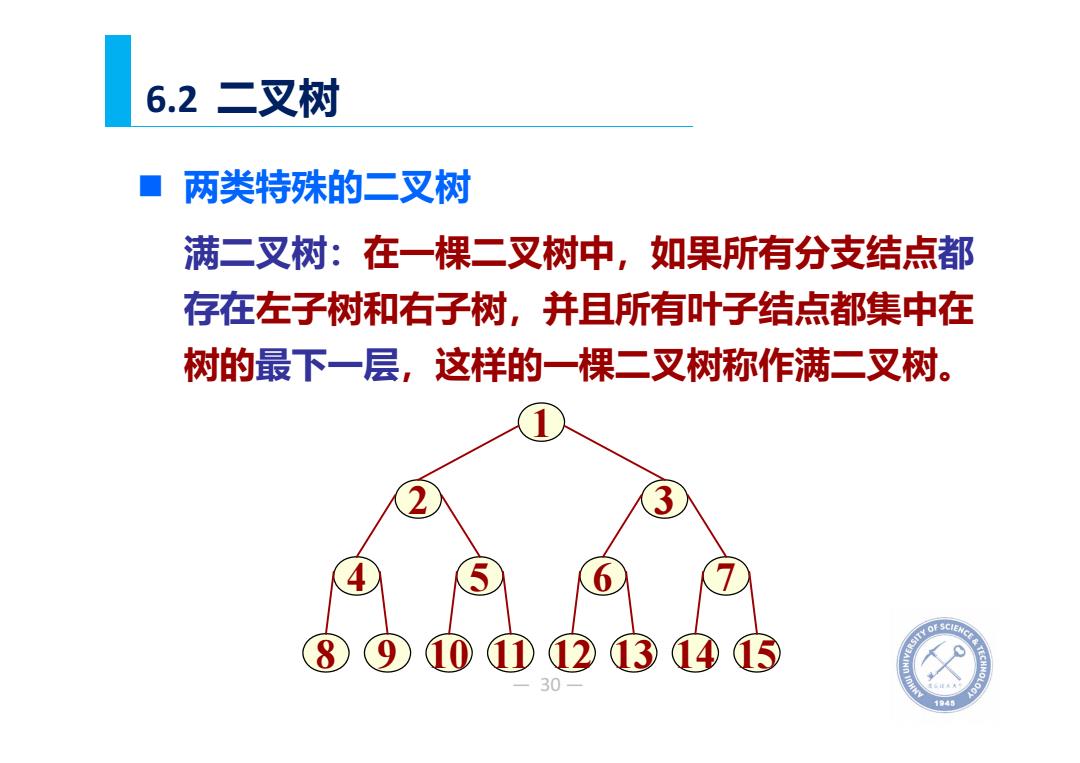
6.2二叉树 两类特殊的二叉树 满二叉树:在一棵二叉树中,如果所有分支结点都 存在左子树和右子树,并且所有叶子结点都集中在 树的最下一层,这样的一棵二叉树称作满二叉树。 12 1④ 15 1945
— 30 — 6.2 二叉树 两类特殊的二叉树 满二叉树:在一棵二叉树中,如果所有分支结点都 存在左子树和右子树,并且所有叶子结点都集中在 树的最下一层,这样的一棵二叉树称作满二叉树。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15