目录页 Contents Page 树的定义和基本术语 第六章 二叉树 树和二叉树 遍历二叉树和线索二叉树 树和森林 哈夫曼树及其应用 -6 1945
— 6— — 6— Contents Page 目录页 二叉树 遍历二叉树和线索二叉树 树的定义和基本术语 树和森林 哈夫曼树及其应用

6.1树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合,当 集合为空时称为空树,否则它满足如下两个条件: (1)有且仅有一个特定的称为根(Root)的结点; (2)其余的结点可分为m(m>=0)个互不相交的 子集T,T2Tm,其中每个子集又是一棵树,并称 为根的子树(Subtree)。 除根外每个结点有且仅有一个直接前驱,但可以 有0个或多个直接后继。 7 1945
— 7— 6.1 树的定义和基本术语 定义:树(Tree)是由n(n≥0)个数据元素的集合,当 集合为空时称为空树,否则它满足如下两个条件: (1) 有且仅有一个特定的称为根(Root)的结点; (2) 其余的结点可分为m(m>=0)个互不相交的 子集T1,T2…Tm,其中每个子集又是一棵树,并称 为根的子树(Subtree)。 除根外每个结点有且仅有一个直接前驱,但可以 有0个或多个直接后继
6.1树的定义和基本术语 A (a)空树 (b)仅含有根结点的树 根 T2={C,G} 子树加1= 根 (B,E,F,K,L) T3={D,H,I,J,0 (c)含有多个结点的树 1945
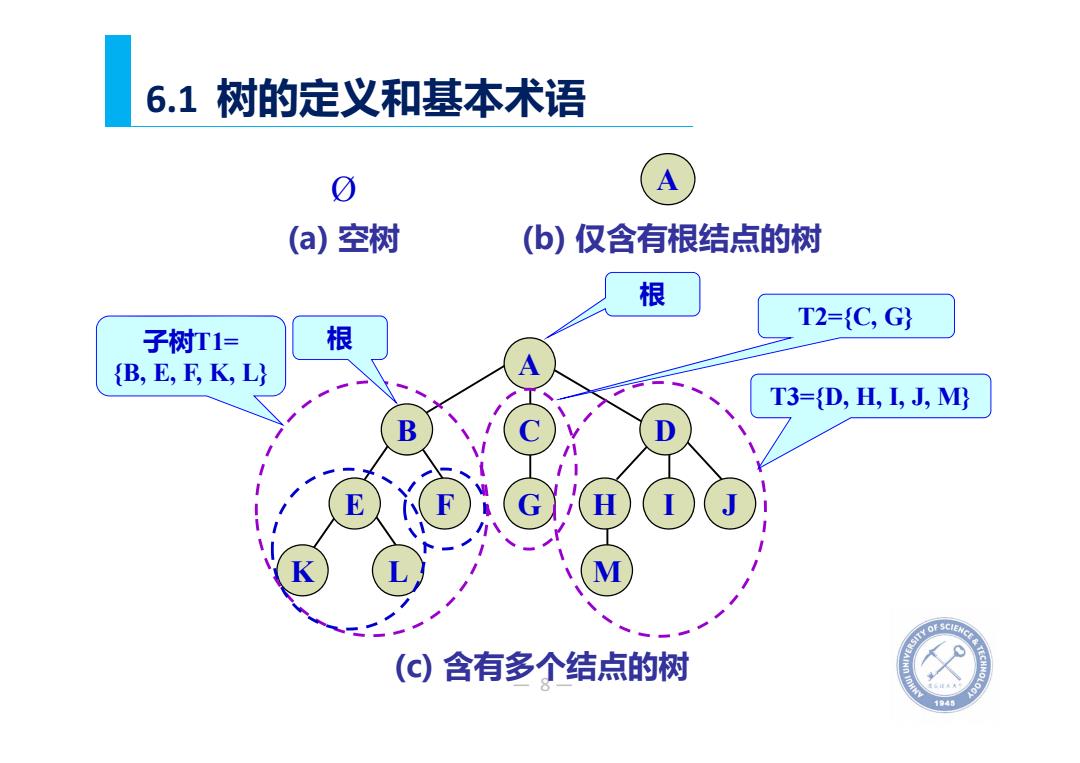
— 8— 6.1 树的定义和基本术语 Ø A (a) 空树 I J A B C D E F G H K L M (c) 含有多个结点的树 根 子树T1= {B, E, F, K, L} T2={C, G} T3={D, H, I, J, M} 根 (b) 仅含有根结点的树
6.1树的定义和基本术语 A ■树的逻辑结构特点: B C D F G H 1)树中只有根结点没有前趋: 2)除根外,其余结点都有且仅一个前趋: M 3)树的结点,可以有零个或多个后继; 4)除根外的其他结点,都存在唯一条从根到该结点 的路径; -9- 145
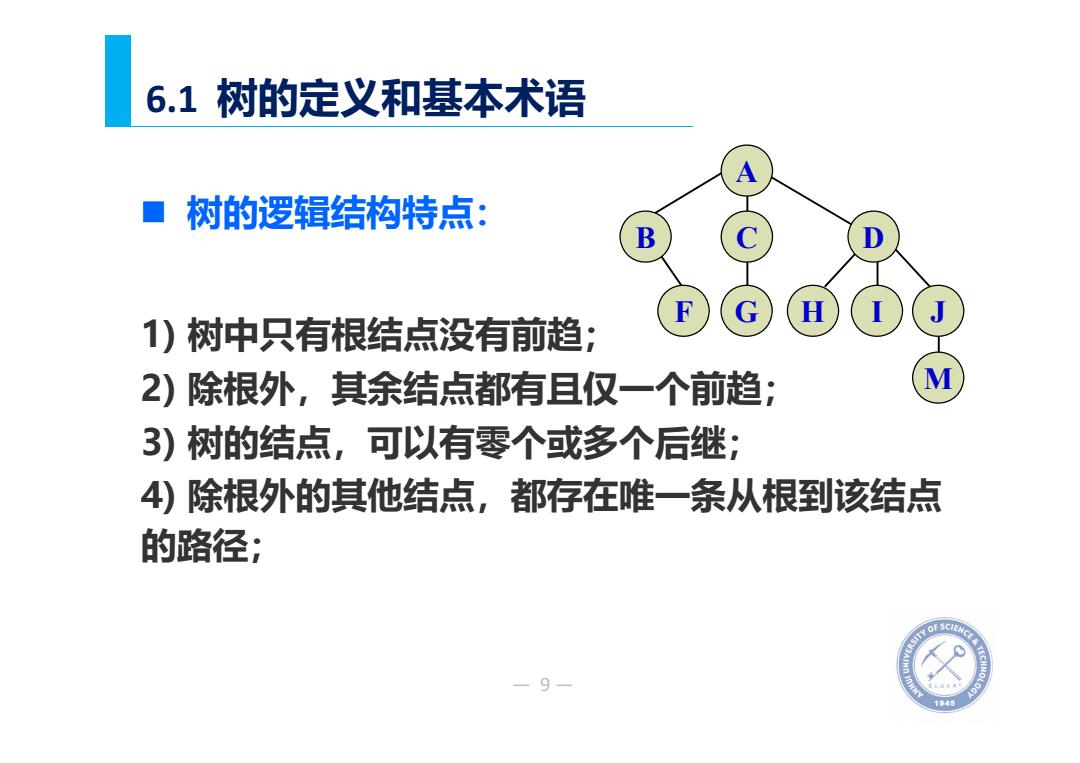
— 9— 6.1 树的定义和基本术语 1) 树中只有根结点没有前趋; 2) 除根外,其余结点都有且仅一个前趋; 3) 树的结点,可以有零个或多个后继; 4) 除根外的其他结点,都存在唯一条从根到该结点 的路径; 树的逻辑结构特点: I J A B C D F G H M

6.1树的定义和基本术语 ■树的表示 A B D 1.二元组表示法 E F G H K M K=A,B,C,D,E,F,G,H,LJ,K,L,MY R={r} ={<A,B>,<A,C>,<A,D>,<B,E>,<B,F>,<C,G> <D,H>,<D,>,<D,J>,<E,K>,<E,L>,<H,M>} -10 1945
— 10 — 6.1 树的定义和基本术语 K={A,B,C,D,E,F,G,H,I,J,K,L,M} R={r} r={<A,B>, <A,C>, <A,D>, <B,E>, <B,F>, <C,G>, <D,H>, <D,I>, <D,J>, <E,K>, <E,L>, <H,M>} 1. 二元组表示法 树的表示 I J A B C D E F G H K L M