
系统 热源3 热源2 热源1 若系统由状态A变化到状态B,可令系统与T热源接触, 则系统的环境温度由T立刻变为T1,热平衡时,向热源吸 热δQ1;接着更换T2热源,环境温度由T1立刻变为T2,热 平衡时,向热源吸热δQ2…。如此经过与多个热源接触, 系统由状态A变化到状态B
热源1 热源2 系 统 热源3 若系统由状态A变化到状态B,可令系统与T1热源接触, 则系统的环境温度由TA立刻变为T1,热平衡时,向热源吸 热δQ1;接着更换T2热源,环境温度由T1立刻变为T2,热 平衡时,向热源吸热δQ2… 。如此经过与多个热源接触, 系统由状态A变化到状态B

克劳修斯不等式 若A变化到B的过程不是可逆过程,则热温商之和为各矩形面积之和; 若过程可逆,则热温商之和等于A到B的曲线下围成的面积。 由熵的定义 d6= 62 T A到B的可逆过程熵变 △8,=R号 上式即为克劳修斯不等式。 δQ
1 / T A B δQ 2 3 1 4 若A变化到B的过程不是可逆过程,则热温商之和为各矩形面积之和; 若过程可逆,则热温商之和等于A到B的曲线下围成的面积。 A到B的可逆过程熵变 上式即为克劳修斯不等式。 由熵的定义 克劳修斯不等式
循环过程的熵变 若从A可逆变化到B,之后又由B可逆变化到A,则完 成了一个循环,此时总熵变 -+ =0 若从A不可逆变化到B,之后由B可逆变化到A,此循环是不 可逆过程,但总熵变仍然为零。不过总熵变不等于不可逆 循环的热温商之和,而是大于不可逆循环的热温商之和, 即 s-2+%>+9 +<0 循环过程可逆热温商之和为零, 而不可逆热温商之和小于零
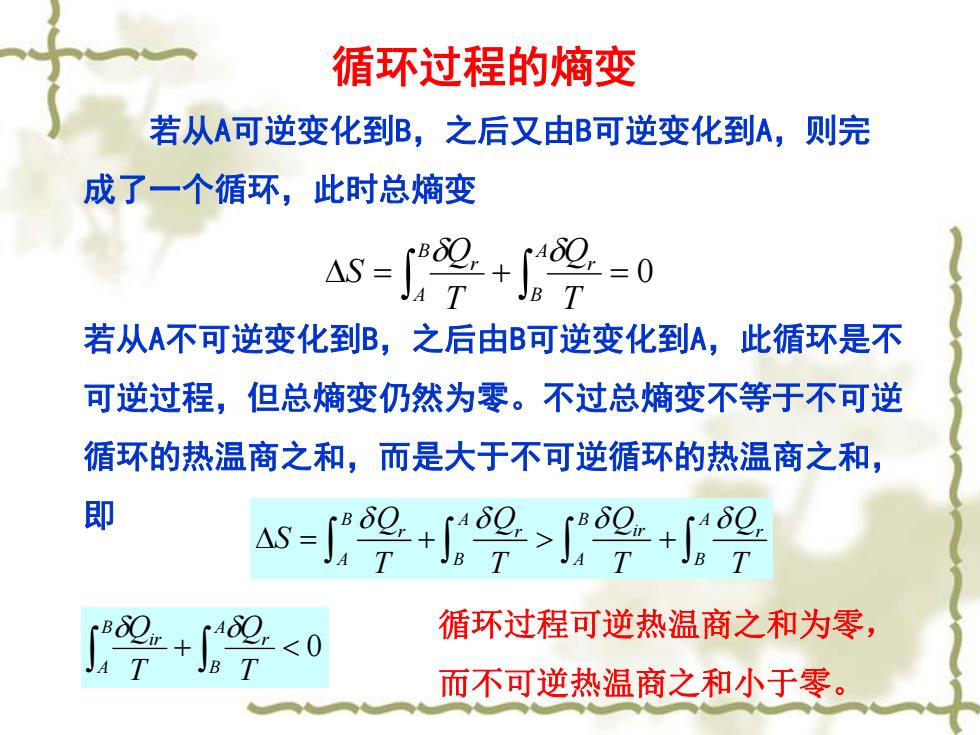
循环过程的熵变 若从A可逆变化到B,之后又由B可逆变化到A,则完 成了一个循环,此时总熵变 0 A B r B A r T Q T Q S 若从A不可逆变化到B,之后由B可逆变化到A,此循环是不 可逆过程,但总熵变仍然为零。不过总熵变不等于不可逆 循环的热温商之和,而是大于不可逆循环的热温商之和, 即 B A B A r r ir r A B A B Q Q Q Q S T T T T 0 A B r B A ir T Q T Q 循环过程可逆热温商之和为零, 而不可逆热温商之和小于零

熵所度量的是能量的退化、耗散或稀释 的程度,它使做功的能耐减小。世界的能量 若维持不变,但能量的可用度会随着世界熵 值的增加而越来越小。总之,若能量是系统 做功的能耐,熵就是这个能耐的贬值
熵所度量的是能量的退化、耗散或稀释 的程度,它使做功的能耐减小。世界的能量 若维持不变,但能量的可用度会随着世界熵 值的增加而越来越小。总之,若能量是系统 做功的能耐,熵就是这个能耐的贬值

S=kIn P 波兹曼首先找到熵和几率的关系式。系 统处于某一状态时的嫡,与系统处于该状态 的几率紧密相关。自发程序的熵增加,对应 系统从低几率状态到高几率状态的转移变化
波兹曼首先找到熵和几率的关系式。系 统处于某一状态时的熵,与系统处于该状态 的几率紧密相关。自发程序的熵增加,对应 系统从低几率状态到高几率状态的转移变化。 S k ln P