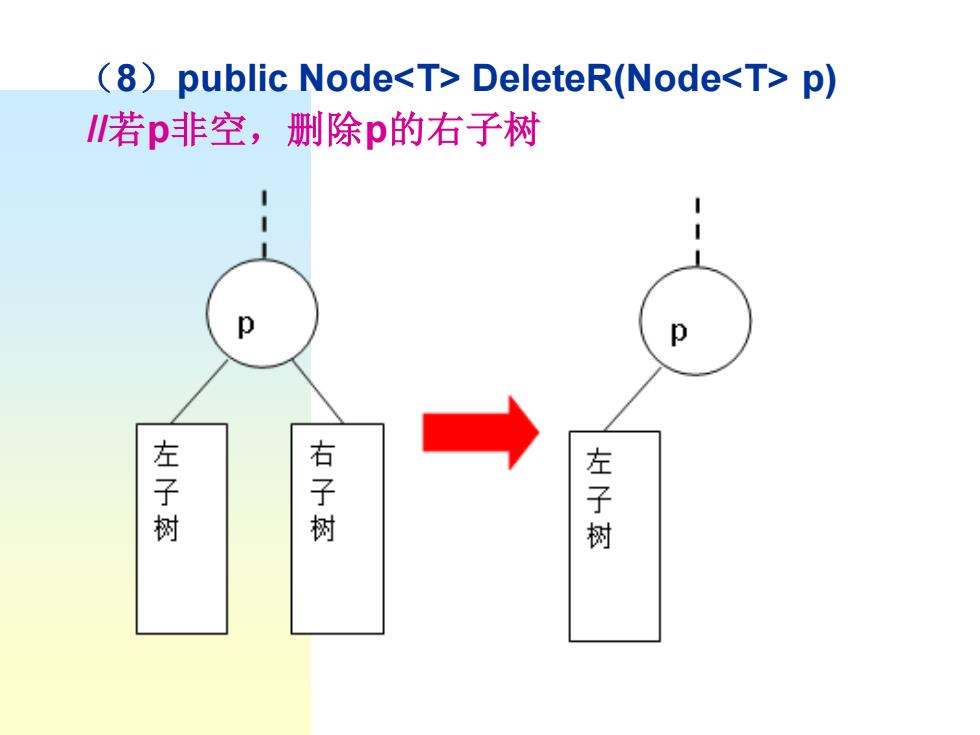
(8)public Node<T>DeleteR(Node<T>p) 若p非空,删除p的右子树 p p 左子树 右子树 左子树
(8)public Node<T> DeleteR(Node<T> p) //若p非空,删除p的右子树

(9)public bool IsLeaf(Node<T>p) 判断是否是叶子结点 (10)public void PreOrder(Node<T>root) 二叉树的前序遍历 (11)public void InOrder(Node<T>root) 二叉树的中序遍历 (12)public void PostOrder(Node<T>root) 二叉树的后序遍历 (13)public void LevelOrder(Node<T>root) 二叉树的层次遍历
(9)public bool IsLeaf(Node<T> p) //判断是否是叶子结点 (10)public void PreOrder(Node<T> root) //二叉树的前序遍历 (11)public void InOrder(Node<T> root) //二叉树的中序遍历 (12)public void PostOrder(Node<T> root) //二叉树的后序遍历 (13)public void LevelOrder(Node<T> root) //二叉树的层次遍历

6.2二叉树的性质 性质1若二叉树的层次从1开始,则在二叉树的第 i层最多有21个结点。(≥1) 证明:数学归纳法。 当i=1时,21=1二叉树的第1层上只有一个根结点。 第一层的结点数1<=21,所以命题成立。 假设=k时命题成立,即第k层上结点数目最多为21 当k+1时,第k+1层上结点数目最多为第k层上的两 倍,即2*2k-1=2k+11;命题也成立。 综上所述:命题成立
性质1 若二叉树的层次从1开始, 则在二叉树的第 i 层最多有 2 i-1个结点。(i 1) 证明:数学归纳法。 当i=1时, 2 i-1 =1; 二叉树的第1层上只有一个根结点。 第一层的结点数1<=2i-1,所以命题成立。 假设i=k时命题成立,即第k层上结点数目最多为2 k-1 当i=k+1时,第k+1层上结点数目最多为第k层上的两 倍,即2* 2k-1 =2k+1-1;命题也成立。 综上所述:命题成立。 6.2二叉树的性质

选择题: 在二叉树的第三层上最多有几个结 点()。 A.3B.4C.5D.6
选择题: 在二叉树的第三层上最多有几个结 点()。 A.3 B.4 C.5 D.6

性质2深度为k的二叉树最多有2k1个结点。(化≥1) 利用性质的结论每一层上具有的最大结点数如下表所示: 第层 k 围■sa■■ 3 2 每层结点数 2k-1 ■■■■■ 22 21 20 二叉树所具有的最大结点数: 2°+2+22++21=1-2 =2k-1 1-2
性质2 深度为k的二叉树最多有 2 k -1个结点。(k 1) 利用性质1的结论每一层上具有的最大结点数如下表所示: 第i层 k . 3 2 1 每层结点数 2 k-1 . 2 2 2 1 2 0 二叉树所具有的最大结点数: 2 1 1 2 1 2 2 2 2 . 2 k k 0 1 2 k 1 = − − − + + + + = −