
关于基本操作的几点说明: 1、基本操作是定义于逻辑结构上的基本操作,向外 界提供一个与其通讯的接口。还没有用具体的某种程 序语言写出具体的算法,而算法的实现只有在存储结 构确立之后。对应于不同的存储结构,树的基本操作 的实现也不相同。 2、基本操作的种类可随实际需要的不同而不同,定 义多少种基本操作由自己确定。 3、针对不同的需要,基本操作的参数和返回值可以 有所变化
关于基本操作的几点说明: 1、基本操作是定义于逻辑结构上的基本操作,向外 界提供一个与其通讯的接口。还没有用具体的某种程 序语言写出具体的算法,而算法的实现只有在存储结 构确立之后。对应于不同的存储结构,树的基本操作 的实现也不相同。 2、基本操作的种类可随实际需要的不同而不同,定 义多少种基本操作由自己确定。 3、针对不同的需要,基本操作的参数和返回值可以 有所变化

二叉树的基本操作: (1)public bool IsEmpty() 判断是否是空二叉树 (2)public Node<T>GetRoot() 获取根结点 (3)public Node<T>Getleftchild(Node<T>p) 获取结点的左孩子结点 (4)public Node<T>Getrightchild(Node<T>p) 获取结点的右孩子结点
二叉树的基本操作: (1)public bool IsEmpty() //判断是否是空二叉树 (2)public Node<T> GetRoot() //获取根结点 (3)public Node<T> Getleftchild(Node<T> p) //获取结点的左孩子结点 (4)public Node<T> Getrightchild(Node<T> p) //获取结点的右孩子结点

(5)public void InsertL(T val,Node<T>p) ∥将结点p的左子树插入值为val的新结点,原来的 左子树成为新结点的左子树 0 p val 右子树 左子树 右子树 左子
(5)public void InsertL(T val, Node<T> p) //将结点p的左子树插入值为val的新结点,原来的 左子树成为新结点的左子树

(6)public void InsertR(T val,Node<T>p) ∥将结点p的右子树插入值为val的新结点,原来的 右子树成为新结点的右子树 p 左子树 左子树 val 树 右子树
(6)public void InsertR(T val, Node<T> p) //将结点p的右子树插入值为val的新结点,原来的 右子树成为新结点的右子树
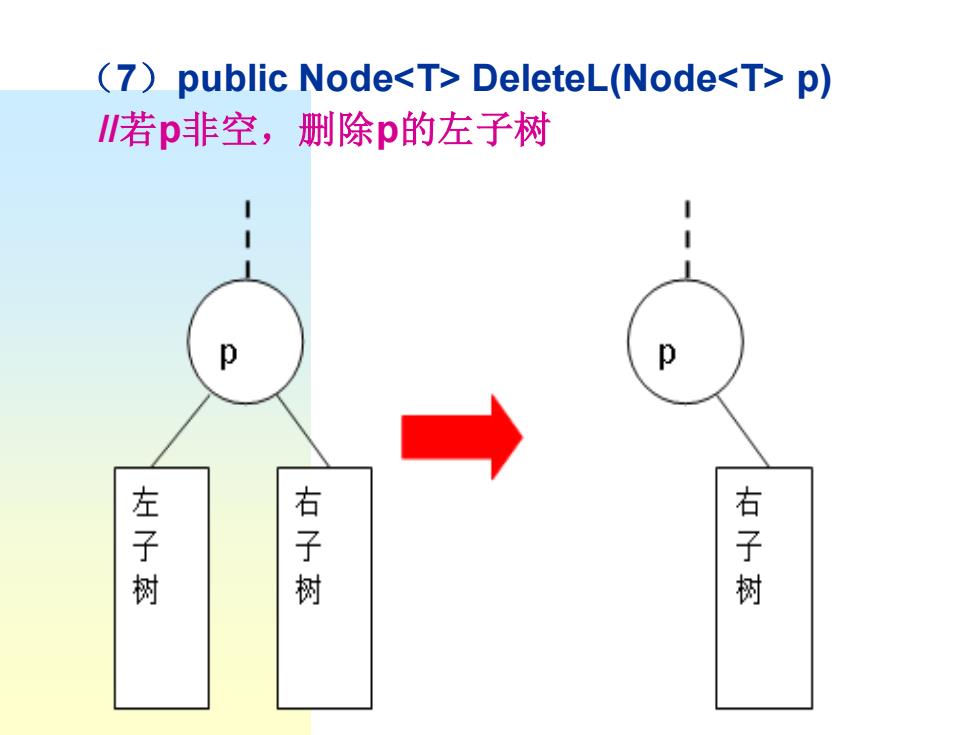
(7)public Node<T>DeleteL(Node<T>p) 若p非空,删除p的左子树 p p 左子树 右子树 右子树
(7)public Node<T> DeleteL(Node<T> p) //若p非空,删除p的左子树