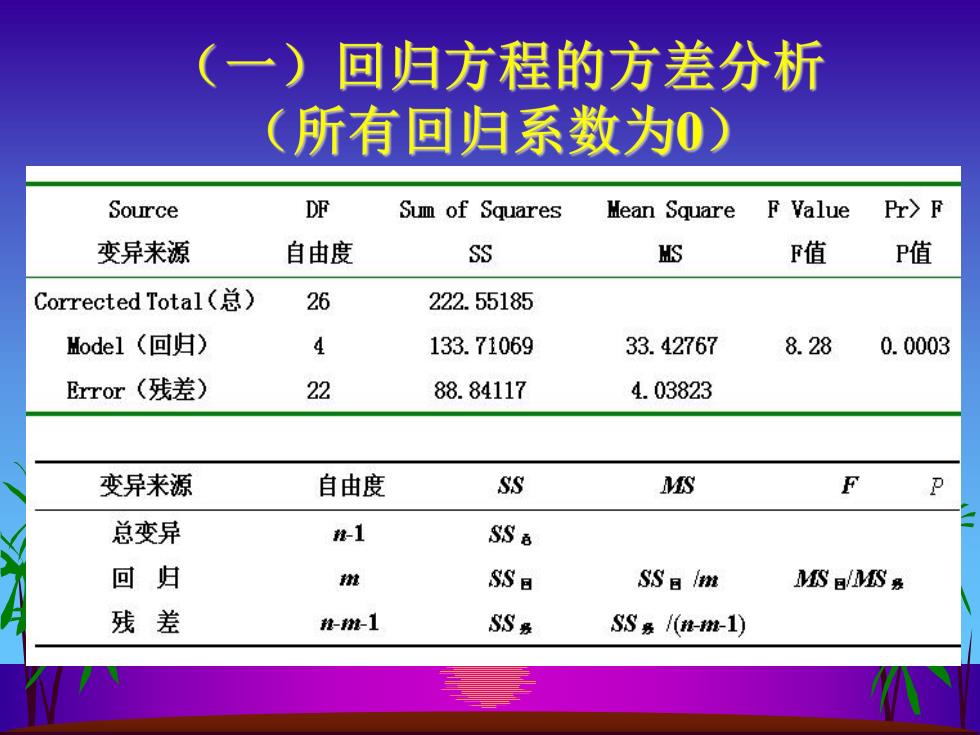
(一)回归方程的方差分析 (所有回归系数为0) Source DF Sum of Squares Mean Square F Value Pr>F 变异来源 自由度 SS HS F值 P值 Corrected Total(总) 26 222.55185 Model(回归) 4 133.71069 33.42767 8.28 0.0003 Eror(残差) 22 88.84117 4.03823 变异来源 自由度 SS MS F 总变异 雅-1 SS8 回归 拉 SSe SS日m MS MS 残差 移-推-1 SSs SS景f(-批-1)

有关计算公式 总变异∑(Y-)2=SS总=SS▣+SS饿 回归∑(-T)2=SS包=blg+blr++bn1r=∑b,lr 残差∑(Y-)2=SS残=SS总-SS回 用统计量F检验假设Ho:B,=B2=.=Bm=0是否成立 F= SS▣/m MS回 F心F(m,n-m-1) SS袋/(n-m-1) MS我

(二)有关评价指标

Root MSE (残差标准差) 2.00954 R-Square (决定系数) 0.6008 Adj R-Sq (校正决定系数) 0.5282 Dependent Mean 应变量的均值=11.92593
Root MSE (残差标准差) 2.00954 R-Square (决定系数) 0.6008 Adj R-Sq (校正决定系数) 0.5282 Dependent Mean 应变量的均值=11.92593

Root MSE 反映了回归方程的精度,其值越小说明回归 效果越好 4.0382 2.0095 1 ) /( 1) ˆ ( 2 ,12. SS残(n m ) MS残 SY m Y Y n m
Root MSE 反映了回归方程的精度,其值越小说明回归 效果越好 4.0382 2.0095 1 ) /( 1) ˆ ( 2 ,12. SS残(n m ) MS残 SY m Y Y n m