6.4.2.2㶲与理想功的异同 始态1 终态2 Wid 基态 x2 AE=E2-E=(H2-H)-T(S2-S)=Wid .理想功是终态与始态㶲的差值 惟真帷實
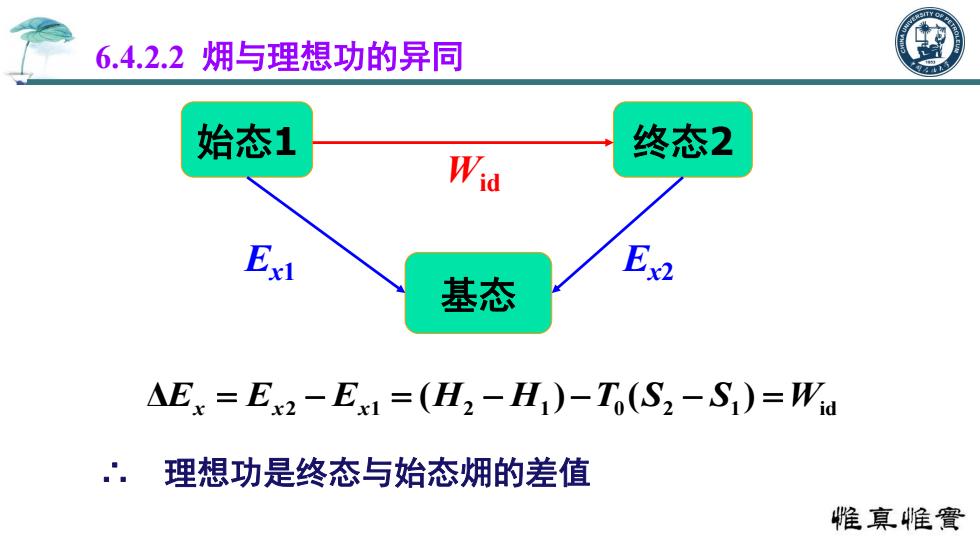
6.4.2.2 㶲与理想功的异同 始态1 终态2 基态 Wid Ex1 Ex2 2 1 2 1 0 2 1 id ΔEx Ex Ex (H H )T (S S ) W ∴ 理想功是终态与始态㶲的差值

6.4.2 稳流过程㶲计算 6.4.2.3物理㶲的计算 ◆定义:指物系由于T、p与环境的T,、po不同所具有 的做功能力。 ◆物理死态(约束性死态): 般取环境状态T,=25℃(298.15K) Po=latm (101.325 kPa) ◆当体系处于环境状态(To、Po)时,Ex=0 惟真帷竇
6.4.2.3 物理㶲的计算 定义:指物系由于T、p与环境的T0、p0不同所具有 的做功能力。 物理死态(约束性死态): 一般取环境状态T0 =25℃(298.15K) p0 =1atm (101.325 kPa) 当体系处于环境状态(T0、p0 )时,Ex =0 6.4.2 稳流过程㶲计算

几种常见情况的㶲计算 ◆)功、电能和机械能的㶲 —本身的数值 ◆2)热量烟Ex0 热量相对于基准态所具有的最大做功能力即为热 量㶲(热的有效能) 。 按Carnot循环所转化的最大功来计算。 惟真帷實
1) 功、电能和机械能的㶲——本身的数值 2) 热量㶲Ex,Q 热量相对于基准态所具有的最大做功能力即为热 量㶲 (热的有效能)。 按Carnot循环所转化的最大功来计算。 几种常见情况的㶲计算

对恒温热源,其热量㶲为 (6-31) 对变温热源(如由T变到T),其热量㶲为: .-o- (6-32) 式中Tm为热力学平均温度。T=-, 惟真帷竇
对恒温热源,其热量㶲为 m x Q T T E Q 0 , 1 (6-31) (6-32) T T Ex Q Q 0 , 1 0 , m 1 x Q T E Q T 对变温热源(如由T1变到T2 ),其热量㶲为: 式中Tm为热力学平均温度。 2 1 m 2 1 ln T T T T T

对于仅有显热变化的情况,如温度由T变到T。 Es.=(H-H)-T(S-So) -以c,ar-x7n B.eC-n 2d7 (6-34) 惟真帷竇
对于仅有显热变化的情况,如温度由T 变到T0 T T p T T p x Q T T C C T T E H H T S S 0 , 0 0 0 0 0 d d ( ) ( ) (6-34) T T p T T x Q p T T C E , C T T0 0 0 d d