
第2章燃烧与热化学 -祭器 (2.19) 这个方程假设液体相的比容与蒸气相比较是可以忽略的,且蒸气相的行为是理想气体。 例如,如果假设h是常数,对式(2.19)从(P1,T,)积分到(P.2,T2),就可以在已知 P1,T和Ta.2的条件下计算出P.2。我们将在液滴蒸发(第3章)和燃烧(第10章)中 采用这一方法。 2.3热力学第一定律 2.3.1第一定律一定质量 热力学第一定律表达的最基本的原理是能量守恒。对于一个质量一定的系统(图2.3(a), 能量守恒表示为在两个状态1和2之间的有限变化: 从状西1损软去品人背集一以款志系秋则风福的因一以款有男合接的安化 (2.20 定质量系统边界 控制体界面 控制体 m(e+Pu), L=0+m(e+P λ口2w 形,出口 (a 6 图2.3()带有活塞运动边界的定质量系统图示,(b)固定边界与稳定流动的控制体。 ,Q和W2都是路径函数,只发生在系统的边界上。△E1-2(=E,一E)是系统总能的 变化,总能是指内能、动能和势能的总和,即 E=mu+号v2+g (2.21) 系纯比质量内能暴统比质量动能系统比质最势能 系统的能量是一个状态参数,即△E与状态发生变化的路径无关。式(2.20)可以转化 为以单位质量为基准的形式或表示为随时刻变化瞬时量的形式,分别为 1q2-12=△e1-2-e2-e1 (2.22) 和 装系装人尚品时调支我幸一系烧对米整功家空。力的时得变北丰一属装出要化本 (2.23) q-w=de/dt (2.24)

式中,小写字母表示是比质量的参数,即e=E/m。 2.3.2第一定律一控制体 考虑如图2.3(b)所示的一个控制体,流体可以通过其边界流动。根据本书的目的,第 一定律的稳态稳定流动(SSSF)形式显得特别有用。读者在以前的热力学2~)学习中应该 已经相当熟悉。考虑到其重要性,下面简单地讨论一下。SSSF第一定律表示为 (2.25) 式中,下标0和i分别表示出口和人口,m是质量流量。在对式(2.25)写成更方便的形式之 前,先列出下面的一些体现在这一关系式中的基本假设: (1)控制体相对于坐标系是固定的。这就可以不考虑由于有运动边界而产生相互影响 的功,同时也可以不考虑控制体本身的动能和势能的变化。 (2)控制体内及控制面上的每一点的流体参数都不随时间变化。这一假设使我们处理 的所有过程都是稳态的。 (3)在入口和出口流动面上的流体参数都是均匀的。这样在人口和出口面上就不必进 行积分,而只需采用一个值来表示。 (4)只存在一个人口和一个出口。采用这一假设是为了使最终的结果具有简单的形 式。实际上这一假设可以很容易地放宽到多出/入口的情形。 人口和出口流体的比能e由比内能、动能和势能组成,即 单位二单位黄的内十 v2+ (2.26) 单位资址的动能 式中,V和z分别是流体流过控制面时的速度和高度。 式(2.25)中的压力-比容乘积项与流动功一起再与式(2.26)中的比内能结合,就是我 们所知道的得以广泛应用的参数格: h=u+Pv=u+P/p (2.27) 将式(2.25)一式(2.27)结合,并重新整理,就得到了控制体的最终能量守恒方程形式,即 Q。-m,=m[h。-h:)+2(-)+g(。-z)] (2.28) 将式(2.28)除以质量流量m,可以得到比质量下的第一定律表达式为 gw-=(h。-h)+(-)+g(x。-名) (2.29) 第?7章将引入能量守恒关系的更完整的形式,并在本书后续的使用中加以简化。目前 来讲,式(2.28)就够用了

第2章燃烧与热化学 2.4反应物和生成物的混合物 2.4.1化学计量学 氧化剂的化学当量值是刚好完全燃烧一定量的燃料所需要的氧化剂的量。如果提供的 氧化剂量超过了化学当量值,混合物被称为贫燃料,或者称为贫混合物;当提供的氧化剂量 少于化学当量值时,则称为富燃料或富混合物。假设燃料的反应形成一组理想的产物,氧化 剂(或空气)燃料的化学当量比(质量)简单地可由原子平衡来计算。对于碳氢燃料C,H, 化学计量关系式为 C.H+a(O2+3.76N2)→xCO2+(y/2)H2O+3.76aN2 (2.30) 式中, a=x+y/4 (2.31) 为简单起见,在全书,我们简单的假设空气是由21%的氧气和79%的氮气所组成(体积百分 比),即每1mol氧气的空气中,有3.76mol的氨气。 化学当量的空-燃比可表示为 a/Ps=()=76eMw 1 MWie (2.32) 式中,MW,和MWm分别为空气和燃料的摩尔质量。表2.1给出了甲烷和固体碳的化学 当量空-燃比。表中还给出了氢气在纯氧中燃烧时的氧-燃比。对所有的系统,我们发现氧 化剂都要比燃料多许多倍。 表2.1甲烷、氢气和固体碳在反应物温度为298K时的一些燃烧特性 Ahw.t/(kJ/kg) Aha.-/(kJ/kg) (O/F)/(kg/kg) T/K CH,十空气 -55528 -3066 17.11 2226 H,+0, -142919 -15880 8.0 3079 C(周)+空气 -32794 -2645 11.4 2301 ①O/F是氧化剂燃料比,当在空气中燃烧时,氧化剂是空气面不仅是指空气中的氧】 当量比Φ,常被用来定量地表示燃料-氧化剂混合物是富、贫或化学当量的。当量比定义为 中=2=A F/A A/F (2.33a) 从这一定义式可知,对于富燃料混合物,Φ>1;对于贫燃料混合物,Φ<1;对于化学当 量下的混合物,Φ=1。在许多燃烧应用中,当量比是单一最重要的确定系统性能的因素。 另一个常用来定义相对化学计量的参数是当量空气百分比。它与当量比的关系是

当量空气百分比=10g4 (2.33b) 与过量空气百分比 过量空气百分比=1。×100% (2.33c) 【例2.1】一小型低污染的固定燃气轮机发动机(如图2.4所示),在满负荷下运行 (3950kW),其当量比为0.286,空气的流量为15.9kg/5。燃料(天然气)的当量组成为 C.16H.。求燃料的质量流量和发动机的运行空-燃比。 解已知:币=0.286,MW=28.85,mm=15.9kg/5,MW=1.16×12.01+4.32× 1.008=18.286. 求:m阳和(A/F)。 我们先求(A/F),再求m。用定义式(2.32)和式(2.33)就可求解,即 (A/F)4.76aw 式中,a=x+y/4=1.16+4.32/4=2.24。故 一次风 旋流器 燃烧商 (a) (b) 图2.4()实验用的低氨氧化物燃气轮机燃烧筒;(b)(c)燃料与空气混合系统。(在一个 395okW的发动机中共采用8个燃烧简。资料来源:©1987,Electric Power Research Institute,EPRI AP-5347,Reduction for Small Gas Turbine Power Plants,允许复制)
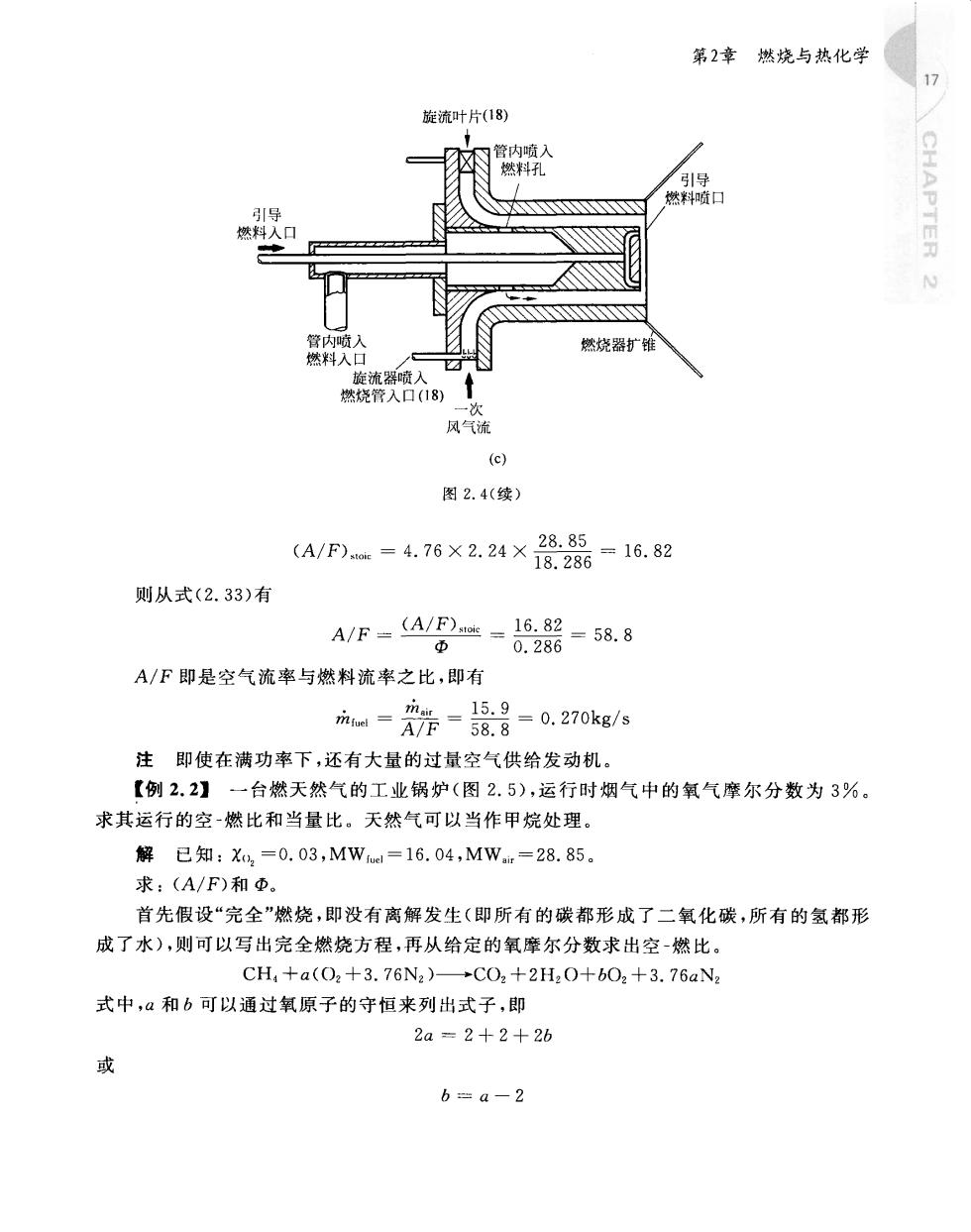
第2章燃烧与热化学 1> 旋流叶片(18) ☑衣N管内喷入 燃料孔 引导 CHAPTER N 3NN38NN 燃烧器扩推 风气流 (c) 图2.4(续) a/P=476X224×02器=16.82 则从式(2.33)有 A/F=A=2器=58.8 A/F即是空气流率与燃料流率之比,即有 m=8元=8-8=0.270kg/6 注即使在满功率下,还有大量的过量空气供给发动机。 【例2.2】一台燃天然气的工业锅炉(图25),运行时烟气中的氧气摩尔分数为3%。 求其运行的空-燃比和当量比。天然气可以当作甲烷处理。 解已知:X,=0.03,MW1=16.04,MWm=28.85。 求:(A/F)和D。 首先假设“完全”燃烧,即没有离解发生(即所有的碳都形成了二氧化碳,所有的氢都形 成了水),则可以写出完全燃烧方程,再从给定的氧摩尔分数求出空燃比 CH+a(O2+3.76N2)+CO2+2H20+b02+3.76aN2 式中,a和b可以通过氧原子的守恒来列出式子,即 2a=2+2+2b b=a-2