
燃烧与热化学 第 2 2.1概述 章 本章将仔细考察对于燃烧学习十分重要的几个热力学概念。首先,回 顾一下理想气体及其混合物的基本参数关系式和热力学第一定律。也许 这些概念在以前热力学的学习中读者已经熟悉,在本书列出来是因为它们 是燃烧学习完整的环节之一。本章后面将集中在与燃烧和反应系统相关 的热力学问题上:元素守恒相关的概念和定义;表征化学键能的焓的定 义;定义反应热、热值等的第一定律概念;绝热燃烧温度。还将导出基于 热力学第二定律概念的化学平衡,并应用于对燃烧产生的混合物的预测。 在此特别强调平衡的概念是因为对于许多实际的燃烧设备来说,平衡态的 知识就足以来定义许多设备的性能参数。例如,稳定流动的燃烧器的出口 温度和主要组成是由平衡决定的。本章还给出了一些例子来说明这些 原理。 2.2热力学性质关系式回顾 2.2.1广延量和强度量 广延量的数值取决于物质的数量(质量或物质的量)。广延量通常用 大写字母来表示,体积为V(m),内能为U(J),焓为H(J)(=U+PV)等。 另一方面,强度量以单位质量(或物质的量)来表示,它的数值与物质的数 量无关。基于单位质量的强度量一般用小写字母来表示,例如,比容为 (m3/kg),比内能为u(J/kg),比焙为h(J/kg)(=u十P)等。这一用小写 字母表示的规定有两个例外,就是强度量温度T和压力P。为区别起见, 基于单位物质的量的强度量在本书中用上画线来表示,如u和五(J/kmol) 从强度量得到广延量,只要简单地用单位质量(或物质的量)的值乘以物质 的质量(或物质的量),即 V=mw(或No) U=mu(或Nu) (2.1) H=mh(或Nh)

第2章燃烧与热化学 在下面的推导中,根据特殊的情况选择合适的量,既会用到基于质量的,也会用到基于物质 的量的强度量。 2.2.2状态方程 状态方程用来表示一种物质的压力P,温度T和体积V(比容积)之间的关系。对于 理想气体,即忽略分子间的作用力和分子体积的气体,状态方程可以表达成以下几种等效的 形式: PV=NR.T (2.2a) PV =mRT (2.2b) Pu=RT (2.2c) P=ORT (2.2d) 式中,气体常数R可以用通用气体常数R。和气体摩尔质量MW表示,即 R=R./MW (2.3) 式(2.2d)中的密度p是比容的倒数(p=1/~=m/W)。本书假设所有的气体组分和气体混合 物都具有理想气体的性质。这样的假设对于考虑的所有系统几乎都是合适的,因为燃烧所 产生的高温一般来说会形成足够低的密度,此时的理想气体是一个可接受的近似。 2.2.3状态的热方程 表示内能(或焙)与压力和温度关系的方程称为状态的热方程,即 u=u(T,v) (2.4a) h=h(T,P) (2.4b) 能量用单位cal来表示,在SI单位制中,用J来代替。 对式(2.4a)和式(2.4b)取微分,就可以获得u和h的微分的一般表达式,即 du=(器).dr+(),n (2.5a) ch -(dT+(),dP (2.5b) 上述两式中,对温度的偏导数相应是比定容热容和比定压热容,即 c,=(器) (2.6a) =()。 (2.6b) 对于理想气体,对比容的偏导数(au/au)r和对压力的偏导数(ah/P)r都为零。利用这一 点,将式(2.5)进行积分并将式(2.6)代人就获得了下列的理想气体状态的热方程:
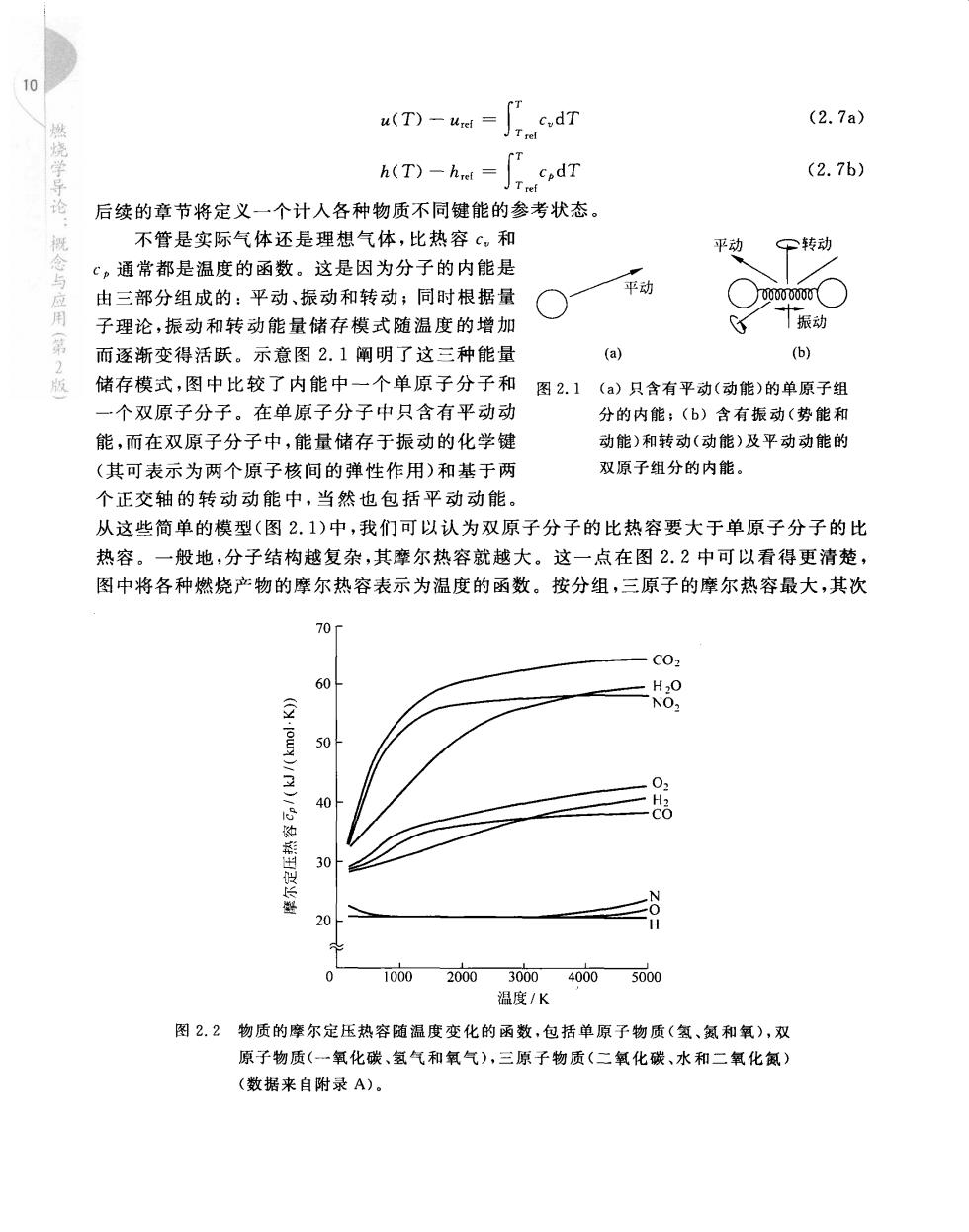
T--T (2.7a) A(T)-had -fr cdT (2.7b) 后续的章节将定义一个计人各种物质不同键能的参考状态。 不管是实际气体还是理想气体,比热容c,和 平动 转动 c。通常都是温度的函数。这是因为分子的内能是 由三部分组成的:平动、振动和转动;同时根据量 平动 子理论,振动和转动能量储存模式随温度的增加 振动 而逐渐变得活跃。示意图2.1阐明了这三种能量 (a 储存模式,图中比较了内能中一个单原子分子和 图2.1(a)只含有平动(动能)的单原子组 一个双原子分子。在单原子分子中只含有平动动 分的内能:(b)含有振动(势能和 能,而在双原子分子中,能最储存于振动的化学键 动能)和转动(动能)及平动动能的 (其可表示为两个原子核间的弹性作用)和基于两 双原子组分的内能 个正交轴的转动动能中,当然也包括平动动能。 从这些简单的模型(图2.1)中,我们可以认为双原子分子的比热容要大于单原子分子的比 热容。一般地,分子结构越复杂,其摩尔热容就越大。这一点在图2.2中可以看得更清楚, 图中将各种燃烧产物的摩尔热容表示为温度的函数。按分组,三原子的摩尔热容最大,其次 它 ·C0, 50 20 ∠8 0 10002000300040005000 温度K 图22物质的摩尔定压热容随温度变化的函数,包括单原子物质(氢、氨和氧),双 原子物质(一氧化碳、氢气和氧气),三原子物质(二氧化碳、水和二氧化氮) (数据来自附录A)

第2章燃烧与热化学 是双原子,最小的是单原子。从图2.2中还可以注意到,三原子分子随温度的变化也比双原 子分子要大,这是由于当温度升高过程中有更多的转动和振动模式变得活跃的缘故。相应 的,单原子分子则在相当宽的温度范围内摩尔热容近似为常数,事实上,从200K到5000K, 氢原子摩尔热容就是常数(G,=20.786kJ/(kmol·K))。 附录A中的表A.1~表A.12给出了各种物质摩尔定压热容随温度变化的函数。附录 A中还给出了相应拟合曲线的系数值。这些系数值取自CHEMKIN的热力学数据),数据 还用来生成了附录A中的表格。这些系数可以方便地用在电子表格软件来计算给定温度 范围内任意温度的c。值。 2.2.4理想气体混合物 用于表示混合物的组成的两个重要且有用的概念是组分摩尔分数和组分质量分数。考 虑一个多组分的混合物,其中组分1含有N,mol,组分2含有N2mol等,则组分i的摩尔分 数X,定义为i占系统总的物质的量的分数,即 名=N,+N+出十N十=心 N (2.8) 同样地,组分i的质量分数Y:就是i的质量占总混合物质量的份额,即 Y=m,十m十0十m十一 (2.9) 值得注意的是,根据定义,所有组分的摩尔(质量)分数的总和是1,即 ∑x=1 (2.10a) ∑Y,=1 (2.10b) 用物质i的摩尔质量和混合物的摩尔质量,就可以在摩尔分数和质量分数之间进行换 算,即 Y:=X.MW:/MW (2.11a) x.Y.MW/MW. (2.11b) 混合物的摩尔质量MW:可以很容易用物质的摩尔分数或质量分数来计算出,即 MWa=∑X,Mw, (2.12a) MW==∑Y,/Mw,) 1 (2.12b) 组分摩尔分数也可用来确定出对应组分的分压。组分i的分压卫指的是其在相同的温 度下从混合物中分离出来并占有全部混合物的体积时的压力。对于理想气体,混合物的压 力就是所有物质的分压之和,即

P=∑P (2.13) 分压则可用混合物成分的摩尔分数和总压来计算得到,即 P.X.P (2.14) 对于理想气体混合物,多数的以质量(或物质的量)为基的混合物强度参数可以简单地 用各物质的强度参数的质量分数(或摩尔分数)的加权和来计算得到。例如,混合物的焓为 ha=∑Yh, (2.15a) 万k=∑X:万, (2.15b) 其他用这种方法来处理的常用参数还有内能“和“。在理想气体的假设下,不管是纯 物质参数(u,u,h,九,),还是混合物的参数都与压力无关 混合物的熵也可以用各物质的加权和来计算: sm.(T,P)=∑Ys:(T,P,) (2.16a) 5k(T,P)=X:5,(T,P,) (2.16b) 不过此时,如式(2.16)所示,单一物质的熵(s和5)取决于该组分的分压。式(2.16)中 各组分的熵可以用标准状态(P=p一1atm)的值来计算,即 sT,R)=CT,P)-Rn品 (2.17a) 3.(T.P.)=3(T,Pu)--R.ln p P (2.17b 燃烧过程中常见的一些物质的标准状态下摩尔比熵在附录A中列出。 2.2.5蒸发潜热 在许多燃烧过程中,液体-蒸气之间的相变很重要。例如,一个液体燃料滴在燃烧之前 首先要蒸发;又如,如果充分冷却,燃烧产物中水蒸气会凝结。定义蒸发潜热:为在给定 温度下单位质量的液体在定压过程中完全蒸发所需要的热量,即, hi(T,P)=hvapor (T,P)-htouid (T,P) (2.18) 式中,T和P为相应的饱和温度和饱和压力。蒸发潜热又叫作蒸发焓。各种燃料在常压沸 点时的蒸发潜热在附录B表B.1中列出。 给定温度和压力下的蒸发潜热经常和克劳修斯-克拉珀龙(Clausius-Clapeyron)方程一 起用来计算饱和压力随温度的变化,即